相関係数／ピアソンの積率相関係数とは？：AI・機械学習の用語辞典

用語「相関係数（ピアソンの積率相関係数）」について説明。相関係数とは2つの変数間の関係の強さと方向性を表す、1〜0〜-1の範囲の数値。1（強い正の相関）では、2つの変数が強く同方向に連動する。-1（強い負の相関）では強く逆方向に連動する。相関なしでは、連動しない。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　数学／統計学／機械学習における相関係数（correlation coefficient）とは、2つの変数間の関係の強さと方向性（＝相関：correlation）を表す、1〜0〜-1の範囲の数値である。1に近い値は「強い正の相関」、つまり2つの変数が強く同方向に連動することを意味する。0.3など0に近くなるほど相関は弱まっていき、0に近い値は「相関なし」、つまり2つの変数が連動しないことを意味する。また、-1に近い値は「強い負の相関」、つまり2つの変数が強く逆方向に連動することを意味する。

　相関係数には主に、線形の（linear、直線的）相関を調べる標本相関係数（sample correlation coefficient）の、

• ピアソンの積率相関係数（PCC：Pearson Correlation Coefficient、PPMCC：Pearson Product-Moment Correlation Coefficient、Pearson's r）

と、非線形の（non-linear、曲線的）相関や、単調増加／減少関係の（monotonic）相関を調べる順位相関係数（rank correlation coefficient）の、

• スピアマンの順位相関係数（Spearman's rank correlation coefficient）
• ケンドールの順位相関係数（Kendall rank correlation coefficient、Kendall's τ coefficient）

の3種類がある。単に相関係数と言った場合、通常はピアソンの積率相関係数を指す。また、順位相関係数は2種類あるが、スピアマンの方がよく使われている。本稿では、ピアソンの積率相関係数（以下、単に「相関係数」）の内容を解説する。

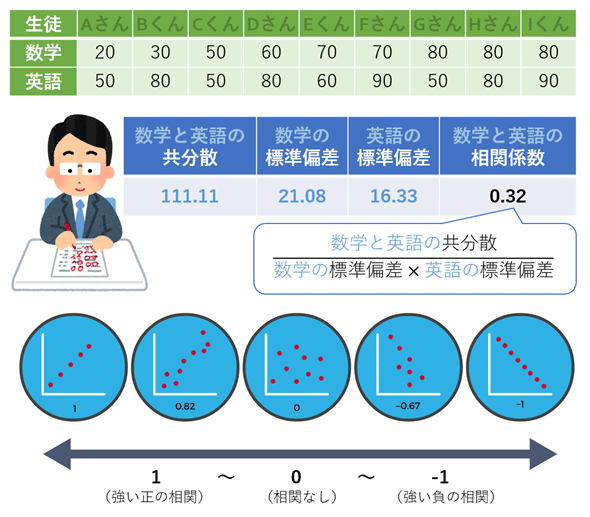図1　相関係数（ピアソンの積率相関係数）のイメージ
2つの変数で散布図を描くと相関係数は可視化できる。強い正の相関がある場合（つまり相関係数が1に近い場合）は、図のように右上がりの直線になり、強い負の相関関係がある場合（つまり相関係数が-1に近い場合）は、図のように右下がりの直線になる。相関がない場合（つまり相関係数が0に近い場合）は、図のように点がバラバラで直線が引けないような状態になる。ちなみに本稿では説明していないが、散布図で点の集まりが直線ではなく曲線になる場合は、ピアソンの積率相関係数よりも、スピアマンの順位相関係数の方が適している可能性がある。

相関係数（ピアソンの積率相関係数）の意味と求める方法

　「相関係数は、-1〜1の数値で、2つの変数間の関係の強さと方向性を表す」と言われても「具体的にどう計算されているかがイメージできない」という人も少なくないだろう。そこで相関について、もっと根本的なところから説明しておこう。

　例えば2つの変数xとyに「正／負の相関がある」「相関がない」というのがどういう状態を指すのかをイメージしてみてほしい。これらは次のような状態を指す。

• 正の相関がある： 変数xが大きくなると、変数yも同方向に連動して大きくなる状態
• 負の相関がある： 変数xが大きくなると、変数yが逆方向に連動して小さくなる状態
• 相関がない： 変数xが大きくなっても、変数yはそれに連動しては変化しない状態

　これを数式で表現するために、「変数xの大きさ」は、「変数xの平均値からの偏差（＝平均値を中心0にした場合の値、中心化した値）」で表現し、同様に「変数yの大きさ」は、「変数yの平均値からの偏差」で表現することにしよう。この場合、

• （変数xの偏差）×（変数yの偏差）

を計算すると、変数xの偏差と変数yの偏差がどちらも大きくて（＝関係の強さ）、プラス／マイナス（＝方向性）が一致している場合には、「大きな正の数値（＝強い正の相関）」になる。プラス／マイナスが一致しない場合には、「負の数値（＝負の相関）」になる。この計算を、全データに対して行って足し合わせた上でデータ数で割る（＝平均する）ことで、データ全体における相関が求められることになる。ここまでの計算は共分散（covariance）と呼ばれる。

　しかし共分散では、データセットによってスケール（単位）が異なる可能性があるので、「複数のデータセット間で、どの相関が強いか弱いか」といった比較ができないという欠点がある。この欠点を解消するためには、正規化を行う必要がある。相関係数では正規化の一種である標準化を行う。具体的には、変数xの偏差を標準化するために、共分散を変数xの標準偏差で割り、さらに変数yの偏差を標準化するために、共分散を変数yの標準偏差で割る。以上の計算によってスケールが1〜0〜-1の範囲に整うというわけである（表1は数値が持つ意味の目安）。

相関係数	相関の強さと方向性
0.7〜1.0	強い正の相関
0.4〜0.7	正の相関
0.2〜0.4	弱い正の相関
-0.2〜0.2	相関がない
-0.4〜-0.2	弱い負の相関
-0.7〜-0.4	負の相関
-1.0〜-0.7	強い負の相関
表1　相関係数の範囲と「相関の強さと方向性」の目安

因果関係と疑似相関に注意

　相関関係と因果関係は必ずしも一致しないことに注意してほしい。例えば「数学テスト」と「英語テスト」の相関が高いからといって、必ずしも「数学テスト」が高いから（原因）、「英語テスト」も高い（結果）という因果関係があるとは限らない。

　また、実際には相関がないにもかかわらず、見かけ上の相関（擬似相関）が数値に出る場合もあるので注意してほしい。例えば小学校全体でデータを取って「走る速さ」と「数学テスト」に高い相関が見られたとしても、必ずしも実際に相関があるとは限らない。この例では、「年齢」という潜在変数が両変数の間に隠れていることが考えられる。つまり実際には、「年齢」と「走る速さ」に高い相関があり、「年齢」と「数学テスト」にも高い相関があるために、あたかも「走る速さ」と「数学テスト」に高い相関があるように見えているだけということだ。

外れ値に注意しよう

　相関係数は、外れ値の影響を大きく受ける可能性があることに注意してほしい。例えば、あるクラスの生徒の「身長」と「数学テストの点数」に通常は相関関係が見られないはずだが、もし最も身長が高い生徒がたまたま最も高い点数を取っている場合、相関係数は実際よりも高くなる可能性がある。外れ値が計算結果に影響を与えていないかどうかをチェックするため、データを散布図や箱ひげ図で可視化し、データ全体のパターンを目視で確認することが重要だ。

データの分布と適切な相関係数の選択

　変数間の関係を正確に評価するためには、データの分布を考慮することも重要である。特に、ヒストグラムで描画したデータの分布が正規分布のように左右対称な山型になっていない場合、ピアソンの積率相関係数は適切な指標ではないことがある。例えば、所得と消費の関係を分析する際に、所得の分布が偏っている場合、ピアソンの積率相関係数は実際の関係を適切に反映しない。このような状況では、スピアマンの順位相関係数やケンドールの順位相関係数など、他の相関係数を用いることが推奨される。

「相関係数（ピアソンの積率相関係数）」の定義と数式

　相関係数（ピアソンの積率相関係数）の数式は、以下のように定義できる。上記の「相関係数（ピアソンの積率相関係数）の意味と求める方法」で説明した通りの計算式になっているが、データ数で割る1/nの計算は打ち消し合って全て消せるので、よりシンプルな式で表現できる。

「AI・機械学習の用語辞典」

ここを更新しました（2024年4月8日）

2024年4月8日：「データの分布と適切な相関係数の選択」という節を追記しました。
2023年11月6日：「外れ値に注意」という節を追記しました。