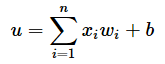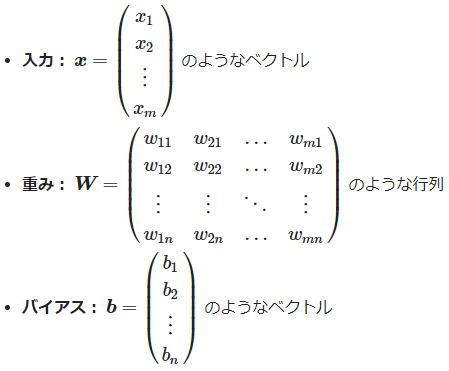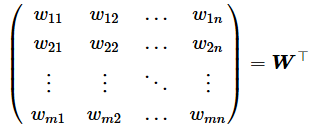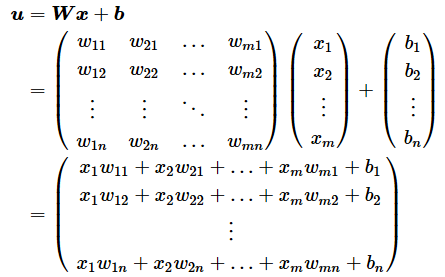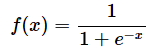NumPyでニューラルネットワークをフルスクラッチ実装してみよう:ニューラルネットワーク入門(1/3 ページ)
「線形代数を使ったニューラルネットワークの基礎を押さえたい!」という方にピッタリ。ニューラルネットワークをPython+NumPy(線形代数)でフルスクラッチ実装する。線形代数なしで実装した場合との差分から効率的に理解できる。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本連載(応用編)の目的
本連載(基礎編)の第1回〜第3回では、ディープラーニングに対応したニューラルネットワーク(DNN:Deep Neural Network、以下では「ニューラルネット」と表記)をスクラッチ(=他者が書いたソースコードを見たりライブラリーを使ったりせずに、何もないゼロの状態からコードを記述すること)で実装しました。その際、あえてNumPy、つまり線形代数を使わずにPythonのみを使用することで、数学の知識に自信がない人でもニューラルネットの処理/計算をステップ・バイ・ステップで追いかけられるようにしました。これにより、より多くの人が理解できたのではないかと思っています。
しかし、実際のニューラルネットワークの実装ではNumPy(線形代数)を使用することが一般的です。よって、より自信を持って、
- 「ニューラルネットや誤差逆伝播を完全に理解している」
- 「そらでコードが書ける」
- 「人に説明できる」
と言うためには、前回までの「Pythonのみ(線形代数なし)による実装」と、今回の「Python+NumPyによる実装」の違いを知り、実際にコーディングでそのギャップも埋めてみる必要もあるでしょう。今回はこれが目的となります。
また、基礎編ではできるだけ数式を使わずに説明しましたが、今回の応用編では図やコードだけでなく数式でも表現しました。これにより、コードと数学理論を結び付けて理解できるようになっていると思います。
本連載(応用編)のポイント
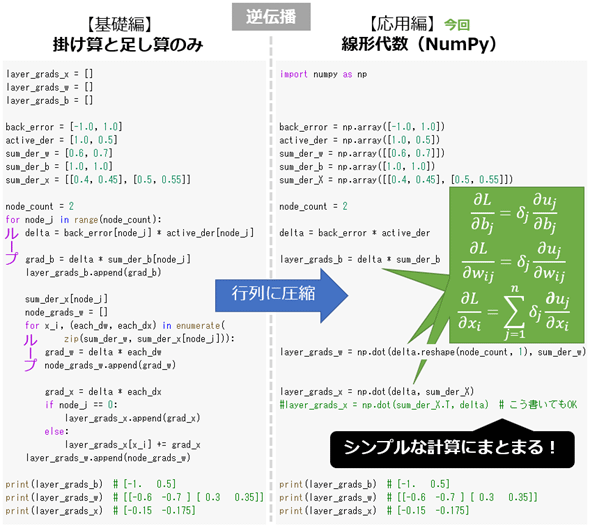
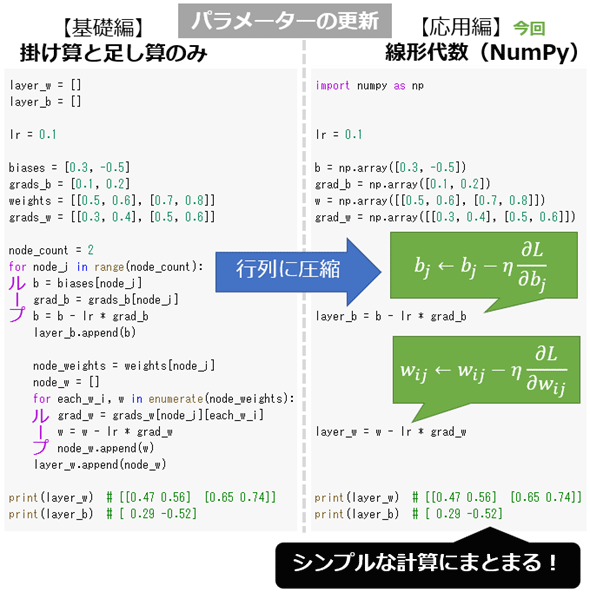
といっても、今回の内容はそれほど難しくありません。具体的には、forループを使っていた繰り返し処理部分のコードを、NumPyを使うコードに置き換えるだけにしています。基礎編でやったことの逆パターンですね(実際に図1は第1回で掲載した図1の左右を入れ替えただけの図です。※図1〜3に記載された数式の意味は後述します)。ただし入力データは、基礎編と同様にバッチサイズの行列(二次元配列)では扱わず、1件ずつのベクトル(一次元配列)で扱います(その分、よりシンプルな線形代数の計算式となっています)。
図1は順伝播における重み付き線形和の処理コードをNumPy化した場合の参考例となります。同様に、図2は逆伝播における勾配計算のコードを、図3は最適化におけるパラメーター更新のコードをNumPy化した場合の参考例です。
図2を見ると複雑なループ処理がたった4行のコードにまとめられています。前回は1つずつ計算しましたが、行列やNumPyを使えば今回のようにまとめて計算できます。
今回で説明したい重要ポイントは以上になります。ニューラルネットワークの仕組みや計算内容、実装方法は基礎編で解説済みです。繰り返しになりますが、今回はその基礎編においてforループで書いた計算の流れを線形代数やNumPyで表現していくだけの内容になります。
よって、計算内容の解説は線形代数/NumPyに関わること以外は基本的に割愛します。コードばかりが並ぶ記事になりますがご了承ください。仕組みや計算内容を再確認したい場合は、
を横に並べて本稿の記事を参照してください。比較しやすいように、コードの「リスト1」などの番号を一致させています。また、基礎編から変更した部分を太字にしています。
それでは、基礎編と同じ順でコードを掲載していきます。本稿の全体のコードを実行したい場合は、下記のリンク先のノートブックをご利用ください。
NumPyのインポート
今回はNumPyを利用するため、numpyモジュールをインポートします。
import numpy as np
ここからの内容に不明点がある場合は、「第1回:順伝播」も併せてご参照ください。
訓練(学習)処理全体の実装
今回の実装では、入力やパラメーター(重み/バイアス)、勾配などは、基本的にリスト値ではなくNumPyの多次元配列値(ndarray値)として扱うようにします。np.array(リスト値)という関数呼び出しで、リスト値を多次元配列値に変換できます。
# 取りあえず仮で、空の関数を定義して、コードが実行できるようにしておく
def forward_prop(cache_mode=False):
" 順伝播を行う関数。"
return None, None, None
y_true = np.array([1.0]) # 正解値
def back_prop(y_true, cached_outs, cached_sums):
" 逆伝播を行う関数。"
return None, None
LEARNING_RATE = 0.1 # 学習率(lr)
def update_params(grads_w, grads_b, lr=0.1):
" パラメーター(重みとバイアス)を更新する関数。"
return None, None
# ---ここまでは仮の実装。ここからが必要な実装---
# 訓練処理
y_pred, cached_outs, cached_sums = forward_prop(cache_mode=True) # (1)
grads_w, grads_b = back_prop(y_true, cached_outs, cached_sums) # (2)
weights, biases = update_params(grads_w, grads_b, LEARNING_RATE) # (3)
print(f'予測値:{y_pred}') # 予測値: None
print(f'正解値:{y_true}') # 正解値:[1.]
モデルの定義と、仮の訓練データ
入力層のノードが2個、隠れ層のノードが3個、出力層のノードが1個のモデル(model変数)を定義してみましょう。
# ニューラルネットワークは3層構成
layers = [
2, # 入力層の入力(特徴量)の数
3, # 隠れ層1のノード(ニューロン)の数
1] # 出力層のノードの数
# 重みとバイアスの初期値
weights = [
np.array([[0.0, 0.0], [0.0, 0.0], [0.0, 0.0]]), # 入力層→隠れ層1
np.array([[0.0, 0.0, 0.0]]) # 隠れ層1→出力層
]
biases = [
np.array([0.0, 0.0, 0.0]), # 隠れ層1
np.array([0.0]) # 出力層
]
# モデルを定義
model = (layers, weights, biases)
# 仮の訓練データ(1件分)を準備
x = np.array([0.05, 0.1]) # x_1とx_2の2つの特徴量
変数weightsや変数biasesを多次元配列値ではなくリスト値にしているのは、行列の形状を気にする必要がないからです。NumPyの多次元配列では、各次元の要素数を一致させる必要があります。例えば行と列で構成される二次元配列で1行目が2列なら、2行目も2列にする必要があります。1行目が2列で、2行目が3列のようなチグハグ(ragged)な構造を作成することはできません。よって、各層をまとめたweightsやbiasesのような変数ではNumPyの多次元配列ではなくリストを使う必要があります。
また、リスト値の各要素はnp.array()というコードにより二次元配列や一次元配列となっています。NumPyの配列を格納している理由は、後述する順伝播における行列計算でそのまま使えるからです。
ちなみに基礎編や今回の応用編では、リスト2のように重みやバイアスの初期値(全て0)を手動で記述しています。これをNumPyで自動生成する方法を、ノートブックの方に「おまけ」として実装しておきました。
ステップ1. 順伝播の実装
1つの層における順伝播の処理
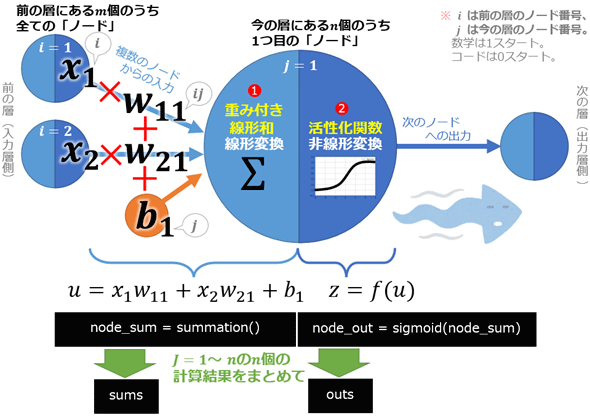
基礎編では、ニューラルネットの最小単位である「1つのノード」における順伝播の処理をコーディングしました。今回の応用編では、「1つの層」内にある「全ノード」における順伝播の処理をまとめてコーディングします。
# 取りあえず仮で、空の関数を定義して、コードが実行できるようにしておく
def summation(x, W, b):
" 重み付き線形和の関数。"
return np.array([0.0])
def sigmoid(x):
" シグモイド関数。"
return x
def identity(x):
" 恒等関数。"
return x
W = np.array([[0.0, 0.0]]) # 重み(仮の値)
b = np.array([0.0]) # バイアス(仮の値)
next_x = x # 訓練データをノードへの入力に使う
# ---ここまでは仮の実装。ここからが必要な実装---
# 1つの層内にある全ノードの処理(1): 重み付き線形和 u=Σx_i*w_i+b
sums = summation(next_x, W, b)
# 1つの層内にある全ノードの処理(2): 活性化関数 z=f(u)
is_hidden_layer = True
if is_hidden_layer:
# 隠れ層(シグモイド関数)
outs = sigmoid(sums)
else:
# 出力層(恒等関数)
outs = identity(sums)
基礎編では、1つのノード分の値をnode_sumとnode_outという変数に格納していました(図4)。今回の応用編では行列を使うことで、1つの層内にある全てのノード分の値を並列的にまとめて計算し、その結果をsumsとoutsという変数にまとめて格納しています。
重み付き線形和関数の数学的な定義は以下のようになり、本稿の数式ではその結果はuと表現しています(コードではsums)。
活性化関数の数学的な定義は以下のようになり、本稿の数式ではその結果はzと表現しています(コードではouts)。なお、関数fの内容は活性化関数の種類によって異なります。各活性化関数については後述します。
重み付き線形和
行列計算の内容を説明する前に、本稿での入力/重み/バイアスの行列内容について確認しておきましょう。今回の実装例では、1データごとに全ノード数分をまとめて計算することにします。そのため、前掲の図4の数式変数名を使って説明すると、以下のようになります。
※一般的な行列の定義は、以下のようになりますが、上のWはこれを転置した形になっている点に注意してください。前の層を基準に重みを並べると下のようになりますが(=前の層のノード1〜mのm行が縦に並ぶ)、今の層を基準に重みを並べると上のようになります(=今の層のノード1〜nのn行が縦に並ぶ)。
ベクトルであるx(入力)とb(バイアス)、行列であるW(重み)の3つの変数を使って図4のような重み付き線形和の計算式を成立させるには次のような計算式を組み立てればよいです。これが冒頭の図1に掲載した数式です。
このことから、実装コードはリスト4のようになります。
def summation(x, W, b):
"""
重み付き線形和の関数。
※1データ分×全ノード数分を処理する前提。
- 引数:
x: 入力データを一次元配列値(各要素はfloat値)で指定する。
W: 重みを二次元配列値(各要素はfloat値)で指定する。
b: バイアスを一次元配列値(各要素はfloat値)で指定する。
- 戻り値:
線形和の計算結果を一次元配列値(各要素はfloat値)で返す。
"""
linear_sums = np.dot(W, x) + b
# linear_sums = np.dot(x, W.T) + b # こう書いてもOK
return linear_sums
np.dot()関数は、行列積やベクトル同士の内積を行うためのものです。np.dot(W, x)というコードで、重み(W)と入力(x)の行列積を計算しています。np.dot()関数の代わりに@演算子やnp.matmul()関数を使っても同じ計算が行えます。
※同じ計算式が組み立てられるのであれば、線形代数の計算式は筆者の実装と同じである必要はありません。リスト4でコメントアウトした行にあるようにnp.dot(x, W.T) + bと書いた場合は、以下の計算式になり、結果は同じです。
リスト4(前掲の図1)を見ると、基礎編から比べて圧倒的にシンプルになった上に、全ノードをまとめて計算できています。行列計算の効率性はすごいですね。
同様の要領で、他に定義する関数も行列/ベクトル対応にしていきましょう。次に、重み付き線形和の偏導関数にもベクトル(x/b)や行列(W)を指定できるようにします(リスト5)。
def sum_der(x, W, b, with_respect_to='W'):
"""
重み付き線形和の関数の偏導関数。
※1データ分×全ノード数分を処理する前提。
- 引数:
x: 入力データを一次元配列値で指定する。
W: 重みを二次元配列値で指定する。
b: バイアスを一次元配列値で指定する。
with_respect_to: 何に関して偏微分するかを指定する。
'W'= 重み、'b'= バイアス、'x'= 入力。
- 戻り値:
with_respect_toが、
'W'の場合は二次元配列値(行ベクトル)で、
'b'の場合は一次元配列値(ベクトル)で、
'x'の場合は二次元配列値(行列)で、
線形和の偏微分の計算結果(偏微分係数)を返す。
"""
if with_respect_to == 'W':
return x.reshape(1, len(x)) # 線形和uを各重みw_ijで偏微分するとx_iになる(iはノード番号)
elif with_respect_to == 'b':
return np.ones(len(b)) # 線形和uをバイアスb_jで偏微分すると1になる
elif with_respect_to == 'x':
return W # 線形和uを各入力x_iで偏微分するとw_ijになる
x.reshape(1, len(x))というコードでは、ベクトルを表現する一次元配列のxを、行列における行ベクトルを表現する「1行m(=前の層にあるノードの数)列」の二次元配列に形状変換しています。必ずしもこの変換処理は必要ではありませんが、呼び出し元で続く行列計算の処理をしやすくするためです(もちろんここではなく、呼び出し元で処理してもOK)。
また、np.ones(len(b))というコードでは、1.0という値を「n(=今の層にあるノードの数)個」含む一次元配列を生成しています。
理論的にバイアス(b)は、前の層には関係がなく「今の層のノード数(j=1,2,…,nのn個)」だけ計算すればよいので、計算結果はn個の要素を持つベクトル(一次元配列)になります。
一方で、重み(W)や入力(x)は、「今の層のノード数(n個)」×「前の層のノード数(i=1,2,…,mのm個)」を計算するので、計算結果はn行m列の行列(二次元配列)になります。
しかし上のコードでは、重み(with_respect_to == 'W')がn行m列の行列ではなく、1行m列の行ベクトルになっている点に注意してください。これは実際にはj行m列を意図しており、今の層の何ノード目(j=1,2,…,n)であっても、計算結果が同じ値となるので、しかも行ベクトルの方が逆伝播のNumPyによる計算がしやすかったので、1行に要約しました。
活性化関数:シグモイド関数
シグモイド関数の数式定義は次の通りです。
上記の数式をコードにするとリスト6のようになります。他の数学関数も同じ形式で掲載するので、文章による説明は割愛します。
def sigmoid(x):
"""
シグモイド関数。
- 引数:
x: 入力データを一次元配列値で指定する。
- 戻り値:
シグモイド関数の計算結果を一次元配列値で返す。
"""
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_der(x):
"""
シグモイド関数の(偏)導関数。
- 引数:
x: 入力データを一次元配列値で指定する。
- 戻り値:
シグモイド関数の(偏)微分の計算結果(微分係数)を一次元配列値で返す。
"""
output = sigmoid(x)
return output * (1.0 - output)
活性化関数:恒等関数
def identity(x):
"""
恒等関数の関数。
- 引数:
x: 入力データを一次元配列値で指定する。
- 戻り値:
恒等関数の計算結果(そのまま)を一次元配列値で返す。
"""
return x
def identity_der(x):
"""
恒等関数の(偏)導関数。
- 引数:
x: 入力データを一次元配列値で指定する。
- 戻り値:
恒等関数の(偏)微分の計算結果(微分係数)を一次元配列値で返す。
"""
return np.ones(len(x))
順伝播の処理全体の実装
ニューラルネットには、層があり、その中に複数のノードが存在するという構造です。従って、
- 各層を1つずつ処理するforループと、
- 層の中の全ノードをまとめて処理する行列計算、の2段階構造が必要で、ここに行列計算を使った「順伝播の処理」
を記述すればよいわけです(リスト10)。
def forward_prop(layers, weights, biases, x, cache_mode=False):
"""
順伝播を行う関数。
- 引数:
(layers, weights, biases): モデルを指定する。
x: 入力データ(一次元配列値)を指定する。
cache_mode: 予測時はFalse、訓練時はTrueにする。これにより戻り値が変わる。
- 戻り値:
cache_modeがFalse時は予測値のみを返す。True時は、予測値だけでなく、
キャッシュに記録済みの線形和(Σ)値と、活性化関数の出力値も返す。
"""
cached_sums = [] # 記録した全ノードの線形和(Σ)の値
cached_outs = [] # 記録した全ノードの活性化関数の出力値
# まずは、入力層を順伝播する
cached_outs.append(x) # 何も処理せずに出力値を記録
next_x = x # 現在の層の出力(x)=次の層への入力(next_x)
# 次に、隠れ層や出力層を順伝播する
SKIP_INPUT_LAYER = 1
for layer_i, layer in enumerate(layers): # 各層を処理
if layer_i == 0:
continue # 入力層は上で処理済み
# 層ごとに全ノードまとめて処理を行う
sums = [] # 現在の層の全ノードの線形和
outs = [] # 現在の層の全ノードの(活性化関数の)出力
# 層ごとに全ノードの重みとバイアスを取得
W = weights[layer_i - SKIP_INPUT_LAYER]
b = biases[layer_i - SKIP_INPUT_LAYER]
# 1つの層内にある全ノードの処理(1): 重み付き線形和
sums = summation(next_x, W, b)
# 1つの層内にある全ノードの処理(2): 活性化関数
if layer_i < len(layers)-1: # -1は出力層以外の意味
# 隠れ層(シグモイド関数)
outs = sigmoid(sums)
else:
# 出力層(恒等関数)
outs = identity(sums)
# 各層内の全ノードの線形和と出力を記録
cached_sums.append(sums)
cached_outs.append(outs)
next_x = outs # 現在の層の出力(outs)=次の層への入力(next_x)
if cache_mode:
return (cached_outs[-1], cached_outs, cached_sums)
return cached_outs[-1]
# 訓練時の(1)順伝播の実行例
y_pred, cached_outs, cached_sums = forward_prop(*model, x, cache_mode=True)
# ※先ほど作成したモデルと訓練データを引数で受け取るよう改変した
print(f'cached_outs={cached_outs}')
print(f'cached_sums={cached_sums}')
# 出力例:
# cached_outs=[array([0.05, 0.1 ]), array([0.5, 0.5, 0.5]), array([0.])] # 入力層/隠れ層1/出力層
# cached_sums=[array([0., 0., 0.]), array([0.])] # 隠れ層1/出力層(※入力層はない)
基礎編ではfor node_i in range(layer):というコードでノードを1つずつ処理していましたが、これが行列計算により無くなっています。その他はほぼ同じコードです。
変数cached_outsや変数cached_sumsはリスト値となっていますが、その各要素は出力例のarray()という表記で分かる通り、NumPyの一次元配列となっています。NumPyの配列のまま格納している理由は、次の逆伝播の際の行列計算でそのまま使えるからです。
また、cached_outsやcached_sumsをリスト値にしているのは、リスト2で説明したのと同じ理由で、チグハグ(ragged)な構造を作成するには、NumPyの多次元配列ではなくリストを使う必要があるからです。
ちなみにノートブックの方では、コード中にprint()関数を仕込むことで(※全てコメントアウトしています)、途中の計算内容が順番にテキスト出力されるようにしてみました。リスト10では、以下のように出力されます。
■第1層(入力層)-全て(2個)の特徴量:
●入力データ: 何もしない=out([0.05 0.1 ])
■第2層-全ノード:
●重み付き線形和: W([[0. 0.] [0. 0.] [0. 0.]])・x([0.05 0.1 ])+b([0. 0. 0.])=sum([0. 0. 0.])
●活性化関数(隠れ層はシグモイド関数): sigmoid([0. 0. 0.])=out([0.5 0.5 0.5])
■第3層-全ノード:
●重み付き線形和: W([[0. 0. 0.]])・x([0.5 0.5 0.5])+b([0.])=sum([0.])
●活性化関数(出力層は恒等関数): identity([0.])=out([0.])
cached_outs=[array([0.05, 0.1 ]), array([0.5, 0.5, 0.5]), array([0.])]
cached_sums=[array([0., 0., 0.]), array([0.])]
数値が0.0ばかりなので参考になりませんね・・・・・・。後述のリスト11を参考に重みやバイアスなどを変えてみて、本当に計算通りになるかのチェックなどをしてみてもよいでしょう(※ノートブックの方には別の計算パターンのコードも入れておきました)。
順伝播による予測の実行例
何カ所かnp.array()関数を呼び出している以外は、基礎編と全く同じコードです。
# 異なるDNNアーキテクチャーを定義してみる
layers2 = [
2, # 入力層の入力(特徴量)の数
3, # 隠れ層1のノード(ニューロン)の数
2, # 隠れ層2のノード(ニューロン)の数
1] # 出力層のノードの数
# 重みとバイアスの初期値
weights2 = [
np.array([[-0.2, 0.4], [-0.4, -0.5], [-0.4, -0.5]]), # 入力層→隠れ層1
np.array([[-0.2, 0.4, 0.9], [-0.4, -0.5, -0.2]]), # 隠れ層1→隠れ層2
np.array([[-0.5, 1.0]]) # 隠れ層2→出力層
]
biases2 = [
np.array([0.1, -0.1, 0.1]), # 隠れ層1
np.array([0.2, -0.2]), # 隠れ層2
np.array([0.3]) # 出力層
]
# モデルを定義
model2 = (layers2, weights2, biases2)
# 仮の訓練データ(1件分)を準備
x2 = np.array([2.3, 1.5]) # x_1とx_2の2つの特徴量
# 予測時の(1)順伝播の実行例
y_pred = forward_prop(*model2, x2)
print(y_pred) # [0.38288404]
今後のステップの準備:関数への仮引数の追加
基礎編と全く同じコードです。
def back_prop(layers, weights, biases, y_true, cached_outs, cached_sums):
" 逆伝播を行う関数。"
return None, None
def update_params(layers, weights, biases, grads_w, grads_b, lr=0.1):
" パラメーター(重みとバイアス)を更新する関数。"
return None, None
次のページでは逆伝播の処理をNumPy/線形代数で実装します。今回の山場になります。
Copyright© Digital Advantage Corp. All Rights Reserved.