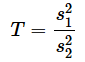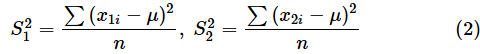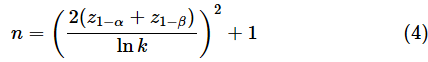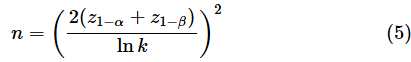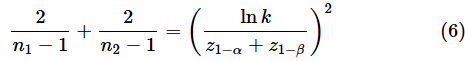【Excelで学ぶデータ分析】寿司職人の腕はロボットよりも正確かを調べたい（F検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第5回。今回は、正規分布する2つの母集団の分散が等しいかどうかを調べる方法について解説します。

» 2025年10月27日 05時00分公開

連載：

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第5回です。前回は、正規分布する母集団の分散がある値よりも大きいかどうかを調べるために、分散の検定を行う方法を解説しました。今回は正規分布する2つの母集団について、分散の比の検定（F検定）を行います。具体的には、一方の分散が小さいかどうかを調べたい場面を想定した事例を取り上げます。

母分散の比の検定についての基本的な考え方

　前回のテーマは母分散の検定でしたが、今回のテーマは母分散の比の検定です。帰無仮説と、利用する分布の観点から、それらの違いについて確認しておきましょう。


検定の種類	帰無仮説	利用する分布
母分散の検定（前回）	1つの母集団の分散がある値と等しい	カイ二乗分布
母分散の比の検定（今回）	2つの母集団の分散は等しい	F分布

表1　母分散の検定と母分散の比の検定
母分散の検定は1つの群について、母分散がある値と等しいかどうかを検定する。今回のテーマである「母分散の比の検定」では2つの群について、それらの母分散が等しいかどうかを検定する。後者は母分散の「差」の検定とも言われることがあるが、実際には「比」を使う。

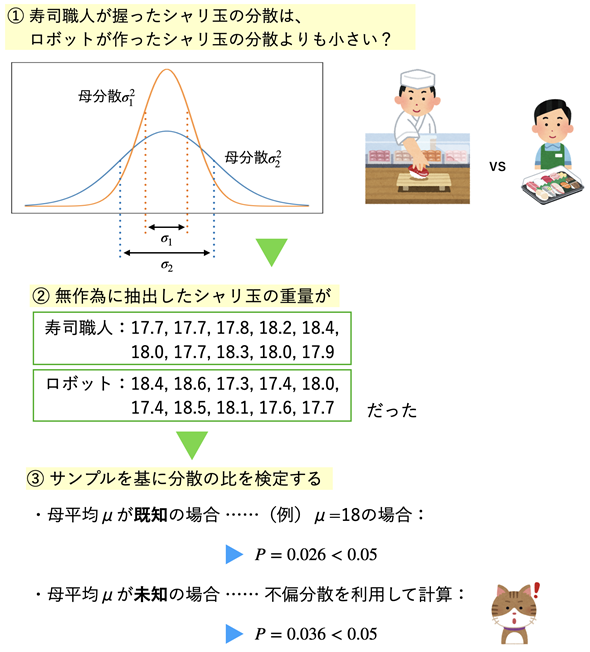
　事例を見た後、帰無仮説と対立仮説を立てることにします。図1は、ベテラン寿司職人が握ったシャリ玉（お寿司のごはんの部分）とロボットによって作られたものを無作為に10個ずつ取り出し、重さを量った例です（架空のデータです）。ベテラン寿司職人になると機械で握る以上の正確さを持っていそうですね。ということは、分散はロボットよりも小さいものと予想されます。

図1　シャリ玉のバラツキは、寿司職人の方が小さい？
ここでは、寿司職人のシャリ玉の方が、分散が小さいことを確かめたい。母平均が既知の場合と未知の場合で計算方法が異なる。

　そこで、母分散の比の検定を行ってみたいと思います。まず、母分散の比の検定を行うためには、大前提として母集団が正規分布していることが必要であることに注意してください（正規分布が仮定できない場合については後述します）。

　寿司職人が握ったシャリ玉の分散をσ₁²、ロボットによって作られたシャリ玉の分散をσ₂²として、帰無仮説H₀と対立仮説H₁を立ててみましょう。

H₀：母分散は等しい（σ₁²＝σ₂²）
H₁：寿司職人の母分散の方が小さい（σ₁² < σ₂²）

　この場合は、対立仮説がσ₁² < σ₂²なので、片側検定となります。母分散の比の検定については、母平均が既知の場合と未知の場合とで計算方法が異なりますが、Excelでは母平均が未知の場合の方が簡単にできるので、そちらから先に見ていきます。

母分散の比の検定を行ってみよう～母平均が未知の場合

　母平均が未知の場合、F.TEST関数を使えば簡単にP値が求められます。ただし、F.TEST関数は両側確率を返すので、片側検定の場合は得られた値を2で割る必要があります。

　こちらからダウンロードしたExcelファイルを開いて試してみてください。［母分散の比の検定 (母平均が未知)］ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

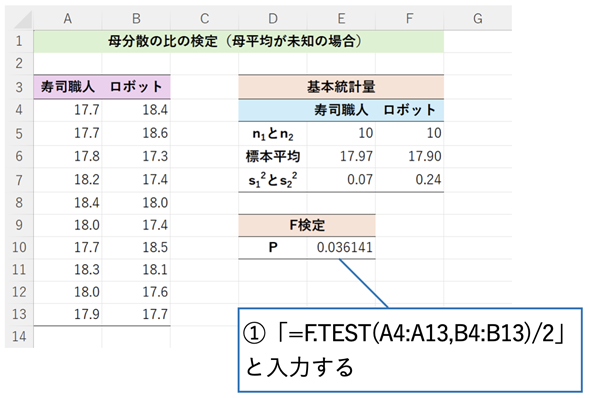図2　母分散の比の検定（母平均が未知の場合）
図中のs₁²とs₂²はそれぞれの不偏分散。寿司職人の分散が小さいように見える。そこで、F.TEST関数を使って母分散の比の検定を行う。母平均が未知の場合はF.TEST関数で両側確率が求められる。ここでは片側確率を求めたいので、F.TEST関数の結果を2で割っている。

　結果は、P＝0.036<0.05なので5％有意となり、対立仮説の「寿司職人の母分散の方がロボットの母分散よりも小さい」を採用します。寿司職人の方が安定して平均に近い重さのシャリ玉を握っているといえそうです。といっても、あくまで架空のデータなので、実際のところはどうなのか分かりません（別に寿司ロボットをディスっているわけではありません、念のため）。

検定統計量TとF分布の累積分布関数によって検定を行うには

　図2で見たように、母平均が未知の場合、詳細な計算の方法を知らなくても、F.TEST関数を利用するだけで母分散の比の検定（以下、F検定と呼びます）ができてしまいます。しかし、検定統計量Tを求め、F分布を基にP値を求める方法も知っておきたいですね。

　F検定では、検定統計量Tは、

で求められます。s₁²とs₂²はそれぞれの不偏分散です（VAR.S関数で求められる値ですね）。P値は、検定統計量Tに対するF分布の累積分布関数の値となります。F分布の自由度はそれぞれのサンプルサイズから1を引いた値、つまり、n₁－1とn₂－1です。

　対立仮説H₁がσ₁² < σ₂²の場合はF.DIST関数を使って左側確率を求め、対立仮説H₁がσ₁² > σ₂²の場合はF.DIST.RT関数を使って右側確率を求めます。対立仮説H₁がσ₁² ≠ σ₂²の場合（両側検定の場合）はF.DIST関数で求めた左側確率と、1－左側確率の小さい方を2倍します。

　F分布の累積分布関数を表す式（定義）はかなり難しいので、ここでは省略しますが、こちらに掲載してあるので、興味のある方は参照してみてください。Excelを利用するなら、定義通りに計算しなくてもF.DIST関数で左側確率が、F.DIST.RT関数で右側確率が求められます。サンプルファイルの［母分散の比の検定 (母平均が未知・作成例)］にはVAR.S関数とF.DIST関数を使って計算した例も含めてあります。

　続いて、母分散の比の検定（母平均が既知の場合）を行ってみましょう。

母分散の比の検定を行ってみよう～母平均が既知の場合

　母平均が既知の場合には、F.TEST関数が使えません。そのため、以下の式で検定統計量Tを求め、F.DIST関数またはF.DIST.RT関数を使ってP値を求めます。

　ただし、

とします。S₁²やS₂²はVAR.P関数で求められる標本分散の値とは異なることに注意が必要です。各データから母平均を引き、それを2乗した値の総合計をデータの個数で割る、ということです。

　（1）式で求めたTの値を基に、自由度n₁, n₂のF分布の左側確率をF.DIST関数で求めてみましょう。［母分散の比の検定 (母平均が既知)］ワークシートを表示して、図3のように操作してみてください。母平均が18であると分かっている場合の計算例です。

図3　母分散の検定（母平均が既知の場合）
セルE6とF6の値はAVERAGE関数を使って求めた標本平均ではなく、既に分かっている母平均の値が入力されていることに注意。（2）式のS₁²の値は、セルE7に「=SUM((A4:A13-E6)^2)/D5」と入力して求める（※Excel 2019以前のバージョンは2025年10月14日に延長サポートが終了したため、今回から対象外とする）。S₂²の値はセルE7をセルF7にコピーすれば求められる。これらの値を基に、セルE10で（1）式により検定統計量Tを求める。セルE11のF.DIST関数に検定統計量Tとn₁,n₂の値、累積分布関数の値を求めるためのTRUEを指定すればP値が求められる。

　なお、Googleスプレッドシートでは、セルE7には「=ARRAYFORMULA(SUM((A4:A13-E6)^2)/E5)」と入力します。

　結果は、P＝0.026<0.05なので5％有意となり、対立仮説の「寿司職人の母分散の方がロボットの母分散よりも小さい」を採用します。

　なお、この例とは異なる対立仮説での計算方法については、母平均が未知の場合と同じ考え方です（上の、アイ博士の注釈を参照）。

　母平均が既知である場合はあまり考えにくいかもしれません。実は、寿司ロボットでは、シャリの重量を何種類か指定できるようになっています。例えば、旧機種で18gと設定して握った場合と、新機種で18gと設定して握った場合の分散の比を検定したい場合には、母平均が既知であるものと仮定できます。

コラム　F検定とt検定の利用における落とし穴

　この連載の第3回で、母平均の差の検定（t検定）を取り上げました。t検定では、母分散が等しいと仮定できる場合と、等しいと仮定できない場合とで、検定の方法が異なります。今回のF検定を利用すれば、母分散が等しいかどうかを検定できるので、F検定を行って、母分散が等しいということを確かめてから、t検定を適用したい、と考える人がいるかもしれません。

　しかし、連載の第1回でも解説したように、帰無仮説（母分散は等しい）が棄却できなかったからといって、帰無仮説が正しいというわけではありません。そのような、確実さに欠ける前提の下でt検定を行うと、検定の精度が低下してしまいます。

　従って、母分散が等しいかどうかが不明な場合には、最初から、母分散が等しいと仮定できない場合のt検定（ウェルチの検定）を行うべきです（第3回で解説済み）。

母集団が正規分布であると仮定できない場合は？～ルビーン検定とブラウン・フォーサイス検定

　F検定は母集団が正規分布に従っていることを前提としています。正規分布であることが仮定できない場合に、分散の比を検定するにはルビーン（Levene）検定やブラウン・フォーサイス（Brown-Forsythe）検定が便利です。

　ルビーン検定やブラウン・フォーサイス検定は、分散という母数に関する検定ではなく、平均や中央値からの差の絶対値を基にした検定です（計算方法は後述します）。厳密な意味での分散の比の検定ではありませんが、ばらつきに関する検定なので、一般に分散の比の検定と呼ばれます。

　ルビーン検定やブラウン・フォーサイス検定では3群以上の比較もできます。従って「全ての群の母分散が等しい」という帰無仮説に対して、「母分散が異なる群がある」という対立仮説を立てます。2群を比較してどちらかの分散が大きい、といった対立仮説が立てられないことに注意が必要です。

　ルビーン検定とブラウン・フォーサイス検定の手順は同じで、前者が標本平均を利用するのに対して、後者が中央値を利用するという違いがあるだけです。

　ここでは、Pythonのプログラムを使ってブラウン・フォーサイズ検定を行った例を紹介します。サンプルプログラムはこちらを参照してください。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］+［Enter］キーを押せば、コードが実行できます。

　以下に示すのがブラウン・フォーサイス検定の例です。scipy.statsモジュールのlevene関数を呼び出すだけなので、簡単ですね。検定統計量とP値が一度に求められます。

from scipy.stats import levene
import numpy as np

# サンプル
x = np.array([17.7, 17.7, 17.8, 18.2, 18.4, 18.0, 17.7, 18.3, 18.0, 17.9])
y = np.array([18.4, 18.6, 17.3, 17.4, 18.0, 17.4, 18.5, 18.1, 17.6, 17.7])

T, p = levene(x, y, center='median') # ブラウン・フォーサイス検定
print(f'T={T:.3f}, pvalue={p:.3f}') # 検定統計量とP値を表示

# 実行例
# T=7.025, pvalue=0.016

リスト1　ブラウン・フォーサイス検定のコード例
scipy.statsモジュールのlevene関数では、各群の値を指定するだけで分散の比の検定ができる。center='mean'を指定するとルビーン検定となる（省略時は、中央値を表す'median'が指定されたものと見なされるので、上のコードではcenter=を指定しなくても同じ結果になる）。

　話を簡単にするために、2群を比較するものとして、ブラウン・フォーサイス検定での計算の手順を紹介します。

　計算そのものは単純ですが、やや面倒かもしません。この手順に従ってExcelで計算した例を参考としてサンプルファイルの［ブラウン・フォーサイス検定］ワークシートに含めてあります。

母分散の比の検定での適切なサンプルサイズは？

　最後に、適切なサンプルサイズの求め方を見ておきます。ここでは、理屈抜きに、標準正規分布を使って近似値を求めるための式を示しておきます。有意水準をα、検出力を1－βとし、効果量を分散の比k＝σ₁²/σ₂²としたとき、母平均が未知の場合は以下の式を使います。

　母分散が既知の場合は以下の式を使います。

　z_1－αは標準正規分布の1－α点の値です（両側検定の場合はz_1－α/2とします）。また、lnは自然対数です。

　具体例で計算してみましょう。α＝0.05、1－β＝0.8とし、効果量をr＝0.3とします。z_1－α＝1.645, z_1－β＝0.842, ln k＝－1.204なので、母分散が未知の場合、（4）式に当てはめて、

となります。標準正規分布で近似した計算なので、余裕を見て＋1～＋2としておくのがいいでしょう。参考として、サンプルファイルの［サンプルサイズ (母平均未知)］ワークシートにこの計算例を含めてあります。また、［サンプルサイズ (母平均既知)］には（5）式での計算例を含めてあります。

　上の例では、2群のサンプルサイズが同じ（n）であるものとしましたが、サンプルサイズが異なることが想定されることもあると思います。そのような場合は、以下の式を使います（母平均が未知の場合の例です。母平均が既知の場合は－1は不要です）。

　とはいえ、1つの式にn₁,n₂という2つの未知数があるので、これだけでは答えが求められません。そのような場合は、サンプルサイズの比をrとして、n₂＝rn₁とし、（6）式を解きます。が、かなり面倒そうですね（二次方程式になります）。そこで、Excelのゴールシークを利用してみましょう。［サンプルサイズ (ゴールシーク)］ワークシートで、図4に示した式は既に入力されているので、図の後に示した手順でゴールシークを適用します。

図4　ゴールシークを利用してn₁,n₂を求めるための準備
ここでは、r＝2としてn₁とn₂を求める。セルB4が（6）式の左辺の値なので、これを（6）式の右辺の値（セルB8の値）に近づくようにセルB4の値を変えていけばよい。ゴールシークの操作方法は、以下に箇条書きで示す。

　ゴールシークの手順は以下の通りです。Googleスプレッドシートの場合は手順をサンプルファイルの中に記してあります。

［データ］タブを開き［What-If分析］-［ゴールシーク］を選択する
［数値入力セル］ボックスをクリックして、セルB8をクリックする
［目標値］ボックスに0.234と入力する（右辺の値）
［変化させるセル］ボックスをクリックして、セルB4をクリックする
［OK］ボタンをクリックする

　r＝2の場合、n₁≈ 14,n₂≈28という結果が得られます（余裕を見て、n₁＝15,n₂＝30としておくといいでしょう。なお、n1＝n2の場合はセルB3に1と入力しておきます。

　実用的には、上の近似計算で問題はありませんが、必要なサンプルサイズをより正確に見積もるには、F分布を利用し、検出力が1－β以上になるnの値を求めます。Excelでもできますが、繰り返し処理が必要になるので、Pythonでプログラムを作成した方が簡潔に表せます。ブラウン・フォーサイス検定の例と同じファイルにその例を含めてあります。2つ目のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。n1=15, n2=30という結果が表示されます。

　今回は、母分散の比の検定方法を解説しました。今回までで、比較的よく使う母平均の検定、母平均の差の検定、母分散の検定、母分散の比の検定を一通り見たことになります。目的によって利用する確率分布は異なりますが、基本的な考え方や手順はほとんど同じでしたね。

　適切なサンプルサイズの求め方も併せて解説しましたが、計算がかなり面倒でした。そこで、次回（番外編）は、ちょっとした気分転換として、サンプルサイズや効果量などを簡単に求めるためのツール（G*Power）を紹介することにします。次回もお楽しみに！