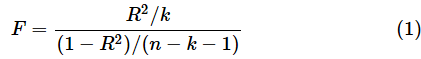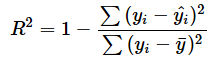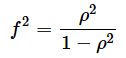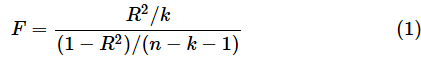【Excelで学ぶデータ分析】年式、走行距離、排気量から中古車の価格はうまく求められるか？（重回帰式の当てはまりの良さを検定）：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第9回。今回は、重回帰分析における回帰式の当てはまりの良さを検定する方法について解説します。

» 2025年12月22日 05時00分公開

連載：

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第9回です。前回は、中古車の排気量と価格の例で相関係数の検定を紹介しました。今回も中古車の例を利用して重回帰分析を行い、回帰式の当てはまりの良さを検定します。

回帰式の当てはまりの良さとは、その検定とは？

　回帰分析とは、説明変数を基に、目的変数の値を得るための回帰式を求めることでした。説明変数が1つの場合は「単回帰分析」と呼び、複数の場合には「重回帰分析」と呼ぶ、ということです。回帰分析の方法については、『やさしいデータ分析』の第14回で単回帰について、第15回で重回帰についての考え方や計算方法を詳しく解説しています（今回の事例と値は異なりますが、やはり中古車の例を使っています）。

　回帰式が一次式で表される線形回帰を例として、ごく簡単におさらいしておきましょう。回帰分析とは、説明変数をx₁,x₂, ..., x_nとし、目的変数をyとすると、

のような回帰式の定数項と係数を求めることでした。a₀が定数項で、a₁以降が各説明変数の係数です。中古車の価格の例であれば、

という回帰式が立てられます。定数項（a₀）と係数（a₁,a₂,a₃）が求められれば、年式、走行、排気量（これらが説明変数）を基に本体価格（目的変数）の値が予測できます。

　定数項や係数を求めるための計算方法はかなり複雑ですが、ExcelではLINEST関数を使えば簡単に求められます。図1にはLINEST関数で求めた回帰式を示してありますが、今回の目標はその回帰式がデータに良く当てはまっているかどうかを検定する、ということです。具体的には、年式、走行、排気量から中古車の本体価格がうまく求められるかどうかを知りたいわけです。図には実在の車名を記載してありますが、データは架空のものです。

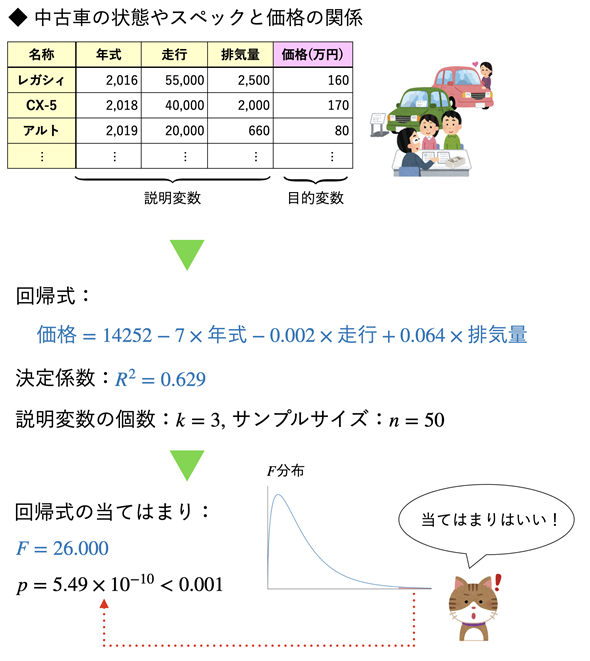図1　中古車の年式、走行、排気量から価格がうまく求められるか？
回帰式の定数項や係数、決定係数R²、検定統計量FはLINEST関数を使えば簡単に求められる（図のブルーの文字で書かれた部分）。決定係数R²が回帰式の当てはまりの良さを表す。検定ではR²の値を基に検定統計量Fを求め、続いて、F分布の右側確率を求める。

　例によって、帰無仮説と対立仮説の確認から始めます。

帰無仮説（H₀）：回帰式の当てはまりは良くない
対立仮説（H₁）：回帰式の当てはまりは良い

　「回帰式の当てはまり」というのはずいぶんとあいまいな言い方ですが、回帰式の当てはまりの良さは、決定係数R²などで表されます。そのR²に関する検定となるわけです（実質的にR²＝0であるかどうかの検定となります）。回帰式の係数や定数項に加え、決定係数R²もLINEST関数で簡単に求められます。また、検定統計量Fも併せて求められます。

回帰式の当てはまりの良さを検定してみよう

　重回帰分析の当てはまりの良さを検定するためには、まず、検定統計量Fを以下の式で求めます。nはサンプルサイズ、kは説明変数の個数です。

　上でも触れたように、実際には（1）式で計算しなくても、LINEST関数によって検定統計量Fの値が求められます。Fの値が求められたら、F分布の右側確率を求めます。R²は必ず正になるので、対立仮説はR²≠0ではなく、R²>0と考えられる（片側検定になる）からです。F分布の右側確率はF.DIST.RT関数で求められます。自由度は(k,n－k－1)となります。

　では、こちらからダウンロードしたExcelファイルを開いて試してみてください。［重回帰の検定］ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

図2　回帰式の当てはまりの良さを検定する
表を見やすくするために、上にサンプル（D列～I列）を、下に重回帰分析の結果と検定結果（K列～O列）を分けて示してある（サンプルファイルではこれらの表は横に並んでいる）。セルL4にLINEST関数を入力し、係数や定数項、補正項を求めている。R²はセルL6に表示されており、F値はセルL7に表示されている。セルM7の値はn－k－1の値。セルL10にF.DIST.RT関数を入力し、F値と自由度(k, n－k－1)を指定しP値を求めている。

　セルL4に入力したLINEST関数には、目的変数の範囲、説明変数の範囲、定数項を求めるかどうか（求める場合はTRUE）、補正項を求めるかどうか（求める場合はTRUE）を順に指定します。

　LINEST関数によって求められた回帰式の係数は、元の列とは逆順に表示されることに注意が必要です。元の列が「年式」「走行」「排気量」の順であれば、LINEST関数で求めた係数は、「排気量」「走行」「年式」の順に並び、その後に定数項の値が表示されます（セルL4～O4）。

　補正項を求めると図のセルL4～O8までの値が求められます。補正項にはR²やF値などの値が表示されます。#N/Aと表示されているのは、そのセルで求められる値が特にないためです。結果を見ると、R²が0.629、F値が26.000となっていることが分かりますね。

　後は、セルL10のようにF.DIST.RT関数を入力してP値を求めるだけです。F.DIST.RT関数にはF値と自由度(k, n－k－1)を指定します。結果は、P＝5.49E－10<0.001というかなり小さな値になりました（E－10は10^－10＝1/10¹⁰を表します）。この結果から、0.1％有意で帰無仮説H₀を棄却し、対立仮説H₁を採用します。従って、「回帰式の当てはまりは良い」と言えます。

　決定係数R²を求めるための式は以下の通りです。

　サンプルファイルにも、上記の式に従ってR²を求めた例を［決定係数］ワークシートに掲載しています（ワークシート内に簡単な解説を含めてあります）。

回帰式の当てはまりの良さを検定する際の適切なサンプルサイズは？

　回帰式の当てはまりの良さを検定するに当たって、適切なサンプルサイズnを求める方法としては経験則が幾つかありますが（後述）、うまく適用できない場合も多いので、非心F分布を利用したプログラムやG*Powerを利用するのが簡単かつ、適切です。Pythonのプログラムはこちらに作成してあるので、興味のある方はご参照ください。

　最初のコードセルに入力されたプログラムは、説明変数の個数をk＝3とし、決定係数をρ²＝0.4と想定して、α＝0.01, 1－β＝0.95で計算した場合の例となっています（決定係数については、サンプルから得られたR²と区別するためにρ²と表記しています）。コードセルをクリックし、［Shift］＋［Enter］キーを押してプログラムを実行するとn=40という結果が表示されます。

　なお、想定される効果量（Cohen's f²）は、ρ²を基に以下の式で求めます。

　例えば、ρ²＝0.4であれば、f²＝0.4/(1－0.4)＝0.667となります。効果量の目安は以下の通りです。

小：f²＝0.02
中：f²＝0.15
大：f²＝0.35

　サンプルプログラムは効果量がかなり大きい場合の例となっています。ρ²を小さくする（＝効果量を小さくする＝小さな差も検出できるようにする）と、必要なサンプルサイズは大きくなります。値を変えて試してみてください。

　経験則としては、以下の式で表されるGreenの経験則がよく知られています。kは説明変数の個数です。

　ただし、この経験則は想定される効果量が中程度で、k<7の場合にのみ、α＝0.05, 1－β＝0.8に対する値が求められるということに注意が必要です。事前に効果量などに関する知見がなく、見積りができない場合にのみ、便宜的に使える方法だと考えておいていただくといいでしょう。

　プログラミングが苦手な方は、第6回で紹介したG*Powerを使うのが簡単です。図3のような画面での操作になります。手順は画面の後に箇条書きで記しておきます。

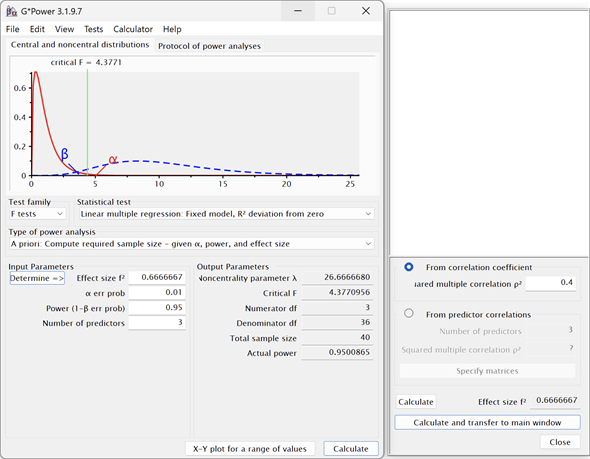図3　G*Powerで回帰式の当てはまりの良さを検定する際のサンプルサイズを求める
効果量f²＝0.667、有意水準α＝0.01、検出力1－β＝0.95、説明変数の個数k＝3の場合の例。回帰式の当てはまりの良さを検定するために必要なサンプルサイズは40となる。

　G*Powerでの操作手順は以下の通りです。検定の方法などを以下のように選択します。

［Test family］のリストから「F tests」を選択する
［Statistical test］のリストから「Linear multiple regression: Fixed model, R² deviation from zero」を選択する
［Type of power analysis］のリストから「Compute required sample size - given α, power, and effect size」を選択する

　メニューバーから［Tests］－［Linear multiple regression: Fixed model, R² deviation from zero］を選択しても同じ設定になります。

　上記の指定ができたら、以下のように操作します。

［Determine =>］ボタンをクリックする
右側に表示されたパネルで［From correlation coefficient］オプションを選択する
［Squared multiple correlation ρ²］ボックスに0.4と入力する
［Calculate and transfer to main window］ボタンをクリックする（左側のウインドウの［Effect size f²］ボックスに、効果量として0.6666667という値が表示される）
［α err prob］ボックスに0.01と入力する
［Power (1-β err prob)］ボックスに0.95と入力する
［Calculate］ボタンをクリックする

　以上の操作を行うと［Total sample size］として40という値が表示されます。

　ところで、回帰式の当てはまりの良さを検定する場合も、相関係数の検定などと同様、サンプルサイズが大きくなるとP値が小さくなるという「落とし穴」があります。（1）式を再掲します。

　この式を見ると、nが大きくなると、分母の(1－R²)/(n－k－1)が小さくなることが分かります。とすると、F値は大きくなります。F値が大きくなるとF分布の右側確率（P値）は小さくなりますね。サンプルファイルの［サンプルサイズとP値］ワークシートにシミュレーションを行った結果を含めてあります。例えば、k＝3の場合、R²＝0.005という小さな値であっても、nが1570以上になるとP<0.05となってしまいます（正確にはn＝1563でP<0.05となります）。

　ここでは、検定の方法を理解することを優先したので、一般的になじみのある中古車の事例を使いましたが、サンプルサイズが数千以上になるような調査であれば、検定によって回帰式の当てはまりが良いかどうかを判断することにはあまり意味がありません。中古車や不動産物件などの大量データや、全国を対象とした生活習慣や学力調査などでは、検定を行ってその結果に一喜一憂するよりも、R²の値や事後の効果量、さらには係数の意味などについての考察が重要になってくるというわけです（それは、サンプルサイズが限られる医学や生物学、心理学の実験などで検定を行う場合でも同じことですが）。

　今回は、重回帰分析における回帰式の当てはまりの良さを検定する方法について、その考え方やサンプルサイズの見積りなどを解説しました。上でも少し触れましたが、重回帰分析においては、回帰式の当てはまりの良さだけでなく、係数の有効性も気になるところです。

　そこで、次回は係数の有効性についての検定方法を取り上げて解説します。次回もお楽しみに！

「やさしい推測統計（仮説検定編）」