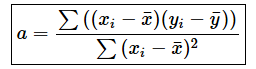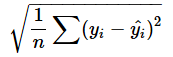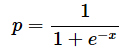［データ分析］単回帰分析による予測（線形回帰、指数回帰） 〜 排気量から中古車の価格を予測しよう：やさしいデータ分析

データ分析の初歩からステップアップしながら学んでいく連載の第14回。既知のデータから未知の値を「予測」する回帰分析の式の可視化や、求め方、実際の予測を、Excelを使って手を動かしながら学んでいきましょう。直線の式だけでなく指数関数の式での予測や時系列分析についても触れます。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしいデータ分析』

　この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
　データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト（ExcelやGoogleスプレッドシート）を利用した作成例を紹介します。
　必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入（またもや金欠）。

　これまでは、集団の性質や変数同士の関係など、何らかの「特徴」を見極める方法を紹介してきました。例えば前回は、相関係数を求めて変数同士の関係を数値で表す方法を紹介しました。

　今回からは、既に得られたデータから、未知の値を「予測」することに焦点を当て、回帰分析に取り組みます。回帰分析の方法を紹介するだけでなく、予測の精度を上げるための工夫についても見ていきます。今回取り上げるのは回帰分析による予測の第一歩、単回帰分析です。Excelを使って手を動かしながら単回帰分析にチャレンジしてみましょう。

　単回帰分析とは、ある変数xの値からもう一方の変数yの値を予測するための式（回帰式）を求めたり、回帰式を基に予測したりすることです。例えば、図1のように排気量から中古車の本体価格を予測するといった例がそれに当たります。なお、図1のデータでは実際のメーカーや車種の名称が使われていますが、本体価格などの値は架空のものです。

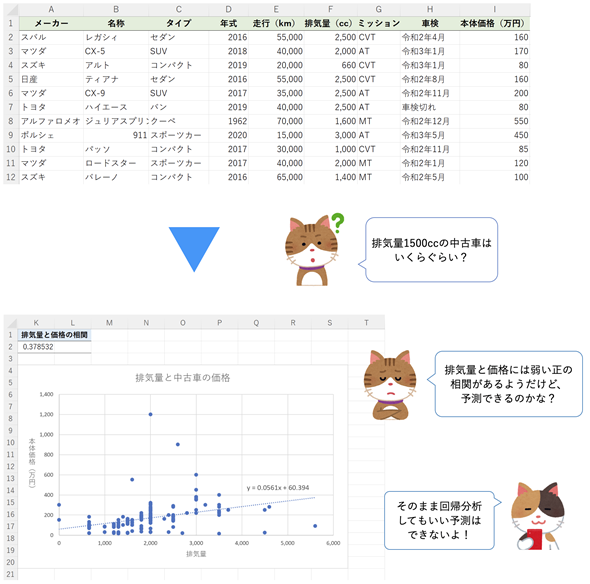図1　中古車のデータ（ここでは排気量と本体価格に注目する）
中古車の価格はさまざまな要因で決められるが、ここでは排気量と本体価格のみに注目する。取りあえず散布図を描いて回帰式を可視化したものがこの例。実際には、予測の精度を上げるために、相関係数や散布図から得た手掛かりを基に準備（前処理）を行う必要がある。が、最初の一歩として、このまま回帰分析を行ってみよう。

　図1に表示されている散布図には、各データの近くを通る点線の直線が引かれていますね。その直線を表す式が回帰式です。回帰式を利用すれば排気量から本体価格が予測できるというわけです。

　回帰分析では、xに当たる変数を説明変数と呼び、yに当たる変数を目的変数と呼びます。中古車データの例であれば、排気量が説明変数x、本体価格が目的変数yとなります。

　本来は、図1のように相関係数を求めたり、散布図を描いたりしてデータの特徴を見極め、より良い予測のための前処理を行ってから回帰分析に取り組むのが筋です。しかし、そもそも回帰分析の方法を知らないと実感が湧かないでしょうから、まずは、前処理なしで回帰分析を行ってみます。Excelではグラフを作成したり、幾つかの関数を使ったりするだけで簡単に回帰分析や予測ができてしまうので、先に結果を出してみようというわけです。その後、図1の下に記されている問題意識に対処して、前処理を行い、予測の精度を向上させる方法を見ていくことにします。

　ここでは、話を単純化するために回帰式を「直線を表す式」としていますが、実は直線でなくても構いません。例えば、xの値が大きくなるとyの値が急激に大きくなるような場合、指数関数を回帰式とした方が当てはまりがよくなります（指数回帰）。なお、最後のコラムでは、値の増減に波があるデータについて予測するための時系列分析についても簡単に触れます。

　回帰式が直線などの一次関数の場合を線形回帰と呼び、回帰式が指数関数の場合を指数回帰と呼びます。また、説明変数が1つだけ（xのみ）の回帰分析を単回帰と呼び、説明変数が複数（x₁, x₂, ...）の場合は重回帰分析と呼びます。今回は特に必要がなければ、線形回帰の単回帰分析を「回帰分析」と呼ぶことにします。

---

　この記事は、データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第14回です。第13回から第15回までは「関係」に注目し、相関係数や回帰分析などについて見ていきます。前回（第13回）は、相関係数の意味や求め方に加え、順序尺度や名義尺度での変数同士の関係を見極める方法を紹介しました。今回は、説明変数から目的変数の値を予測するために、単回帰分析の考え方や取り扱いを見ていきます。次回（第15回）は、複数の説明変数を利用する重回帰分析や、回帰式が二次以上の式になる多項式回帰に取り組む予定です。連載のトップページから全体の目次が参照できます。また、次回を見逃さないために記事冒頭のボタンからぜひメール通知にご登録ください。

この記事で学べること

　今回は以下のようなポイントについて、分析の方法や目の付けどころを見ていきます。

• 回帰式の可視化 …… 散布図に回帰式を表す直線（または曲線）を表示する
• 回帰式の求め方 …… 単回帰分析の回帰式（係数と定数項）を求める
• 回帰式による予測 …… 回帰式に値を代入して予測する
• 回帰分析のための準備 …… 予測の精度を上げるための前処理を行う
• 指数回帰についても理解する …… 直線的でない関係でも回帰分析を行う

　では、散布図を作成して回帰式を可視化した後、基本の基本である回帰式の係数と定数項の求め方に進みます。サンプルファイルの利用についての説明の後、本編に進みましょう。

サンプルファイルの利用について

　本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントで使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントで使える無料のGoogleスプレッドシート（Google Sheets）をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、ファイルを共有して参照できるようにします。リンクを開き、メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

視覚的に回帰分析を理解しよう 〜 回帰式の可視化

　既に述べたように、回帰分析とは、各データの最も近くを通る回帰式を求めたり、その式を基に予測したりすることです。ここでは、線形回帰に取り組むので、回帰式は直線を表す一次式になります。単回帰なので説明変数xは1つです。つまり、中学校で学んだ、

が回帰式となります。式の中のそれぞれの文字の意味は以下の通りです。

• 変数：
  • y …… 目的変数（ここでは、中古車の本体価格）： この値を予測したい
  • x …… 説明変数（ここでは、排気量）： 予測にはこの値を使う
• 定数：
  • a …… 係数： 直線の傾き
  • b …… 定数項： x＝0のときのyの値。切片とも呼ばれる

　回帰式y＝ax＋bを求めるということは、既に分かっている幾つかのyとxの値を基に、それらの値の近くを通る直線（つまり係数aと定数項bの値）を求めるということです。「近くを通る」というのはずいぶんとあいまいな言い方ですが、正確な意味については後述するので、今のところはあまり気にせずに進めましょう。

　まず、図1に示したような散布図を描いてデータの全体像を見ておきます。散布図の描き方については、この連載の第12回で既に見ましたが、おさらいをかねて手順を示しておきます。その後、回帰式で表される直線（近似曲線）を描画し、さらに、回帰式を直線の近くに表示してみましょう。

　相関係数は、セルK2にあらかじめ「=CORREL(I2:I171,F2:F171)」と入力して求められており、0.378...という値になっています（弱い正の相関）。ある程度直線的な関係があるものと考えられます。

　では、サンプルファイルをこちらからダウンロードして［中古車価格］ワークシートを開き、図2の後に記した箇条書きの手順に従って取り組んでみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

　この手順と次の「関数を使って回帰式の係数と定数項を求める」の手順については動画も用意してあります。操作方法を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。

動画1　Excelで回帰分析（線形回帰）の回帰式を可視化／計算するには

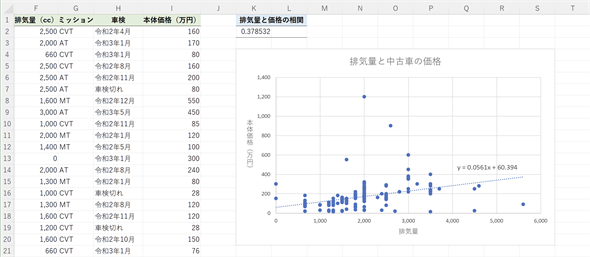図2　中古車データの回帰式を可視化する
散布図には回帰式で表される近似曲線を表示することができる。また、回帰式も表示できる。外れ値が幾つかあるように見えるので、それらのデータを除外すると回帰式の当てはまりがよくなりそうである（が、そのための前処理については後述する）。回帰式はy＝0.0561x＋60.394であることが分かる。つまり係数aが0.0561、定数項bが60.394となる。

　手順は以下の通りです。排気量のデータはセルF1〜F171に、本体価格のデータはセルI1〜I171に入力されています。セルF1とセルI1には見出しが入力されているので、値は2〜171行目の170件となります。

Excelでの操作手順

• セルF1〜F171とセルI1〜I171を選択する
• ［挿入］タブを開き、［散布図（X, Y）またはバブルチャートの挿入］ボタンをクリックする
• ［散布図］を選択する（これで散布図が作成される）
• 系列（作成された散布図のいずれかの点）を右クリックし、［近似曲線の追加］を選択する
• ［近似曲線の書式設定］作業ウィンドウで［グラフに数式を表示する］チェックボックスをオンにする

Googleスプレッドシートでの操作手順

• セルF1〜F171とセルI1〜I171を選択する
• メニューバーから［挿入］−［グラフ］を選択する
• ［グラフエディタ］作業ウインドウで［グラフの種類］リストから［散布図］を選択する（これで散布図が作成される）
• ［グラフエディタ］作業ウインドウで［カスタマイズ］をクリックする
• ［系列］をクリックして下位の設定項目を表示し、［トレンドライン］チェックボックスをオンにする
• ［ラベル］のリストから［方程式を使用］を選択する

　グラフ化するセルの範囲を選択するには、ドラッグ操作と［Ctrl］＋ドラッグ操作で離れた範囲を選択するよりも［名前］ボックスに「F1:F171,I1:I171」と入力する方が簡単です。ただし、Googleスプレッドシートでは、この指定ができないので、［名前］ボックスに「F1:F171」と入力した後、［Ctrl］キーを押しながらセルI1〜I171をドラッグする必要があります。

　回帰式の係数aは、直線の傾きを表すので、排気量が1cc大きくなると本体価格は0.0561万円（＝561円）だけ上がることが分かります。定数項はxの値、つまり排気量が0（エンジンがない）のときの本体価格ということになります。この例では年式や車検などについては考慮しておらず、車体の価値が排気量だけで決まるという前提なので、定数項の値の60.394（万円）は車体に価値がないときにも必要な固定費と考えることができます。

回帰式の係数と定数項を求めよう

　散布図には回帰式も表示できるので、回帰式の係数aや定数項bがいくらであるかも分かります。y＝ax＋bのxに、排気量の値を代入すれば、本体価格yが予測できますね。しかし、グラフからaとbの値を読み取り、セルに入力して計算するのはあまり賢明な方法とはいえません。出力結果を手作業で入力し直すのは手間がかかるだけでなく、ミスの原因ともなるからです。そこで、関数を使って回帰式の係数aと定数項bを求めることにしましょう。

　回帰式y＝ax＋bの係数aを求めるにはSLOPE関数を使い、定数項bを求めるにはINTERCEPT関数を使います。引数には、既に分かっている目的変数yの値（既知のy）と既に分かっている説明変数xの値（既知のx）を指定します。同じサンプルファイルの［単回帰分析］ワークシートを開き、図3のようにSLOPE関数とINTERCEPT関数を入力してみましょう。排気量の値（既知のx）はセルF2〜F171に、それぞれの本体価格（既知のy）はセルI2〜I171に入力されています。手順は図の中にも記してありますが、図の後にも箇条書きで記しておきます。

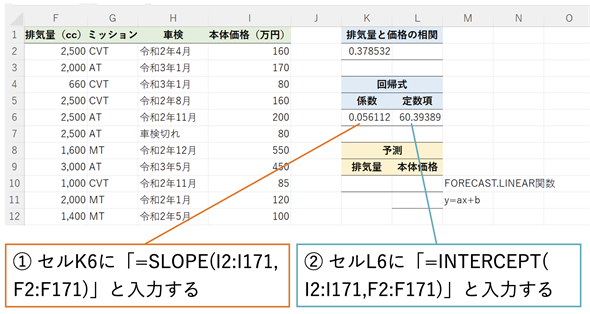図3　回帰式の係数と定数項を求める
SLOPE関数を使って回帰式の係数を求め、INTERCEPT関数を使って定数項を求める。いずれも、引数には既に分かっている目的変数yの値（既知のy）と、既に分かっている説明変数xの値（既知のx）を指定する。

　手順は以下の通りです。

• セルK6に「=SLOPE(I2:I171,F2:F171)」と入力する
• セルL6に「=INTERCEPT(I2:I171,F2:F171)」と入力する

　図3から、回帰式は以下のようになることが分かります。散布図に表示された値よりも詳細な値が求められていますね（小数点以下の表示桁数を増やせば、有効数字15桁まで表示できます）。

回帰式を利用した予測を行ってみよう

　続いて、回帰式を利用した予測を行います。例えば、排気量が1500ccの場合、x＝1500なので、本体価格は以下のようになります。

　しかし、このような数式を使って自分で計算しなくても、FORECAST.LINEAR関数を使えば、予測に使いたいxの値と、既知のyの値、既知のxの値を指定するだけで、予測値が求められます（図4）

図4　排気量から中古車の価格を予測する
セルL10ではFORECAST.LINEAR関数を使って予測値を求めている。一方、セルL11では回帰式に値を代入して予測値を求めている。当然のことながらこれらの値は一致する。上で見た計算とは答えが異なるのは係数や定数項の小数点以下の桁数の違いによるもの。

　手順は以下の通りです。

• セルK10に「1500」と入力する
• セルL10に「=FORECAST.LINEAR(K10,I2:I171,F2:F171)」と入力する
• セルL11に「=K6*K10+L6」と入力する

　ここまでは「習うより慣れろ」主義で、取りあえず回帰分析を行ってみました。しかし、回帰分析の仕組みについてはあまり詳しくはお話ししていませんでした。最初に、回帰式は各データの近くを通る直線であるとお話ししましたが、「近くを通る」の意味をきちんと見ておきましょう。

回帰分析の考え方（単回帰分析の場合）

　回帰式の意味を図5で考えてみます（話を簡単にするためにこれまでのデータとは少し違う値を使っています）。回帰式は目的変数のそれぞれの値（実測値）と直線（予測値）との誤差ができるだけ小さくなるように係数aと定数項bを決めたものです。ここでは考え方が分かればいいので、aとbの値を求めるための道筋を示すにとどめます。

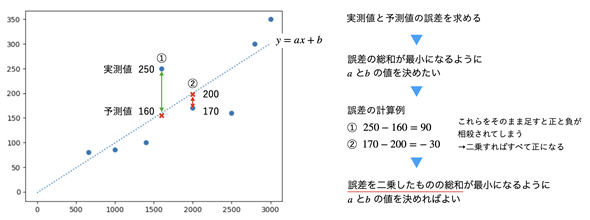図5　回帰式の意味（係数と定数項の求め方）
実測値は●で表された点、予測値は回帰式で表される直線上の×点。それぞれの実測値と予測値の差（誤差）の合計が最小になるようにaとbの値を決めたい。ただし、誤差は正の値になることも負の値になることもあるので、単純に合計を求めるとそれらの値が相殺されてしまう。そこで、誤差の絶対値を求めるために誤差を二乗しておく。その合計が最小になるようにaとbの値を決めればよい。

　図5の意味を確認しながら進めるために、以下の穴埋めの部分を考えてみてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

　例えば、左から4番目の点を見てみましょう。実際には1600ccの中古車が250万円であったとします。単位の万円を省略して表すと、実測値は　250　です。ここで、回帰式y＝ax＋bにx＝1600を代入してみたところ、予測値がy＝160になったとします。すると実測値と予測値の差は250−　160　＝　90　です。これは正の値ですね。

　左から5番目の点についても見てみましょう。2000ccの中古車の本体価格、つまり実測値は　170　です。回帰式y＝ax＋bにx＝2000を代入したところ、予測値がy＝200になったとします。実測値と予測値の差は、170−　200　＝　-30　です。こちらは負の値になります。

　実測値と予測値の誤差を最小にするには、それぞれの誤差を全て足した合計が最小になるようにすればいいですね。しかし、上で求めたように誤差は正になることもあれば負になることもあるので、そのまま足してしまうと正の値と負の値が相殺されてしまいます。そこで、誤差を二乗して全て正の値にします。そして、その総和が最小になるようなaとbの値を求めます。つまり、誤差の二乗和を最小にするようにaとbの値を決めるというわけです。このような方法を最小二乗法と呼びます。

　ここでは、実測値と予測値の誤差の二乗和を最小にするaとbの値を求めればいい、というところまでたどり着ければ十分です。それぞれの値を求めるための計算はSLOPE関数とINTERCEPT関数に任せることにしましょう。

　SLOPE関数とINTERCEPT関数を使えば回帰式の係数aと定数項bの値が簡単に求められますが、上の説明だけでは物足りない（SLOPE関数やINTERCEPT関数で実際にどのように計算されているのかが気になる）という方もいると思います。結果だけ示しておくと以下のようになります。

　なぜこのような式で求められるのか興味のある方は、こちらのリンク先に詳しい話を掲載しているので、ぜひご参照ください。微分（偏微分）の知識が必要になりますが、基本的に四則演算のみで理解できます。

回帰分析の精度を上げるには

　最初に述べたように、回帰分析には、適切に分析するための準備が必要です。その際に留意すべきポイントを2点挙げておきます。他にも考慮すべきことはあるのですが、今回はこの2つに絞って見ておきましょう。

• 変数同士にどのような関係があるかを見極める（モデルの選択）
• 外れ値や欠損値などがないかどうか調べる（データクリーニング）

　これまでは、説明変数と目的変数が直線的な関係であるという前提で、線形回帰モデル（y＝ax＋bなどの一次式で表される回帰式）を利用した例を見てきましたが、相関係数を求めたり、散布図を描いてみたりすると「関係はあるが直線的な関係ではない」と考えられる場合もあります。そのような場合には、最初に少し触れた指数回帰（y＝b＋a^x）や、次回お話しする予定の多項式回帰（y＝ax²＋bx＋cなど二次以上の項があるもの）など、より適切と考えられるモデルを利用します。ただ、今回の中古車データの例に関しては、線形回帰モデルで進めることにします。

　外れ値の発見については、散布図が役に立ちます。この連載の第10回で紹介した箱ひげ図や、第4回で紹介したスミルノフ・グラブス検定なども使えます。

　散布図の中で特に目立つ1200万円と900万円の中古車は、プレミアの付いた希少価値のある旧車です（元のデータでは81行目と105行目にあります）。また、排気量が0の中古車はEV（電気自動車）です（13行目と68行目にあります）。これらの値を除外すると、より直線的な関係になりそうですね。

　この例には欠損値は存在しませんが、CORREL関数、SLOPE関数、INTERCEPT関数、FORECAST.LINEAR関数では、説明変数または目的変数の値が存在しないペアや、文字列が入力されているセルは無視されるので、欠損値があっても、存在するデータだけで計算が行われます。ただし、欠損値があることを確認しておくことは重要です。

　では、外れ値を除外したデータで回帰分析を行ってみましょう。［外れ値の除外］ワークシートを開いて取り組んでみてください。データを4行削除したので、目的変数はセルI2〜I167、説明変数はセルF2〜F167となります。手順はこれまでと全く同じです（図6）。

図6　排気量から中古車の価格を予測する（外れ値を除去した例）
入力すべき関数はこれまでに見たものばかり。引数として指定するセル範囲が異なるだけ。相関係数が0.516...となっており、最初に見た例よりも直線的な関係になっていることが分かる。極端に大きな本体価格の影響を受けなくなったので、予測値は少し小さくなっている。

　手順は以下の通りです。セルK2にはあらかじめ「=CORREL(I2:I167,F2:F167)」と入力されています。

• セルK6に「=SLOPE(I2:I167,F2:F167)」と入力する
• セルL6に「=INTERCEPT(I2:I167,F2:F167)」と入力する
• セルK10に「1500」と入力する
• セルL10に「=FORECAST.LINEAR(K10,I2:I167,F2:F167)」と入力する

　最初に見た例（図5）では、相関係数は0.378...と弱い正の相関になっていますが、外れ値を除外すると0.516...となり、正の相関が少し強くなります。

回帰分析の精度を評価するには

　回帰分析の精度を評価するためにはR²（決定係数）やRMSE（二乗平均平方根誤差）などが使われます。単回帰分析の場合、決定係数は相関係数の二乗で求められます。決定係数は値が大きいほど精度が良く、RMSEは値が小さいほど精度が良いと考えられます。RMSEを求めるための式は以下の通りです。

　差の二乗和を求めるには、SUMXMY2関数が使えるので、どのセルでもいいので「=SQRT(SUMXMY2(I2:I167, K6*F2:F167+L6)/COUNT(I2:I167))」と入力してみてください。Googleスプレッドｰシートでは、「=ARRAYFORMULA(SQRT(SUMXMY2(I2:I167, K6*F2:F167+L6)/COUNT(I2:I167)))」と入力してください。RMSEの値は84.657...となります。

　ちなみに、最初の例であれば、［単回帰分析］ワークシートで「=SQRT(SUMXMY2(I2:I171, K6*F2:F171+L6)/COUNT(I2:I171))」と入力します。Googleスプレッドｰシートでは、「=ARRAYFORMULA(SQRT(SUMXMY2(I2:I171, K6*F2:F171+L6)/COUNT(I2:I171)))」と入力してください。RMSEの値は128.734...となります。

　RMSE値を比べると、外れ値を除外したことにより、精度が上がっていることが分かりますね。

　Excelの散布図では［近似曲線の書式設定］作業ウィンドウで［グラフにR-2値を表示する］チェックボックスをオンにすると、近似曲線の近くに決定係数が表示されます。Googleスプレッドｰシートでは、［グラフエディタ］作業ウインドウの［カスタマイズ］画面で［系列］の下の［決定係数を表示する］チェックボックスをオンにします。

説明変数と目的変数の関係が直線的でない場合 〜 指数回帰の例

　最初に触れたように、回帰式は直線を表すような式でなくても構いません。回帰分析に先立って散布図を作成したところ、xの値が大きくなるとyの値が急激に大きくなるように見えたとしましょう。そのような場合には、以下のような指数関数を回帰式とした方が適切な場合があります。例えば、細菌の増殖や感染者数の増加などの例がそれに当たります。

　ただし、細菌や感染者数はある程度増えると、その先は増加率が低下します。そのようなモデルを表すにはロジスティック方程式がよく使われます。ただ、今回の話題からは外れてしまうので、ここでは指数回帰のみを取り扱います。後のコラムで説明するように、変曲点（増加率が減少に転じる点）より前の部分では、ロジスティック方程式（の解であるロジスティック関数）を指数関数で近似できます。

　指数回帰の場合、LOGEST関数を使えば定数bや底aを一度に求めることができます（yの対数を求めて、これまでに見たような回帰分析を行っても構いませんが計算は少し面倒です）。図7の例は2020年1月16日〜2023年5月8日（5類感染症に移行した日）までの新型コロナウイルス感染症新規陽性者数の累計データです。このデータは厚生労働省のオープンデータの「新規陽性者数の推移（日別）」を基に作成したものです。

　サンプルファイルをこちらからダウンロードして［陽性者数の累計］ワークシートを開き、回帰式の底aと定数bを求め、散布図を描いて近似曲線を追加してみましょう。図7の後に示した手順に従って進めてみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。なお、この手順については動画も用意してあります。操作方法を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。

動画2　Excelで回帰分析（指数回帰）の回帰式を可視化／計算するには

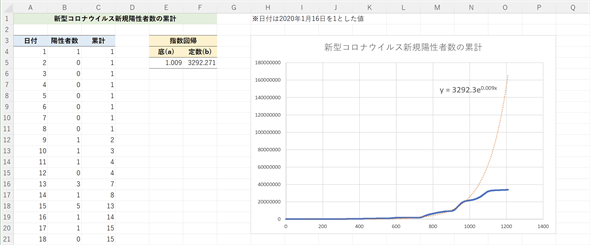図7　新型コロナウイルス感染症新規陽性者数の累計を予測する
回帰式はy＝3292.271× 1.009^xとなっている。散布図の青い●は実測値（間隔が狭いので線に見えている）、赤の点線は回帰式を元に描いた近似曲線。ただし、散布図には底をe＝2.71828...としたy＝3292.3× e^0.009xが回帰式として表示されている（a^x＝e^cxとするとc＝log_eaで求められる）。

　図7は以下の手順で作成されています。A列は日付のシリアル値をそのまま使ってもいいのですが、実際に計算すると、定数項があまりにも小さくなって見づらいので、2020年1月16日を1とした値にしてあります。これが説明変数xに当たり、C列の累計が目的変数yに当たります。データは1212行目まで入力されています。

回帰式の係数と底の計算

• セルE5に「=LOGEST(C4:C1212,A4:A1212,TRUE,FALSE)」と入力する
  • スピル機能が使えない場合は、あらかじめセルE5〜F5を選択しておき、「=LOGEST(C4:C1212,A4:A1212,TRUE,FALSE)」と入力して、入力終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

近似曲線の描画

Excelでの操作手順

• セルA3〜A1212とセルC3〜C1212を選択して散布図を描画する
• 系列（作成された散布図のいずれかの点）を右クリックし、［近似曲線の追加］を選択する
• ［近似曲線の書式設定］作業ウィンドウで［指数回帰］オプション（または［指数近似］オプション）をオンにする
• ［グラフに数式を表示する(E)］チェックボックスをオンにする

Googleスプレッドシートでの操作手順

• セルA3〜A1212とセルC3〜C1212を選択して散布図を描画する
  • ただし、離れた範囲が選択しづらいので、セルA3〜C1212を選択して散布図を作成し、後でB列の系列を削除した方が簡単
• ［グラフエディタ］作業ウインドウで［カスタマイズ］をクリックする
• ［系列］をクリックして下位の設定項目を表示し、［トレンドライン］チェックボックスをオンにする
• ［種類］のリストから［指数関数］を選択する
• ［ラベル］のリストから［方程式を使用］を選択する

　なお、Googleスプレッドシートでは、LOGEST関数で求められる回帰式の定数と底はExcelで求めた値と同じですが、近似曲線は実測値に近くなるように表示されるようです（この例ではy＝81796× e^0.00533xとなります）。Googleスプレッドシートのサンプルファイルには、LOGEST関数で求められた回帰式による予測値もプロットしてあります（Excelの近似曲線と同様のものになります）。

　最後に、話がそれてしまいますが、今回使ったデータの性質に関連のあるちょっと発展的なお話をコラムとして掲載しておきます。

コラム　細菌の数や感染者数などはロジスティック方程式でモデル化される

　細菌の数や感染者数などはある程度増加すると増加率が低下していきます。そのような例を表すモデルとしてはロジスティック方程式がよく知られています。例えば、ロジスティック関数の特殊な形であるシグモイド関数の式は以下の通りです。目的変数yは0〜1の値を取るので（確率なので）、以下の式ではpと表しています。

　図8はシグモイド関数のグラフです。増加率が低下していき、やがて一定のレベルに収束していく様子が分かりますね。上で見たサンプルファイルの［シグモイド関数］ワークシートにこの例が含まれています。シグモイド関数の値がB列に求められており、散布図（平滑線とマーカー）を作成してあります。

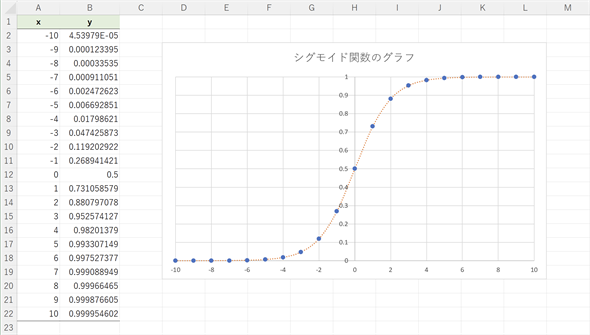図8　シグモイド関数の例
xの値が増えていくとyの増加率が増えていき、急激にyの値が大きくなるが、しばらくすると増加率が減少し、yの値が一定のレベルに収束する。シグモイド関数ではyの値は0〜1の範囲となる。なお、シグモイド関数の増加率が増えている部分（この例であれば-5〜0あたり）は指数関数で近似できる。

　入力されている数式は以下の通りです。EXP関数はeのべき乗を求める関数です。

• セルB2に「=1/(1+EXP(-A2:A22))」と入力する（シグモイド関数の値が求められる）
  • Googleスプレッドシートの場合は「=ARRAYFORMULA(1/(1+EXP(-A2:A22)))」と入力する

　図8を見ると、シグモイド関数の逆関数を使えば（yをxに変換すれば）直線的な値になることも分かりますね。シグモイド関数の逆関数は、以下のロジット関数と呼ばれるものです。対数は底がe＝2.7182...の自然対数です。

　例えば、セルC1に自然対数を求めるLN関数を使って「=LN(B2:B22/(1-B2:B22))」と入力すれば、元の-10〜10という値が得られます。

　既に述べたように、ロジスティック関数（シグモイド関数）の変曲点よりも前の部分は、指数関数で近似できます。サンプルファイルには、それらを比較したグラフも含めてあります。

　蛇足ながら、上で紹介したロジット関数とシグモイド関数を使えば、分類を行うためのロジスティック回帰の計算が簡単にできます。それについては、また機会があればお話ししたいと思います。

コラム　周期的に変化するデータには時系列分析が使える

　皆さんもご存じのように、陽性者数の増加には波があります。2022年の冬に第8波が来た後、しばらくは落ち着きを見せ、5類感染症になった2023年5月以降には第9波が来たと言われています。このように波があるデータを基に、その周期などを検出して予測するには、FORECAST.ETS関数による時系列分析が役に立ちます。なお、この関数を含めて以下の説明で用いる時系列分析の関数はExcelデスクトップ版でのみ利用でき、Microsoft 365オンラインやGoogleスプレッドシートでは利用できません。

　ここでは、波が比較的顕著に現れている2022年1月1日以降のデータのみを使い、使い方のみ紹介することにします。図9は、2023年5月9日から12月31日までの感染者数を予測した例です。Excel用の［時系列分析］ワークシートを開いて、数式やグラフを確認してみてください。

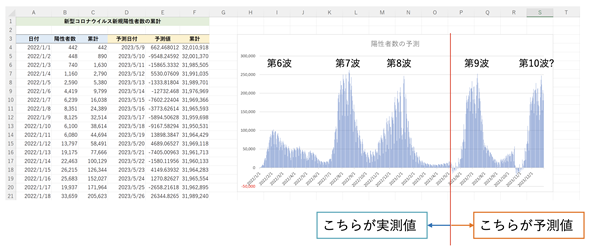図9　時系列分析による陽性者の累計の予測例
2023年1月1日〜5月8日の陽性者数を基に、2023年5月9日〜12月31日について予測してみた。2023年5月以降の第9波が予測できている。同じ周期で陽性者数が増えるのであれば、2023年12月以降にも陽性者数が増える予測になっている（実際、2024年に入って変異株JN.1への置き換わりが進んでおり、第10波が到来しているという声もある）。

　入力すべき関数は以下のたった1つだけです。

• セルE4に「=FORECAST.ETS(D4:D240,B4:B496,A4:A496)」と入力する

　予測を行いたい日付はセルD4〜D240に入力されています。予測の基となるデータ（陽性者数）はセルB4〜B496に入力されており、それに対するタイムライン（日付）はセルA4〜A496に入力されています。それらの値を指定して、E列で予測される陽性者数を求めているというわけです。

　右側のグラフはC列とE列を棒グラフにしたものです。離れた範囲を1つの系列とするのはちょっと難しいですが、以下のように、後から系列の範囲を追加する方法が簡単です。

• セルA3〜B496の範囲を選択して、取りあえず元のデータで棒グラフを作っておく
• 系列をクリックして選択し、数式バーに入力されている系列の指定を「=SERIES(時系列分析!$B$3,(時系列分析!$A$4:$A$733,時系列分析!$D$4:$D$240),(時系列分析!$B$4:$B$733,時系列分析!$E$4:$E$240),1)」に修正する

　図9を見ると、かなり正確に波（季節性）が予測できていることが分かります。なお、波の周期は、FORECAST.ETS.SEASONALITY関数で求められます。どのセルでも構わないので、「=FORECAST.ETS.SEASONALITY(B4:B496,A4:A496)」と入力すると、164という値が得られます。164日つまり5カ月半の周期で波が来ていることが分かります。

---

　今回は、単回帰分析により回帰式の係数と定数項を求めたり、回帰式を利用して予測したりする方法を紹介しました。また、回帰式を可視化するために、散布図に近似曲線を追加する方法についても触れました。しかし、事例として取り上げた中古車の価格は、排気量だけで決まるものではありません。

　そこで、次回は年式や走行距離なども含めた複数の説明変数を利用した回帰分析（重回帰分析）について見ていきます。数値として表されている値だけでなく、メーカーなどの文字列データ（カテゴリを表すデータ）も説明変数として取り扱ったり、新たな特徴量を作り出して説明変数に加えたりする方法についても触れます。さらに、前回見た気温と電気器具によるCO₂排出量のように、U字形の関係になっている場合にも回帰分析を行うために、多項式回帰を利用する方法も紹介します。次回も、どうぞお楽しみに！

関数リファレンス： この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

単回帰分析のために使った関数

SLOPE関数： 単回帰分析による回帰式の係数（直線の傾き）を求める

形式

SLOPE(既知のy, 既知のx)

引数

• 既知のy： 既に得られている目的変数の値（セル範囲）を指定する。
• 既知のx： 既に得られている説明変数の値（セル範囲）を指定する。

INTERCEPT関数： 単回帰分析による回帰式の定数項（切片）を求める

形式

INTERCEPT(既知のy, 既知のx)

引数

• 既知のy： 既に得られている目的変数の値（セル範囲）を指定する。
• 既知のx： 既に得られている説明変数の値（セル範囲）を指定する。

FORECAST.LINEAR関数： 単回帰分析による予測値を求める

形式

FORECAST.LINEAR(未知のx, 既知のy, 既知のx)

引数

• 未知のx： 予測に使いたい説明変数の値を指定する。このxに対するyの値が求められる。
• 既知のy： 既に得られている目的変数の値（セル範囲）を指定する。
• 既知のx： 既に得られている説明変数の値（セル範囲）を指定する。

指数回帰分析のために使った関数

LOGEST関数： 指数回帰による回帰式 y＝b×a^x の底aや定数項bを求める

形式

LOGEST(既知のy, 既知のx, [定数], [補正項])

引数

• 既知のy： 既に得られている目的変数の値（セル範囲）を指定する。
• 既知のx： 既に得られている説明変数の値（セル範囲）を指定する。
• 定数： 定数項bの値を求めるかどうかを以下の値で指定する。
  • TRUEまたは省略 …… bの値を求める
  • FALSE …… bの値を1とする
• 補正項： 検定などで使われる詳細な情報を求めるかどうかを以下の値で指定する。
  • TRUE …… 補正項を求める
  • FALSEまたは省略 …… 補正項は求めない（底と定数項のみを求める）

備考

　この関数は底と定数項などの値を一度に返すので、スピル機能が使えない場合は配列数式として入力する必要がある。また、説明変数xは複数あっても構わない。つまりy＝b×a₁^x₁×a₂^x₂× … ×a_n^x_nのような回帰式の底と定数項が求められる。返される値はa_n, ... , a₂, a₁, bの順であることに注意。

差の二乗和を求めるために使った関数

SUMXMY2関数： Σ(x_i−y_i)² の値を求める

形式

SUMXMY2(x, y)

引数

• x： xの値が入力されているセル範囲を指定する。
• y： yの値が入力されているセル範囲を指定する。

対数や指数を求めるために使った関数

LN関数： 自然対数を求める

形式

LN(数値)

引数

• 数値： 自然対数を求めたい値（真数）を指定する。自然対数の底はe＝2.71828...となる。

EXP関数： eⁿ を求める

形式

EXP(数値)

引数

• 数値： eの指数nに当たる値を指定する。自然対数e＝2.71828...のn乗が求められる。

時系列分析のために使った関数

FORECAST.ETS関数： 時系列分析を行う

形式

FORECAST.ETS(期日, 値, タイムライン, ［季節性］, ［補間］,［集計］)

引数

• 期日： 予測したい日付や時間などを指定する。
• 値： 既に分かっている値を指定する。
• タイムライン： 値に対する日付や時間などを指定する。
• 季節性： 周期を計算するかどうかを指定する。
  • 0： …… 季節性がないものと見なす。
  • 1または省略： …… 周期を自動的に計算する。
  • その他の値： …… 指定した値を周期とする。
• 補間： 欠損値の取り扱いを以下の値で指定する。
  • 0 …… 欠損値を0とする。
  • 1または省略： …… 隣接するセルの平均で補間する。
• 集計： タイムラインに同じ日付や時刻の値がある場合にどの手法で集計するかを以下の値で指定する。
  • 1または省略 …… 平均値（AVERAGE）
  • 2 …… 数値（＝数値を含むセル）の個数（COUNT）
  • 3 …… データ（＝空白ではない全てのセル）の個数（COUNTA）
  • 4 …… 最大値（MAX）
  • 5 …… 中央値（MEDIAN）
  • 6 …… 最小値（MIN）
  • 7 …… 合計（SUM）

備考

　この関数はExcelデスクトップ版（Excel 2016以降）でのみ利用でき、Microsoft 365オンラインやGoogleスプレッドシートでは利用できない。

FORECAST.ETS.SEASONALITY関数： 季節性の周期を求める

形式

FORECAST.ET.SEASONALITY(値, タイムライン, ［補間］,［集計］)

引数

• 値： 既に分かっている値を指定する。
• タイムライン： 値に対する日付や時間などを指定する。
• 補間： 欠損値の取り扱いを以下の値で指定する。
  • 0 …… 欠損値を0とする。
  • 1または省略 …… 隣接するセルの平均で補間する。
• 集計： タイムラインに同じ日付や時刻の値がある場合にどの手法で集計するかを以下の値で指定する。
  • 1または省略 …… 平均値（AVERAGE）
  • 2 …… 数値（＝数値を含むセル）の個数（COUNT）
  • 3 …… データ（＝空白ではない全てのセル）の個数（COUNTA）
  • 4 …… 最大値（MAX）
  • 5 …… 中央値（MEDIAN）
  • 6 …… 最小値（MIN）
  • 7 …… 合計（SUM）

備考

　この関数はExcelデスクトップ版（Excel 2016以降）でのみ利用でき、Microsoft 365オンラインやGoogleスプレッドシートでは利用できない。

「やさしいデータ分析」