大相撲のアノーマリー (2):実践! Rで学ぶ統計解析の基礎(8)(2/2 ページ)
バブル上にいる力士
まず、Duggan&Levittでは、その八百長判定にどういう解析を用いているかということを簡単に説明します。Duggan&Levitt2002では、最初に「バブル上の力士」という概念を導入します。大相撲では1場所あたり15回の取り組みがあるのですが、先に8勝するとその力士は勝ち越ししたということで、番付が上がる可能性が大きくなります。番付が上がると待遇や評判が上がるので、力士は場所ごとに8勝することを目指すインセンティブを持っていることは明白です。ここから8勝に至らないギリギリの状態にいる力士を「バブル上の力士」とします。つまり、15日目の取り組みを迎えるときに7つの勝星を持っている力士は「バブル上の力士」です。同様に14日目の取り組みを迎えるときに、7勝の力士も6勝の力士も「バブル上の力士」です。14日目で6勝の力士はこの日に勝って、再び15日目で勝たなければ勝ち越せないということです。このバブル上の力士かどうかという判定基準を表にまとめておきました。
この判定基準でバブル上の力士を全データについて探し出します。具体的な例を提示しましょう。1999年1月場所の千秋楽で武蔵丸は貴乃花と対戦しますが、このときは前日までに7勝だったので、この状態の武蔵丸はバブル上の力士であるといえます。
rikishi vs win year month day bubcand bub 46 武蔵丸 栃東 0 1999 1 1 0 0 47 武蔵丸 貴闘力 1 1999 1 2 0 0 48 武蔵丸 土佐ノ海 1 1999 1 3 0 0 49 武蔵丸 安芸乃島 1 1999 1 4 0 0 50 武蔵丸 魁皇 0 1999 1 5 0 0 51 武蔵丸 玉春日 0 1999 1 6 0 0 52 武蔵丸 琴錦 0 1999 1 7 0 0 53 武蔵丸 蒼樹山 1 1999 1 8 0 0 54 武蔵丸 琴乃若 0 1999 1 9 1 0 55 武蔵丸 湊富士 1 1999 1 10 1 0 56 武蔵丸 千代大海 0 1999 1 11 1 1 57 武蔵丸 時津海 1 1999 1 12 1 1 58 武蔵丸 貴ノ浪 1 1999 1 13 1 0 59 武蔵丸 若乃花 0 1999 1 14 1 1 60 武蔵丸 貴乃花 1 1999 1 15 1 1
さて、すべての取り組みについて上記のバブル判定基準に基づいてバブル上の力士を判定します。その後に、その力士と対戦する相手の力士がバブルかバブルでないかによる判断を加味しなければなりません。その理由は、もし双方の力士がバブル上にあるならば、どちらも勝ち越しを目指して勝負をするでしょうから、八百長が起きる可能性が低いと判断すべきだからです。その反対に、バブル上の力士の対戦相手がバブル上にない、つまりまだ負けに余裕があるときや勝ち越しているときは、対戦相手が自分の星を売買の対象とするインセンティブが働くことが考えられますので、この対戦はバブル上にあるとします。
バブルの判定ができた後は、バブル上の力士が勝ちやすいかどうかを統計学的に確かめます。これには次のようにします。まず、バブルとバブルでない者同士の対戦には、それぞれ1と-1という数値を割り振ります。バブル同士の対戦、バブルでない者同士の対戦には、双方に0という数値を割り当てます。一方、バブル、バブルでないに関わらず力士が勝つ場合は1、敗ける場合には0という数値を割り当てます。このようにすると、すべての場所のすべての取り組みでバブルフラグが-1、0、1、勝ちフラグが1、0と割り当てられたことになります。これを図示すると、以下の通りです。
図の横軸はバブルフラグ、縦軸は勝ちフラグで、可能性のある点にはAからFまでの6つのアルファベットを振っています。バブル同士の対戦、バブルでない同士の対戦はF点またはC点にランダムに分布します。バブルの力士とバブルでない力士の対戦はA-DのペアかB-Eのペアに分かれるはずです。この場合のバブルフラグは必ず片方が1なら片方は必ず-1ですし、引き分け・休場は解析データから排除しますので、勝ち負けが明らかだからです。この状況で、もしもバブル上の力士が勝ちやすいならば、B-Eに点が集まりやすいということです。そのことは、FまたはCの点がランダムに分布すると仮定しても、B-Eに点が集まりやすいならば全体として正の相関が出ると予想できます。従って、勝ちフラグとバブルフラグの線形回帰をすれば、バブルの力士が勝ちやすいかどうかということが統計学的に確かめることができます。
バブル上の力士は勝ちやすいか?
このようにバブル判定をして、勝ちフラグとバブルフラグで線形回帰したソースコードを以下に置きました。今回は比較的煩雑な処理が多いので、ここではソースコードは細かくは提示せずに、ソースコードをダウンロードするようにしました。
ダウンロードしたソースコードを実行するには、ソースコードを保存したフォルダに移動して、Rを立ち上げ、以下のコマンドを実行します。実行には、取り組みデータをインターネットから落とすためにネットに接続した環境が必要です。また、筆者のiMac(3.06GHz Core 2Duo)で実行すると7分から8分ほどかかります。
> source("sumoregression.R")
このソースコードで実装したロジックは次の通りです。幕内71場所の対戦データに、bubという変数を作り、初期状態は0を設定しておきます。そして、すべての対戦ごとにバブルの判定を行い、対戦する力士のうち片方だけがバブルにある力士のbub変数に1を入れ、その対戦相手のbub変数に-1を入れます。対戦者両者がバブルにある場合は、どちらのbub変数も0のままにします。今回のコードではdf1というデータフレームにbub変数を作りました。また、幕内力士のうち、前頭の下の方の力士は十両の力士と対戦します。これについてYahoo!スポーツではデータを見つけることができませんでしたが、幕内力士の勝敗データの鏡像イメージとして、ある程度再現することができます。この場合に問題となるのは、十両力士がバブル上にあるかどうかが分からないということですが、ここではより計算結果をアノーマリーにシフトさせるように、幕内力士と対戦する十両力士は全員バブル上にないと仮定します。こうして計算した結果を再びデータフレームdf1とします。バブルフラグを計算したdf1は以下のようになります。
> head(df1) rikishi vs win year month day bubcand bub 1 貴乃花 琴錦 0 1999 1 1 0 0 2 貴乃花 土佐ノ海 0 1999 1 2 0 0 3 貴乃花 魁皇 1 1999 1 3 0 0 4 貴乃花 玉春日 0 1999 1 4 0 0 5 貴乃花 蒼樹山 1 1999 1 5 0 0 6 貴乃花 湊富士 1 1999 1 6 0 0
ちなみに、bubcand変数はbubを計算するための一時変数で、day変数は取り組み日です。
さて、バブル上の力士が勝ちやすいかどうかを統計学的に確かめるには、勝ちフラグとバブルフラグで線形回帰をし、その回帰係数が有意に正であることを確認する、というのがDuggan&Levitt2002の中心ロジックでした。ここではwin変数とbub変数について線形回帰します。それでは、Rで取り組み日ごとに、線形回帰を計算してみます。取り組み日ごとに線形回帰をするために、plyrライブラリのdlplyを利用しました。実行結果は次の通りです。
> lmf <- function(d) summary(lm(win ~ bub, d))
> dlply(df1, .(day), lmf)
...
$`11`
Call:
lm(formula = win ~ bub, data = d)
Residuals:
Min 1Q Median 3Q Max
-0.5190 -0.5022 0.4810 0.4978 0.5146
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.502204 0.009505 52.835 <2e-16 ***
bub -0.016821 0.016208 -1.038 0.299
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5001 on 2766 degrees of freedom
Multiple R-squared: 0.0003892, Adjusted R-squared: 2.785e-05
F-statistic: 1.077 on 1 and 2766 DF, p-value: 0.2994
$`12`
Call:
lm(formula = win ~ bub, data = d)
Residuals:
Min 1Q Median 3Q Max
-0.4969 -0.4960 -0.4951 0.5040 0.5049
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4960006 0.0095378 52.004 <2e-16 ***
bub -0.0008841 0.0149320 -0.059 0.953
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5002 on 2748 degrees of freedom
Multiple R-squared: 1.276e-06, Adjusted R-squared: -0.0003626
F-statistic: 0.003506 on 1 and 2748 DF, p-value: 0.9528
$`13`
Call:
lm(formula = win ~ bub, data = d)
Residuals:
Min 1Q Median 3Q Max
-0.5177 -0.4985 -0.4794 0.5015 0.5206
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.498514 0.009616 51.842 <2e-16 ***
bub 0.019146 0.014921 1.283 0.200
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5 on 2702 degrees of freedom
Multiple R-squared: 0.000609, Adjusted R-squared: 0.0002391
F-statistic: 1.647 on 1 and 2702 DF, p-value: 0.1995
$`14`
Call:
lm(formula = win ~ bub, data = d)
Residuals:
Min 1Q Median 3Q Max
-0.5746 -0.5038 0.4254 0.4962 0.5669
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.503826 0.009609 52.435 < 2e-16 ***
bub 0.070778 0.015201 4.656 3.38e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4982 on 2686 degrees of freedom
Multiple R-squared: 0.008007, Adjusted R-squared: 0.007637
F-statistic: 21.68 on 1 and 2686 DF, p-value: 3.379e-06
$`15`
Call:
lm(formula = win ~ bub, data = d)
Residuals:
Min 1Q Median 3Q Max
-0.6405 -0.4949 -0.3493 0.5051 0.6507
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.494893 0.009604 51.530 < 2e-16 ***
bub 0.145585 0.019429 7.493 9.1e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.495 on 2654 degrees of freedom
Multiple R-squared: 0.02072, Adjusted R-squared: 0.02035
F-statistic: 56.15 on 1 and 2654 DF, p-value: 9.094e-14
この線形回帰の結果を見ると、11日目、12日目、13日目の回帰係数に統計的に有意性を見出すことができません。14日目と千秋楽の回帰係数は統計的に有意な0.070778と、0.145585という結果になりますが、値が小さい上に、R二乗値も0.008と0.02という大きくない値です。
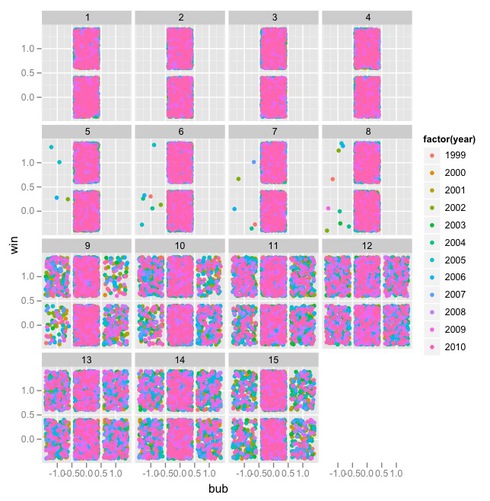
この回帰の元になったデータをビジュアル的に示すと次のようになります。
> ggplot(df1, aes(bub, win, color=factor(year))) + facet_wrap(~day) + geom_jitter()
図は15枚のファセットグラフで出来ています。それぞれのファセットは取り組み日を表しています。横軸がbub変数、縦軸がwin変数です。色は場所の年を表していますが、今回はあまり関係ありません。プロット点は本来なら1点に集中するべきものですが、それだと状況が分からないので、ggplot2のgeom_jitter()で散らしました。
どの取り組み日のファセットにもbub = 0のところはwinが1にも-1にも一様に分布していることが分かります。また、15日目以外はほぼ一様に分布していそうなことが分かりますが、千秋楽である15日目は、確かに右斜めの領域の分布が左斜めの領域の分布より濃くなっていますので、正の相関があると言えなくもなさそうです。
以上の結果から、バブル上の力士は千秋楽に勝ちやすいということは若干は言えるとかもしれません。つまり、1999年1月場所から、2010年9月場所までの71場所の幕内力士だけを見る限り、バブル上の力士が異常に高い勝率になるということは言えないが、千秋楽ではもしかすると勝ちやすいかもしれない、という消極的な主張になります。ですから、このことをもって八百長が存在しているとは、少し言いづらいかもしれません。
結局どうなの?
そもそも、データを大局的に見てみますと、幕内力士がバブル上にある対戦は12年間71場所中2983回で、1場所あたり42.01回になります。
> nrow(subset(df1, df1$bub==1)) [1] 2983 > nrow(subset(df1, df1$bub==1))/(12*6 - 1) [1] 42.01408
この対戦のうち、片方のみのバブルの力士が勝利したのが、1529回、1場所あたり、21.5回です。
> nrow(subset(df1, df1$win==1 & df1$bub==1)) [1] 1529 > nrow(subset(df1, df1$win==1 & df1$bub==1))/(12*6 - 1) [1] 21.53521
幕内力士および幕内で対戦した十両力士の12年間71場所において、バブル上の力士が勝利する平均勝率は0.51というように、実はバブル上の力士の勝率はランダムで対戦したときの勝率と同じ程度しかないのです。
> nrow(subset(df1, df1$win==1 & df1$bub==1))/nrow(subset(df1, df1$bub==1)) [1] 0.5125712
以上の結果見るとお分かりのように、今回の計算ではDuggan&Levitt2002のデータおよびその解析について、より消極的な主張しか言えません。言い換えると、Duggan&Levitt2002が成立している一番の根拠は、バブル上にある力士の勝率が高く、それが統計的に有意であるということろにあります。今回はその一番の根拠を積極的に確かめることができませんでした。
ただし、今回の計算においては、完全な十両力士の勝敗データを手に入れることができなかったので、それがバブル上の力士が勝ちやすいということがはっきりと示せなかった原因なのかもしれません。また2000年以降のマスコミによる八百長追求キャンペーンによって幕内力士内で八百長行為を防ぐ強いインセンティブが働いたのかもしれません(これについては、Duggan&Levitt2002のTable2においてマスコミの効果によってバブル上の力士が勝ちやすくなることがなくなるという主張がされています)。さらには、私の計算が誤っていることも考えられます。もしも、この計算の追試や、何らかの追加計算をされた方がいらっしゃったら、是非ともその結果を教えてくださることを熱望します。また、1999年以前10年間程度の十両・幕内の勝敗データを持っていらっしゃる方がおりましたら、そのデータを提供いただければ、より一層踏み込んだことが分析できると思います。そういったことについてのご連絡はknife@bakfoo.comにメールでお願いできればと思います。
そもそも、もともとのDuggan&Levitt2002の回帰分析においても回帰係数の値もR二乗値もそれほど大きくはないので、ベストセラーとなった「ヤバい経済学」(Freakonomics)で喧伝されたようなセンセーショナルな報告の仕方はどうなのかと、個人的には思ったりすることもないわけではありません。まあ、著者の2人はこの本でミリオネアになれたそうですから、その投資対効果は十分取れたということになるのでしょう。
また、Duggan&Levitt2002のTable3の計算は、バブル上にある力士とそうでない力士が13、14、15日目に対戦すると、バブル上の力士が勝ちやすく、その後同じ力士同士の対戦では先ほどのバブルで勝った力士が負けやすい、つまり勝星について返報性があることを示唆しています。これをもって、たとえ八百長が実際にないとしても力士の間の貸し借りは存在する、つまり、一度ワザと負けてあげればその後にお礼を返してもらうというやり取りの存在を示唆しています。しかし、これについても、なにぶんにも回帰係数の数値が小さすぎ、自然科学の基準からは疑問が残るようなものであると、個人的には思います。
まとめと次回について
このようにYahoo!スポーツにあるオープンデータを利用すれば、大相撲の勝敗にアノーマリーがあるのか、もっと具体的にいうと千秋楽付近でバブル上の力士が勝ちやすいかどうかということを定量的に調べることができます。結論は最近12年の幕内データを利用するだけでは、Duggan&Levitt2002が示したような八百長となるような根拠を積極的に見つけ出すことができない、というものでした。
次回もまた、オープンソースのRを利用して、オープンデータにアクセスし、オープンアイデアの活用をしたいと思います。次回は、Yahoo!スポーツの大相撲データを自動採取して、Google Refineで自動整形させるというスクリプトをどう実装するか、ということを示すことができればと思います。それでは、また会いましょう。
Index
大相撲のアノーマリー (2)
Page1
今回の前口上
大相撲八百長問題
オープンデータによる大相撲八百長問題の解析
Page2
バブル上にいる力士
バブル上の力士は勝ちやすいか?
結局どうなの?
まとめと次回について
関連記事
 いまさらアルゴリズムを学ぶ意味
いまさらアルゴリズムを学ぶ意味
コーディングに役立つ! アルゴリズムの基本(1) コンピュータに「3の倍数と3の付く数字」を判断させるにはどうしたらいいか。発想力を鍛えよう- Zope 3の魅力に迫る
Zope 3とは何ぞや?(1) Pythonで書かれたWebアプリケーションフレームワーク「Zope 3」。ほかのソフトウェアとは一体何が違っているのか? - 貧弱環境プログラミングのススメ
柴田 淳のコーディング天国 高性能なIT機器に囲まれた環境でコンピュータの動作原理に触れることは可能だろうか。貧弱なPC上にビットマップの直線をどうやって引く? - Haskellプログラミングの楽しみ方
のんびりHaskell(1) 関数型言語に分類されるHaskell。C言語などの手続き型言語とまったく異なるプログラミングの世界に踏み出してみよう  ちょっと変わったLisp入門
ちょっと変わったLisp入門
Gaucheでメタプログラミング(1) Lispの一種であるScheme。いくつかある処理系の中でも気軽にスクリプトを書けるGaucheでLispの世界を体験してみよう
Copyright © ITmedia, Inc. All Rights Reserved.

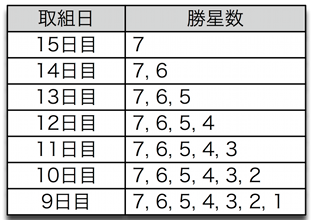 バブル上の力士の定義
バブル上の力士の定義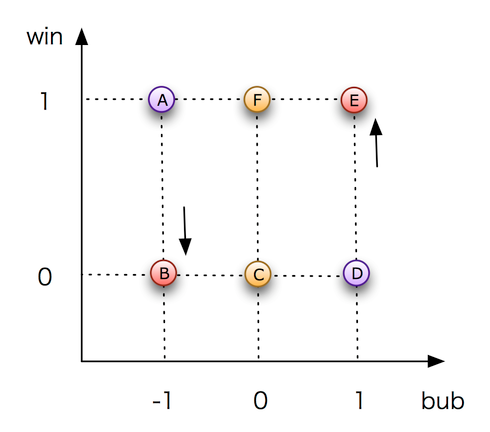 バブル上の力士が勝ちやすいならば、E、Bにデータが集まりやすい
バブル上の力士が勝ちやすいならば、E、Bにデータが集まりやすい