組み合わせテストを現場で使うときの判断指針とPDCA:現場で使うためのオールペア法、直交表の基本(4)(2/3 ページ)
組み合わせテストの手法をどのように選定するかを考えるヒント
次に、組み合わせテスト手法の選定方法について見ていきましょう。
組み合わせテストを実施する際、テストケースの生成方法をオールペア法にするか、直交表にするかを選択する前に、両者の比較を表1にまとめてみましょう。○×の記載は、二つの手法を比較した際に、より優れている部分を「○」、そうでないものを「×」と表現しています(以降で解説するように、×であっても必要があれば選択すべきところもあります)。
表1のテストの均等性の評価は、水準組み合わせが同数個の出現である直交表を○にしています。以降では、この比較表の各項目の詳細を見ていきましょう。
「網羅率」の比較:直交表の方が有利
「強さ+1の網羅率」はテスト回数がほぼ同じときに、想定し得る組み合わせが一回以上出現することを示す「網羅率」が高いかどうかのことです。オールペア法と比較した場合には直交表の方が網羅率が高くなる傾向性がありますので、表1では○にしています。
「強さ+1の分散」は網羅率と強い相関関係がありますが、この表では比較に入れています。ここで「強さ+1」の水準の組み合わせでの網羅率について、具体的な数値を見てみます。
オールペア法の「1回以上の出現」という網羅基準で、「強さ3」に設定した場合の組み合わせに対する網羅率を計算してみましょう。
例えば、「強さ2」の7因子3水準の直交表では、「強さ3」の網羅率は88.6%です。同様に「強さ2」の7因子3水準のオールペア法での「強さ3」の網羅率は最小で53.6%、テストケース数を直交表と同数にした場合でも80.6%と低くなっています(このあたりの比較が難しく感じられた場合は第二回の記事を思い返してみてください)。
また、「強さ3の水準組み合わせ」の分散(散らばり具合)は直交表の方が小さくなります。「分散が小さくなる」ということは、それだけ組み合わせテストが均等に実施できることを意味します。
これがどういう意味を持つかというと、直交表では「強さ2」で設定した場合でも、オールペア法と比較して「強さ3」の組み合わせに対する網羅率が100%に近いものになるということです。どちらを選択するかについては、この網羅率の差を有意と判断するか否かに懸かっています。
テスト回数の比較:オールペア法の方が少なくて済む
「テスト回数」の項目では、条件の緩いオールペア法の方が基本的には少ないので、○にしています。
しかし、「PICT」などの最小回数を保証しないテストケース生成ツールの実装では、直交表ツール「GaloisSoftTest」よりも多くのテストケースが生成されることがあります(両ツールの違い、使い方は第二回を参照ください)。
代表的なオールペア法ツールであるPICTで「最小回数の保証」を保証していませんので、表1では×にしています。一方、「水準数の制限」や「禁則処理」などはオールペア法に制限がありませんので○にしています。
つまり、どうすれば?
オールペア法か直交表の選択は、表1のように、組み合わせテストにおいて、
- (1-1)例えテストケース数を増加させても、
- (1-2)水準数をツールに合うように調整しても、
- (2-1)水準の組み合わせを均等にした方がいいのか、
- (2-2)より強い水準の組み合わせで網羅率が高い方がいいのか、
- (2-3)このときの出現の分散を小さくした方がいいのか、
で判断することになります。
直交表側から見ると、(1)群のデメリットと(2)群のメリットの比較と考えることができます。
もちろん、均一に出現し、より強い組み合わせの網羅率が高く、組み合わせの出現の分散も小さい直交表がテスト品質としては優れていますので、生成される「テストケース数にそれほど差がないときは直交表を用いた方がいい」でしょう。
このトレードオフはソフトウエアの性質に依存します。ハードウエアを伴う制御系や組み込み系ではテストも均一的にする方が望ましい場合が多いでしょう。一方、Webアプリケーションのようにソフトウエア中心で動作するシステムでは、論理的エラーを発見することに主眼を置くので、1回以上の組み合わせテストで十分かもしれません。ただし、Webアプリケーションでも、データの多種多様な状態をテストしなくてはいけないような非構造データを扱うビッグデータ処理などではハードウエアを伴うシステムと同様に、テストは均一になるようにした方がいいでしょう。
コストから逆算して手法を選択する方法
この判断も、コストからさかのぼって考えることができます。
この場合、直交表とオールペア法で、それぞれテストケースを生成してみて、テストケース数に大きな差がなければ直交表を用いて、大きな差があるときはトレードオフを考えてどちらかを選択するようにします。
判断は妥当だった?:手法と強さの決定のフィードバックによるPDCAサイクル
「オールペア法か直交表か」「強さをどうするか」をソフトウエアに応じて選定する方法を紹介してきましたが、その選定が妥当であったかどうかをきちんと振り返っておきましょう。
判断の妥当性を調べるために、コスト(テストケース数)と効果(欠陥の発見数)を計測し、その結果をフィードバックして、選定基準を見直していくのです。この流れを図2に示します。このPDCAサイクルを繰り返すことで、妥当な選定基準を作り上げていくのです。
関連記事
 いまさら聞けないTDD/BDD超入門(4):開発現場で保守性の高いTDD/BDDを実現するための3つのポイント――テストレベル/網羅性とは
いまさら聞けないTDD/BDD超入門(4):開発現場で保守性の高いTDD/BDDを実現するための3つのポイント――テストレベル/網羅性とは
開発現場でTDD/BDDを導入するためのポイントを大きく三つに分けて解説。テストレベルや網羅性、サイクルタイムについても紹介します。 テストエビデンス取得自動化の秘技(前編):Selenium VBAを使って自動でブラウザーを操作してスクショをExcelに張り付けてみた
テストエビデンス取得自動化の秘技(前編):Selenium VBAを使って自動でブラウザーを操作してスクショをExcelに張り付けてみた
システム開発におけるソフトウェアテスト(結合テスト〜システムテスト)において重要視されるエビデンス(作業記録)。前後編の2回にわたって、エビデンスとしてスクリーンショットをキャプチャし、テスト仕様書や納品書に張り付けていく作業を自動化するためのVBA/マクロのテクニックを紹介する。前編はSelenium VBAのインストール方法と使い方、スクリーンショットを自動でExcelに張り付ける方法について。 テスト自動化のROIを計算してみよう(1):テスト自動化の3つの目的とROIの必要性、定義
テスト自動化のROIを計算してみよう(1):テスト自動化の3つの目的とROIの必要性、定義
テスト自動化の導入理由や効果測定をROIという観点で説明できるように、テスト自動化のROIの概念から実際の計算式までを解説する連載です。
Copyright © ITmedia, Inc. All Rights Reserved.

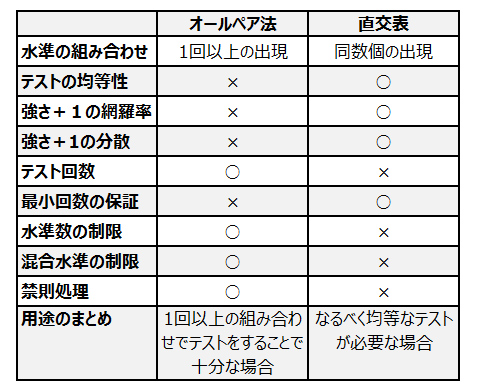 表1 オールペア法と直交表の比較
表1 オールペア法と直交表の比較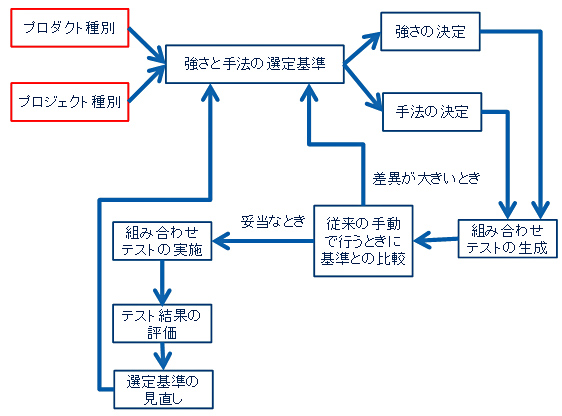 図2 選定基準のフィードバック
図2 選定基準のフィードバック



