まだまだ広く深い、暗号の世界――匿名認証や電子投票に利用される「ブラインド署名」「グループ署名」「ゼロ知識証明」：クラウド時代の暗号化技術論（8）（2/4 ページ）

[光成滋生，＠IT]

ゼロ知識証明

　「ゼロ知識証明」とは、ある人が自分の持っているある命題が真であることを、それ以外の情報を何も伝えずに相手に示す手法です。

　例えば、楕円曲線の点PとAさんの秘密鍵a、公開鍵Q=aPがあったときに、Aさんが秘密鍵aを持っていることをBさんに示すことを考えます。もちろん、aをそのままBさんに教えれば、BさんはaPがQに等しいかどうかを確認することでaが本物であることを検証できます。しかし当然、Aさんは秘密鍵aを教えたくはありません。このようなときに、相手に何も知識を与えずに、ある命題を知っていることを証明するのがゼロ知識証明です。

図4　対話的ゼロ知識証明と非対話ゼロ知識証明

　ゼロ知識証明には、証明したい相手と何度かやりとりをすることで証明する「対話的ゼロ知識証明」と、一度のやりとりで完結する「非対話ゼロ知識証明」があります。後者の方がプロトコルを組み立てる上では簡単になります。

ゼロ知識証明の例と満たすべき性質

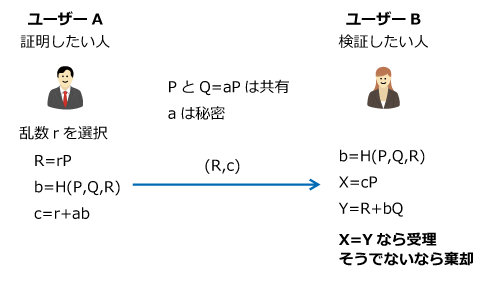
　楕円曲線の場合の非対話ゼロ知識証明を紹介しましょう。AさんとBさんは、PとQ=aPを共有している状態です。ハッシュ関数Hを用意します。

　Aさんは乱数rを作って、R=rPとb=H(P,Q,R)を計算します。それからc=r+abを求めて、(R,c)をBさんに渡します。

　Bさんは、b=H(P,Q,R)を計算します。そしてX=cPとY=R+bQを計算し、両者が等しいことを確認します。もしXとYが等しければ、Aさんが秘密鍵aを持っていると納得できます（受理）。そうでない場合は、Aさんはaを持っていないと判断します（棄却）。

図5　非対話ゼロ知識証明

　これでうまくいくことを確認しましょう。まず、Aさんが本当にaを知っている場合、Y=rP+baP=(r+ab)P＝cPなので、X=Yが成り立ちます。このように、Aさんがある命題を本当に知っているときに受理することを「完全性」といいます。

　逆に、Aさんが実はaを知らないのに、X=YとなるようにRやcの値を決められるでしょうか。X=YならR=cP-bQとなります。これを成立させようとすると、b=H(P,Q,R)となるように、うまくcの値を決めなくてはいけません。Hはハッシュ関数ですから、これはとても難しそうです。このように、Aさんがある命題を知らないときに受理できないことを「健全性」といいます。

　最後に、(R,c)からaの情報が漏れていないことを確認します。第2回で触れたように、「楕円離散対数問題は困難」だとすると、R=rPから、rを知ることはできません。よって、c=r+abからaを求めることはできません。厳密な証明はここでは省略しますが、このように情報が漏れていないことを「ゼロ知識性」といいます。

　ゼロ知識証明は、完全性、健全性、ゼロ知識性の三つの性質を満たしている必要があります。

　ところで今、楕円曲線の秘密鍵を知っていることを、ゼロ知識証明を用いて示す方法を紹介しました。一方、先に紹介した署名はあるメッセージを書いたのが確かに自分であることを相手に示す手法です。こう考えると両者はよく似ていますね。実際、ゼロ知識証明を使って署名を作ることも可能です。