Kerasを用いたディープラーニング（LSTM）による株価予測：ディープラーニング習得、次の一歩

ディープラーニングのチュートリアルが一通り終わったら、次に何をやる？今回は、誰にでも簡単にできる「株価予測」をテーマに、LSTMのニューラルネットワークを、Kerasを使って実装する方法を説明する。

» 2017年12月11日 05時00分公開

ご注意：本記事は、＠IT／Deep Insider編集部（デジタルアドバンテージ社）が「deepinsider.jp」というサイトから、内容を改変することなく、そのまま「＠IT」へと転載したものです。このため用字用語の統一ルールなどは＠ITのそれとは一致しません。あらかじめご了承ください。

誰でもディープラーニングの時代

　昨今、ディープラーニングの話を聞かない日はない。バズワードだった時期はとうに過ぎ、今や、実用化フェーズといっても過言ではない。

　しかし、ディープラーニングの原理自体は非常に単純である。本質は、n次元ベクトル空間内の点の集合を、超平面で仕切って見せることである。しかも、計算をやってくれるライブラリが、何種類も公開されている。TensorFlowなどがそうであるが、ここにきて、Kerasというさらにコーディングが簡単なライブラリが発表されており、個人ベースでのディープラーニングへの取り組みが、劇的に容易になっている。

　MNISTなどのチュートリアル、例題に取り組まれている読者の方も多いと考えているが、本稿はそういった皆さんを対象に、「手書き文字の分類はやってみたが、次は何をやろうか」というニーズに応えるため、企画されたものである。

　なお、Keras（バックグラウンドにTensorFlowを使用）や、Jupyter Notebookなどはインストール済みであることを前提とする。Python言語と、基本的なディープラーニング開発の知識も必要である。

なぜ株価予測なのか

　本当に株価が予測できれば、それこそ大変な功績であるが、はっきり言ってそれは幻想である。かのブラックショールズ方程式も、株価はランダムに変動するというモデルによって理論化されている。

　しかし、ざっくりレベルでよいのであれば、自宅PC上で翌日の日経平均終値騰落予測が、そこそこできるのである。予測に必要な過去の株価データはネット上に公開されており、誰でも容易に入手できる。しかも、1980年代くらいまでの高々数千件程度しかないため、学習もすぐ終わるので、パラメーターをいろいろ変えてその影響を見るということが、容易にできる。

　このように、株価予測というテーマは、誰にでも簡単にできて、ニューラルネットワーク構築上のノウハウ取得にも有益なテーマと言える。

本稿のゴール

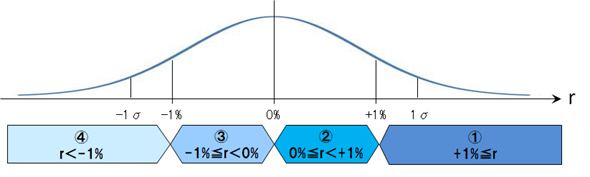
　翌営業日の日経平均終値に対する単純騰落予測（上がるか／下がるか）、および±1％以上／以下増減予測（全4パターン）を行う。騰落予測だけだと、応用上の利点はあまりない。やはり、どれくらい増減するのかが知りたいところであるが、閾値を決めてそれを超えるか超えないかを判定するようなモデルを採用することにより、増減予測を4択問題に帰着できる。増減率rと4択分類の関係を、図1に示す。

図1　増減率と4択分類の関係

　本稿では入力に時系列データを扱うため、ニューラルネットワークにLSTM（Long Short-Term Memory）を採用し、これをKerasを使って実装する。本稿の手法により、最終的に単純騰落予測は65％程度、増減予測のほうは45％程度の精度が実現できる。

株価データの入手と加工

　（米国の）Yahoo Financeなどから入手できる。Yahoo Financeの場合は、CSV形式でダウンロード可能である。例えば日経平均（N225）などのページを開き、［Time Period］欄で「Max」などを指定して［Apply］し、［Download Data］リンクをクリックすればダウンロードできる。

　ダウンロードしたファイルをExcelなどの表計算ソフトで開いてみると、取引の無い日付の行にnullが入っている。そのような行を削除しておく。

　次に、株価データ（取りあえず最初は「終値」を意味する［Close］列の値）の自然対数（ln）を取る。対数化する理由は、人間は大小比較を対数目盛で行っているためである（ex.音階）。

　さらに、前日の（対数）値との差分を取る。これにより、前日からの増減率（の対数表記）が得られる。

　こうして得られたデータは0.001オーダーの小さい値なので、これを100倍して見やすい値にする。

　これが学習データになる。データのレコード数をnとするとき、n行2列の表（1行目は見出し、1列目は日付、2列目が上記の計算値）が出来ているはずである。データ行数がn-1だが、これは前日差分を取る関係上、行数は1行減るからである。適当な名前を付けて(例：x-data.csv)、CSV形式でセーブしておく。

ラベルデータの作成

　上記の学習データから、ラベルデータを作成する。

　ln(1.01)×100＝0.995033085（閾値1％の対数表現）と学習データを比較して、4次元のone-hotベクトル*1を生成する。Excel上で関数をうまく使って*2、n-1行5列の表（1行目は見出し、1列目は日付、2～5列目は4次元のone-hotベクトル）を作成する。必ず「翌日」データからone-hotベクトルを生成すること。one-hotベクトルのデータ列の並び順は、1％以上（+1％ ≦ r）、0％以上（0％ ≦ r ＜ +1％）、-1％以上（-1％ ≦ r ＜ 0％）、-1％未満（r ＜ -1％）とする。

　翌日データから生成する関係上、行数がさらに1行減る。これも適当な名前を付けて（例：t-data.csv）、CSV形式でセーブしておく。

*1　one-hotとは、1つだけがHot（1）となり、それ以外はCold（0）となるような表現方法のこと。

*2　ヒントとして、例えば0％ ≦ r ＜ +1％が真のとき1で偽のとき0にするExcel関数は、rがB2セル（※翌日データはB3セル）の場合は=IF(AND(0.0<=B3, B3<0.995033085), 1, 0)のように表現できる。

CSVファイルの取り込み

　作成したCSVファイルをプログラムに読み込ませ、見出し行、日付列を外して、データを行列に展開する。学習データは(n-2,1)次行列、ラベルデータは(n-2,4)次行列になる。

　なお、参考情報として、筆者が実行したソースコードを以下に示す。これらをJupyter Notebook上で、コードブロック単位に実行した。CSVファイルは、Jupyter Notebookと同じフォルダーに置くこと。

　まず、各種import宣言である。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import csv

from __future__ import print_function
from keras.layers.core import Activation
from keras.layers.core import Dense
from keras.layers.core import Dropout
from keras.models import Sequential
from keras.utils import np_utils
from keras.utils import plot_model

from keras.layers.recurrent import LSTM
from keras.callbacks import EarlyStopping
from keras.initializers import glorot_uniform
from keras.initializers import orthogonal
from keras.initializers import TruncatedNormal

リスト1　import宣言

　次に、CSVファイルの読み込み処理である。

# 学習データ
df1 = csv.reader(open('x-data.csv', 'r'))
data1 = [ v for v in df1]
mat = np.array(data1)
mat2 = mat[1:] # 見出し行を外す
x_data = mat2[:, 1:].astype(np.float) # 2列目以降を抜き出してfloat変換
print('x_data.shape=', x_data.shape)

# ラベルデータ
# 1％以上／0％以上／-1％以上／-1％未満
df2 = csv.reader(open('t-data.csv', 'r'))
data2 = [ v for v in df2]
mat3 = np.array(data2)
mat4 = mat3[1:] # 見出し行を外す
t_data = mat4[:, 1:].astype(np.float) # 2列目以降を抜き出してfloat変換
print('t_data.shape=', t_data.shape)

リスト2　CSVファイル読み込み

学習データのテンソル化と、訓練データ／評価データ／テストデータへの分割

　まず、学習データをLSTM入力用のテンソルに変形する。内容説明は後から行うので、リスト3にざっと目を通してほしい。

maxlen = 80              # 入力系列数
n_in = x_data.shape[1]   # 学習データ（＝入力）の列数
n_out = t_data.shape[1] # ラベルデータ（=出力）の列数
len_seq = x_data.shape[0] - maxlen + 1
data = []
target = []
for i in range(0, len_seq):
data.append(x_data[i:i+maxlen, :])
target.append(t_data[i+maxlen-1, :])

x = np.array(data).reshape(len(data), maxlen, n_in)
t = np.array(target).reshape(len(data), n_out)

print(x.shape, t.shape)

# ここからソースコードの後半
n_train = int(len(data)*0.9)              # 訓練データ長
x_train,x_test = np.vsplit(x, [n_train]) # 学習データを訓練用とテスト用に分割
t_train,t_test = np.vsplit(t, [n_train]) # ラベルデータを訓練用とテスト用に分割

print(x_train.shape, x_test.shape, t_train.shape, t_test.shape)

リスト3　学習データのテンソル化とテストデータ分離

　上記で作成したx_dataオブジェクトから、基点を1行ずつずらしながらmaxlen行取り出し、それを1列に並べることで、学習データ行列x_dataの次元が(l, 1)であるとき、(l - maxlen + 1, maxlen, 1)次元のテンソルが出来る。このmaxlen変数は入力系列数、すなわち予測に使用する過去データの日数である。ここまでが、ソースコードの前半である。

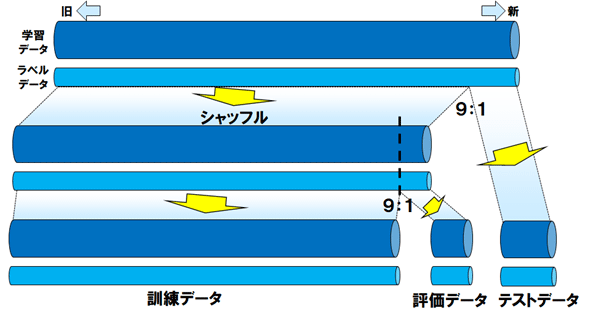
　ソースコードの後半は、訓練データ／評価データと、テストデータの分離である。この時点で学習データおよびラベルデータは日付の昇順に並んでいるが、それらを9：1に分割し、新しい方の1割をテストデータに充てる。

　9割の方はシャフルの上さらに9：1に分割し、それぞれ訓練データと評価データに充てるが、それはKerasのライブラリに実行させる（後掲のリスト4）。

　図2に、学習データ分割のイメージを示す。

図2　学習データ分割のイメージ

ニューラルネットワーク構築

　いよいよKerasのSequentialモデルを用いて、ニューラルネットワークを構築する。各種メソッドをそれこそレゴのように積み上げることで、簡単にネットワークを構築できる。

　重み行列の初期値は乱数で与えられるが、これが試行のたびに毎回同じになるように、乱数のseed指定を行う。また、ドロップアウトの比率は0.5に設定する。さらに、過学習を防ぐため、EarlyStopping（＝学習を適切なタイミングで早期に打ち切る機能）を使用する。

class Prediction :
def __init__(self, maxlen, n_hidden, n_in, n_out):
    self.maxlen = maxlen
    self.n_hidden = n_hidden
    self.n_in = n_in
    self.n_out = n_out

def create_model(self):
    model = Sequential()
    model.add(LSTM(self.n_hidden, batch_input_shape = (None, self.maxlen, self.n_in),
             kernel_initializer = glorot_uniform(seed=20170719),
             recurrent_initializer = orthogonal(gain=1.0, seed=20170719),
             dropout = 0.5,
             recurrent_dropout = 0.5))
    model.add(Dropout(0.5))
    model.add(Dense(self.n_out,
            kernel_initializer = glorot_uniform(seed=20170719)))
    model.add(Activation("softmax"))
    model.compile(loss="categorical_crossentropy", optimizer = "RMSprop", metrics = ['categorical_accuracy'])
    return model

# 学習
def train(self, x_train, t_train, batch_size, epochs) :
    early_stopping = EarlyStopping(patience=0, verbose=1)
    model = self.create_model()
    model.fit(x_train, t_train, batch_size = batch_size, epochs = epochs, verbose = 1,
          shuffle = True, callbacks = [early_stopping], validation_split = 0.1)
    return model

リスト4　ニューラルネットワーク本体

メイン処理

　上記で定義したニューラルネットワークを動かして、学習とテストを実施する。

　リスト5の前半は、上記のリスト4で定義したニューラルネットワーククラスのインスタンス生成と、学習、テストデータを使用した評価である。リストの後半は、単純騰落予測の的中率算出である。

　入力系列数（リスト4のmaxlen変数値）および出力次元数（以下のリスト5のn_hidden変数値）をいろいろ変化させて、予測精度がどのように変動するか、確認してみてほしい。

n_hidden = 80     # 出力次元
epochs = 100      # エポック数
batch_size = 10   # ミニバッチサイズ

# モデル定義
prediction = Prediction(maxlen, n_hidden, n_in, n_out)
# 学習
model = prediction.train(x_train, t_train, batch_size, epochs)
# テスト
score = model.evaluate(x_test, t_test, batch_size = batch_size, verbose = 1)
print("score:", score)

# 正答率、準正答率（騰落）集計
preds = model.predict(x_test)
correct = 0
semi_correct = 0
for i in range(len(preds)):
pred = np.argmax(preds[i,:])
tar = np.argmax(t_test[i,:])
if pred == tar :
    correct += 1
else :
    if pred+tar == 1 or pred+tar == 5 :
      semi_correct += 1

print("正答率:", 1.0 * correct / len(preds))
print("準正答率（騰落）:", 1.0 * (correct+semi_correct) / len(preds))

リスト5　メイン処理

入力データの種類の追加

　予測精度を改善するため、日経平均の始値（Open）、高値（High）、安値（Low）、およびNYダウ、ドル円、DAX指数、ハンセン指数、TOPIX、NASDAQ、SP500、上海総合指数を入力データに追加する。

　各種データをネットから入手し、日付をキーにExcelのvlookup関数を使うなどしてデータを1つのシートに統合する。これらのデータの中ではドル円データの量が最も少ないので、全体レコード数をこれに合わせる。また、東証が開いていて他市場が閉まっている場合には、その日の値がnullになっているので、その場合には前日の値を入れておく。

　これをCSV形式でセーブし、あとは上記と同様の手続きによって予測結果を確認してみてほしい。

patienceのチューニング

　EarlyStoppingにはpatienceというパラメーターがある（リスト4の後ろから5行目あたりを参照）。これは、学習打ち切り条件が発生したときに何回まで見逃すか、という値である。デフォルトは0であるが、いろいろ値を動かすと予測精度が改善する。他のパラメーターと併せて、チューニングを試してほしい。これらのチューニングにより、筆者の場合は冒頭に提示した数値まで、予測の精度を上げることができた。