挑戦！ word2vecで自然言語処理（Keras＋TensorFlow使用）：ディープラーニング習得、次の一歩（2/2 ページ）

[石垣哲郎，著]

ニューラルネットワーク構築

　ニューラルネットはKerasのSequentialモデルを用いて構築する。先に述べたように、本質的にはEmbeddingとDenseの2層だけである。

　学習の発散を防ぐため、EarlyStopping（＝学習を適切なタイミングで早期に打ち切る機能）を使用する。一般には評価データから算出される損失関数val_lossを監視対象にし、これが増加に転じたところで学習を停止させるが、今回の場合は評価データを使用しないことと、損失関数lossが減少を続けていても、正解率categorical_accuracyはかえって値が悪くなることがあるので、categorical_accuracyを監視対象に指定する。

　また、重み行列の初期値は乱数で与えられるが、これが試行のたびに毎回同じになるように、乱数のseed指定を行う。

class Prediction :
  def __init__(self, input_dim, output_dim):
    self.input_dim = input_dim
    self.output_dim = output_dim
            
  def create_model(self):
    model = Sequential()
    model.add(Embedding(self.input_dim, self.output_dim, input_length=1, embeddings_initializer=uniform(seed=20170719)))
    model.add(Flatten())
    model.add(Dense(self.input_dim, use_bias=False, kernel_initializer=glorot_uniform(seed=20170719)))
    model.add(Activation("softmax"))
    model.compile(loss="categorical_crossentropy", optimizer="RMSprop", metrics=['categorical_accuracy'])
    print('#2')
    return model
  
  # 学習
  def train(self, x_train, t_train,batch_size, epochs, maxlen, emb_param) :
    early_stopping = EarlyStopping(monitor='categorical_accuracy', patience=1, verbose=1)
    print ('#1', t_train.shape)
    model = self.create_model()
    #model.load_weights(emb_param)    # 埋め込みパラメーターセット。ファイルをロードして学習を再開したいときに有効にする
    print ('#3')
    model.fit(x_train, t_train, batch_size=batch_size, epochs=epochs, verbose=1,
          shuffle=True, callbacks=[early_stopping], validation_split=0.0)
    return model

リスト5　ニューラルネットワーク本体

メイン処理

　上記で定義したニューラルネットを動かして、学習を進める。入力次元数input_dimは単語数、出力次元数output_dimは埋め込みベクトルの次元数である。

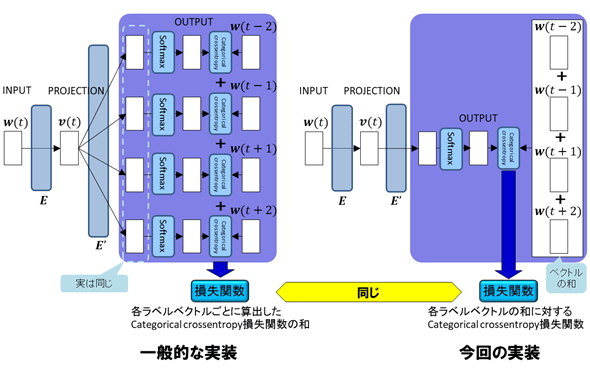
　今回はラベルデータ（すなわち予測単語）が複数あるので、ニューラルネットに渡すラベルデータに工夫を施す。図4にイメージを示す。

　1つの入力に対してn個のラベルベクトルがある場合、普通のやり方は図4の左側のように、それぞれのラベルベクトルごとにcategorical_crossentropy損失関数計算を合計n回行って、それらを足し込むことになる。すなわち、入力データ数がn倍になったのと同様の計算量が必要になる。

　ところが、入力ベクトルが同じなら、この計算はラベルベクトル側から見て線形である。したがって、図4の右側のように分配法則的に、n個のラベルベクトルを足し合わせた後でcategorical_crossentropy損失関数計算を行えば、その計算回数は1回で済む。

　この考えに従って、ラベルベクトルを「n-hotベクトル」的に整形して、訓練を実施する。変則的なやり方であるが、計算量が大幅に削減できるので、今回はこのやり方を採用した。

　なお、後で使えるように、学習済みのパラメーターをセーブしてある。

図4　ラベルデータ加工の考え方

vec_dim = 100
epochs = 10
batch_size = 200
input_dim = len(words)
output_dim = vec_dim

emb_param = 'param_skip_gram_2_1.hdf5'    # 学習済みパラメーターファイル名
prediction = Prediction(input_dim, output_dim)
row = t_train.shape[0]

t_one_hot = np.zeros((row, input_dim), dtype='int8')    # ラベルデータをN-hot化
for i in range(0, row) :
  for j in range(0, maxlen*2):
    t_one_hot[i, t_train[i,j]] = 1
  
x_train = x_train.reshape(row,1)
model = prediction.train(x_train, t_one_hot, batch_size, epochs, maxlen, emb_param)

model.save_weights(emb_param)           # 学習済みパラメーターセーブ

リスト5　メイン処理

評価

　埋め込み表現のベクトル演算を試してみる。実は、get_weights()やload_weights()、save_weights()で扱っているパラメーターファイルは、重み行列のリストになっている。この0番目の行列が埋め込み行列であり、i行目の行ベクトルがインデックスiの単語のベクトル表現になっている。したがって、埋め込み行列に各単語のone-hotベクトルを掛けることで、その単語の埋め込みベクトル表現を得ることができる。

　演算の結果がどの単語に近いのかは、「コサイン類似度」で評価する。コサイン類似度とは一言でいうと、2つのベクトルが見込む角度の余弦である。当然、値の範囲は-1から1で、1に近いほど（要は大きいほど）類似度が高いと評価する。

　以下のコードのwordX（X=0〜2）に試してみたい単語を記述し、実行すると、第5候補まで表示される。なお、語彙に無い単語を指定すると、エラーになる。

param_lstm = model.get_weights()
param = param_lstm[0]
word0 = '一'
word1 = '１'
word2 = '２'
vec0 = param[word_indices[word0],:]
vec1 = param[word_indices[word1],:]
vec2 = param[word_indices[word2],:]

vec = vec0 - vec1 + vec2
vec_norm = math.sqrt(np.dot(vec, vec))

w_list = [word_indices[word0], word_indices[word1], word_indices[word2]]
dist = -1.0
m = 0
for j in range(0, 5) :
  dist = -1.0
  m = 0
  for i in range(0, len(words)) :
    if i not in w_list :
      dist0 = np.dot(vec, param[i,:])
      dist0 = dist0 / vec_norm / math.sqrt(np.dot(param[i,:], param[i,:]))
      if dist < dist0 :
        dist = dist0
        m = i
  print('第' + str(j+1) + '候補:')
  print('コサイン類似度=', dist, ' ', m, ' ', indices_word[m])
  w_list.append(m)

リスト6　埋め込みベクトル演算の評価

　冒頭に記述したとおり、「一」 − 「１」 ＋ 「２」は「二」になる。ただし、算用数字は全角で指定すること。

　また、「一」 − 「１」 ＋ 「３」も「三」になった。

　しかし、「一」 − 「１」 ＋ 「４」は「四」ではなく「二」になった。

　一方、「父」 − 「娘」 ＋ 「早苗」の答えとして、「岩瀬」を得た。早苗というのは、作品『黒蜥蜴』の登場人物、岩瀬庄兵衛の娘である。この事例では人物関係を見事に再現できたが、大抵はピントのずれた回答が戻ってくる。これは学習データの枠内での結果なので、偏りが出るのはやむを得ないところである。汎用性の高い結果を得るには、やはりそれなりの学習データ量が必要ということであろう。

　上記のコードをちょっと修正すると、指定した単語に類似していると判定された単語のリストを得ることができる（※具体的には、コードのword0類似度を調べたい単語を指定し、vec = param[word_indices[word0],:] とする。word1、word2、およびベクトルの足し算は不要なので削除する）。筆者は江戸川乱歩の著作を学習データに使用したので、「明智」で試したところ、以下の結果を得た。

順位	コサイン類似度	単語
第1候補	0.75769793602	？
第2候補	0.739668367405	早苗
第3候補	0.726747738227	……
第4候補	0.718360613538	夫人
第5候補	0.717179543556	岩瀬
表1　「明智」に類似すると評価された単語

　「小五郎」とか「探偵」とかを期待したのだが、一番類似した単語が「？」だというのは文字通り謎である。あとの人名は前述の、明智小五郎が活躍する探偵小説「黒蜥蜴」の登場人物である。

　そこで、「小五郎」で試してみた。以下がその結果である。

順位	コサイン類似度	単語
第1候補	0.725420430273	探偵
第2候補	0.691843578865	ゆうべ
第3候補	0.661063818008	エエ
第4候補	0.66042666185	明智
第5候補	0.659064832085	ホテル
表2　「小五郎」に類似すると評価された単語

　今度は、「探偵」とか「明智」とか、期待する単語が候補に現れた

Further Study

　冒頭に例示したMikolovの論文では、計算量を削減するため、出力ベクトルの個数を入力ごとにランダムに増減させている。また、計算量削減の手法として、ネガィテブサンプリングというものがよく用いられる。ネット上に実装例も見いだせるので、興味のある方は参考にされたい。

終わりに

　本稿では、word2vecの簡単な実装例を紹介した。word2vecは意味の近さによる単語の分類（正確には文章中の出現位置の類似性）が可能になるため、自然言語処理における広範囲の応用が期待できると言われている。大量の訓練データを必要とするところが大変であるが、実際にword2vecを使用するような局面で本稿がご参考になれば、幸いである。

「ディープラーニング習得、次の一歩」