Lesson 3 NumPyによる数学計算と、数学用語の「テンソル」:機械学習&ディープラーニング入門(データ構造編)
NumPyのデータ構造「多次元配列」を使って数学計算を行う方法を説明。また、そもそも機械学習やディープラーニングでは、なぜ数学計算が重要になっているのかについても言及する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
ご注意:本記事は、@IT/Deep Insider編集部(デジタルアドバンテージ社)が「deepinsider.jp」というサイトから、内容を改変することなく、そのまま「@IT」へと転載したものです。このため用字用語の統一ルールなどは@ITのそれとは一致しません。あらかじめご了承ください。
前回まで、AIプログラムで使うデータの構造に関して解説。基本的にはNumPyの多次元配列(ndarray)を使う、と説明した。今回は、そのndarray型のデータを使ってどのように計算するか、について説明しよう。※脚注や図、コードリストの番号は前回からの続き番号としている。
本稿で示すサンプルコードの実行環境については、Lesson 1を一読してほしい。
Lesson 1でも示したように、本連載のすべてのサンプルコードは、下記のリンク先で実行もしくは参照できる。
AIプログラムにおけるデータの計算
これからNumPyの具体的な使い方、つまり計算方法を説明するわけだが、その前に、「ディープラーニングにおける計算」について知っておくべきことがあるので、それから順を追って説明させてほしい。
AI・ディープラーニングで数学を使う理由
ディープラーニングの処理の中身は、さまざまな数式を使って、データの数値を幾重にも計算しながら変えていく処理、より直感的に表現するなら「数値をこねくり回すような処理」である。ディープラーニングの理論は数学を礎に築かれているわけで、その計算の大半を「NumPy」や「TensorFlow」のようなライブラリが肩代わりしてくれるとはいえ、その端々に、チラチラと数学の世界が垣間見えてしまうというのも現実である。
しかもその数学は、大学レベルと比較的高度である。このように高度な数学を用いる理由は、計算を楽にするためでもある。具体例を出してみよう。人の身長(height)の平均(average)を計算するなら、リスト7-1のようなコードになる。
hana_height, taro_height, jiro_height = 165.5, 177.2, 183.2 # Lesson 1のリスト2-1で宣言済み
average_height = (
hana_height +
taro_height +
jiro_height
) / 3
print(average_height) # 175.29999999999998
※先頭行は、タプルと呼ばれる構文を使って、複数の変数にまとめて値を代入している。
※Pythonの基本は1行1文であるが、カッコの中や+のような演算子の後は改行して文を継続できる。
難しいところはないだろう。(+算術演算子を使って)身長を足し合わせた数値を、(/算術演算子を使って)3人で割ることで、身長の平均値(average_heightオブジェクト)を算出している。
一見、こうやって計算すれば問題ないではないか、と思うかもしれないが、例えば3人ではなく、1000人や10万人ならどうだろうか? コードのボリューム(行数など)が333倍や3万倍とすごいことになってしまう。とても人間が書ける量ではなくなってくる。
そこで役立つのが、ここまでに説明してきたデータ構造とその処理体系(具体的にはNumPyやTensorFlowなどが提供する「多次元リスト」「多次元配列」「データフレーム」「テンソル」などと、その計算機能)なのである。ちなみに、Lesson 1のリスト2-1で示したリスト型のところでも同じ理屈で、データをまとめる必要性を説明した。つまり、NumPyなどのフレームワークを活用して、データを多次元配列構造にまとめることは、単にデータが扱いやすくなるだけでなく、計算も効率的に行えるようになるということだ。
試しに、上記のコードをNumPyの多次元配列を使って計算するコードに書き換えてみよう。
import numpy as np
array1d = np.array([ 165.5, 177.2, 183.2 ])
average_height = np.average(array1d)
average_height # 175.29999999999998
先ほどは(hana_height + taro_height + jiro_height) / 3と個別の値を使った計算式(=+や/などの演算子)が書かれていた部分が、np.average(array1d)というNumPyの関数に書き換わっている。このarray1dオブジェクトは、NumPyの1次元配列(多次元配列の一種)である。つまりリスト7-2は、多次元配列を使った計算式(=np.average()関数)に書き換えられているというわけだ。
繰り返しになるが重要なのでもう一度言うと、前掲のリスト7-1のような個別の値を使う場合だと、データの数が増えるほど、計算式部分のコードがどうしても長くなる。しかし、リスト7-2のような多次元配列を使う計算方法であれば長くならない。つまり多次元配列を使えば、計算式がシンプルで効率的になるのだ。
そもそも、数学の発想そのものが、このように複雑で面倒くさい計算を、シンプルで効率的な短い式で表現しようとすることである。そのため、ディープラーニングのような計算を効率的に行うには、やはり「数学」の利活用が非常に重要ということになるのである。
AI・ディープラーニングで使われる数学用語
このような理由から、データの計算では、数学が多用される。よって計算処理では、「個別の数値」や「多次元リスト」「多次元配列」のようなプログラミング用語ではなく、数学用語が用いられることが通例だ。具体的には、
- 「個別の数値」は、「スカラー」(scalar)
- 「1次元配列」は、「ベクトル」(vector)
- 「2次元配列」は、「行列」(matrix)
と呼ばれる。高校数学の授業で「スカラー」や「ベクトル」は聞いたことがあるのではないだろうか。
「行列」については、2012年度から高校数学で扱わなくなっているので、大学で学んでいない場合は知らないかもしれない。しかし難しいことはない。Lesson 1と2で学んだ多次元リスト(もしくは多次元配列)のうち、「2次元」のものが、「行列」である。行列の計算方法は、NumPyやTensorFlowに任せればよいので、とりあえず知らなくても大丈夫だ。
また、「3次元配列」以上の多次元配列に対応する数学は、大学で学ぶ。具体的には、
- 「多次元配列」は、「テンソル」(tensor)
と呼ばれる。「テンソル」は、TensorFlowのデータ構造の概念と同名である、と前回Lesson 2ですでに説明した。ここでようやく、
Pythonの「多次元リスト」 = NumPyの「多次元配列」 = TensorFlowの「テンソル」
と意味がつながる。つまりTensorFlowでは、データ構造に対して単に数学寄りの命名をしているというだけだ。単なる用語・名称の違いでしかないので、「テンソル……うわぁ、数学か……」と難しく考えすぎないようにしてほしい。場面場面によってこれらの用語は使い分けられるので、用語の違いは単純に記憶するしかない。
なおテンソルにも、プログラミング用語で言う「1次元・2次元・3次元……」といった「次元」(dimensions)対応する数学用語がある。それが「階」(ランク、階層)である。具体的には、
- 「個別の数値」は、「0階のテンソル」
- 「1次元配列」は、「1階のテンソル」
- 「2次元配列」は、「2階のテンソル」
- 「3次元配列」は、「3階のテンソル」
- 「N次元配列」は、「N階のテンソル」
のように表現する。
ここまで用語がたくさん登場したので、一覧表と図にまとめた。ぜひ、いま一度、頭の中を整理しておいてほしい。
| Python(多次元リスト) | NumPy(多次元配列) | TensorFlow/数学用語(テンソル) | 数学用語(値) |
|---|---|---|---|
| 個別の数値 | 0次元配列 | 0階のテンソル | スカラー |
| 1次元リスト | 1次元配列 | 1階のテンソル | ベクトル |
| 2次元リスト | 2次元配列 | 2階のテンソル | テンソル |
| 3次元リスト | 3次元配列 | 3階のテンソル | テンソル |
| N次元リスト | N次元配列 | N階のテンソル | テンソル |
| 表1 多次元配列に類する各種用語 | |||
数学とNumPyの関係が分かったので、NumPyの数学計算について簡単に機能を紹介しておこう。
NumPyの数学計算機能
前掲のリスト7-2ではnp.average(array1d)というコードで、npと名付けたnumpyモジュールのaverage()関数を呼び出していた。基本的にNumPyはこのように、関数の引数に多次元配列のndarrayオブジェクトを受け取り、計算結果を戻り値として返す。つまり、
<戻り値は計算結果> = <計算を行う関数名>(<多次元配列のデータ>)
という仕様になっている。
どのような数学系の関数があるかというと、代表的なものは以下のとおりだ。なお、これらすべての計算式を覚える必要はない。必要になった段階で、調べて使えばよい。
- 四則演算: 足し算:add()、引き算:subtract()、掛け算:multiply()、割り算:divide()、余り:mod()、※Python言語と同様に + - * / % も使える
- 丸め処理: 切り捨て:floor()、切り上げ:ceil()、四捨五入:round()
- 三角関数: サイン:sin()、コサイン:cos()、タンジェント:tan()
- 数学概念: 絶対値:absolute()、累乗:power()、平方根:sqrt()、指数:exp()、対数:log()
- 数学定数: 円周率π:pi、ネイピア数e:e、※これらは関数ではなく定数
- 統計処理: 合計:sum()、平均:average()、最小値:amin()、最大値:amax()、標準偏差:std()、分散:var()
数学の計算式は多種多様で、ここで取り上げたものはほんの一部である。詳しくは、NumPyの公式APIリファレンスの数学関数や統計関数を参照してほしい(※ただし、英語ページしかないので、日本語で読みたい場合はGoogle検索や翻訳などを活用して、必要な計算を探すしかない)。
NumPyを使った計算
これだけだと分からない部分も多いと思うので、NumPyによる数学計算の例をもう少し見ておこう。
まずは、3行2列の2次元配列を作成してみよう。リスト8-1は、その配列の形状(=shape)と次元数(=ndim)と要素*5数(=size)を出力している例だ。
array2d = np.array([ [ 165.5, 58.4 ],
[ 177.2, 67.8 ],
[ 183.2, 83.7 ] ])
print(array2d.shape) # (3, 2)
print(array2d.ndim) # 2
print(array2d.size) # 6
*5 プログラミングでは、配列内の個別の値は要素(element)と呼ぶが、数学の行列では成分(entry)とも呼ぶ。計算においては、数学に寄せて「成分」と記載している本も多いので注意してほしい。ちなみに、数学の行列は、大学数学では線形代数と呼ばれる分野に入る。
リスト8-2は、体重を90%にするダイエット目標を計算する例だ。数学や計算式の意味は本筋ではないので説明しないが、数学の行列の転置(T)や積(@:Python 3.5以降の場合。それ以前のPython 2系などの場合はmatmul関数)を使って計算している(※意味は分からなくてよい。ここでは行列計算が簡単にできることを知ってほしいだけだから)。
diet = np.array([ [ 1.0, 0.0 ],
[ 0.0, 0.9 ] ])
lose_weights = diet @ array2d.T
# Python 3.5以降の場合。それ以前のPython 2系などの場合は、以下のmatmul関数を使う必要がある
#lose_weights = np.matmul(diet, array2d.T)
print(lose_weights.T) # [[165.5 52.56]
# [177.2 61.02]
# [183.2 75.33]]
このような感じで行列計算できる。
もう一つ例を見ておこう。身長や体重の平均値を2次元配列(=行列)の状態で計算してみよう。
前掲のリスト7-2では、np.average(array1d)というコードで1次元配列(=ベクトル)の平均値を算出したが、このaverage()関数を2次元配列(=行列)に対して使うと、全要素(=全成分)の平均値を算出してしまう。
averages = np.average(array2d)
averages # 122.63333333333334
こうではなく、2次元配列データ内の身長および体重のみの平均値を出すには、NumPyの軸(axes:複数形。単数形はaxis)という概念を理解しておく必要がある(図9-1)。といっても難しくはない。
座標軸のような感じである。まず行と列を持つ2次元配列データであれば、行方向が軸「0」、列方向が軸「1」である。なお、軸番号は0スタートである。
average()関数のaxis引数(※デフォルト引数のため先ほどは省略されていた)に対して、この軸番号を指定すると、身長/体重別に平均値が計算できる。リスト8-4ではキーワード引数の形で軸「0」を指定している。これにより、行方向に身長と体重の平均値が計算される。
averages = np.average(array2d, axis=0)
averages # array([175.3 , 69.96666667])
ちなみに3次元になると、[]が一番外側になる奥行き方向が軸「0」で、行方向が軸「1」、列方向が軸「2」と変わるので注意が必要だ(図9-2)。
3次元配列で行方向に平均値を計算するのであれば、軸「1」を指定すればよいので、例えばリスト8-5のようになる。
array3d = np.array(
[ [ [ 165.5, 58.4 ], [ 177.2, 67.8 ], [ 183.2, 83.7 ] ],
[ [ 155.5, 48.4 ], [ 167.2, 57.8 ], [ 173.2, 73.7 ] ],
[ [ 145.5, 38.4 ], [ 157.2, 47.8 ], [ 163.2, 63.7 ] ] ]
)
avr3d = np.average(array3d, axis=1)
print(avr3d) # [[175.3 69.96666667]
# [165.3 59.96666667]
# [155.3 49.96666667]]
行と列を持つ表データが出てくると、図9-1や図9-2のイメージで示したような空間を把握する能力が要求され始めるので、「頭が混乱する」と感じる人もいるかもしれない。これはデータを扱うかぎり仕方がない部分でもあり、作業数をこなして慣れていくしかないだろう。慣れてしまえば最初ほど混乱しなくなるものである。
NumPyについてはこれぐらいにしておこう。図9-3に示すような、多次元配列データへのアクセス方法やデータのフィルタリングなども学んでおいた方がよいが、これらについては実際のデータを扱う連載『初めてのニューラルネットワーク&ディープラーニング実装(TensorFlow 2+Keras(tf.keras)入門)』の中であらためて説明する。
 図9-3 多次元配列データへのアクセスとフィルタリングの例(TensorFlow公式チュートリアルより引用)
図9-3 多次元配列データへのアクセスとフィルタリングの例(TensorFlow公式チュートリアルより引用) 配列のインデックス番号は0スタートとなる。範囲指定方法は、<開始インデックス番号>:<終了インデックス番号>という仕様で、<開始インデックス番号>を省略すると「先頭から」となり、<終了インデックス番号>を省略すると「末尾まで」となる。
[:10000]とすると、「先頭から<終了インデックス番号=10000>まで」の範囲でデータが抽出される。<終了インデックス番号>の要素自体は、抽出範囲に含まれない仕様になっていることに注意が必要だ。よって、インデックス番号が0〜9999の10000件分のデータが抽出されることになる。
[10000:]とした場合は、「<開始インデックス番号=10000>から末尾まで」の範囲でデータが抽出される。具体的には、インデックス番号が10000〜末尾のデータ(件数はデータの長さによって違う)が抽出されることになる。0スタートではなく、最初を1件目と数えるなら、10001件目〜末尾までとなる。
以上、AIのデータ構造「多次元配列」を使った計算方法について説明した。次回はまとめとして、これまでの3回分のLessonのポイントを、箇条書きで短く再確認する。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ



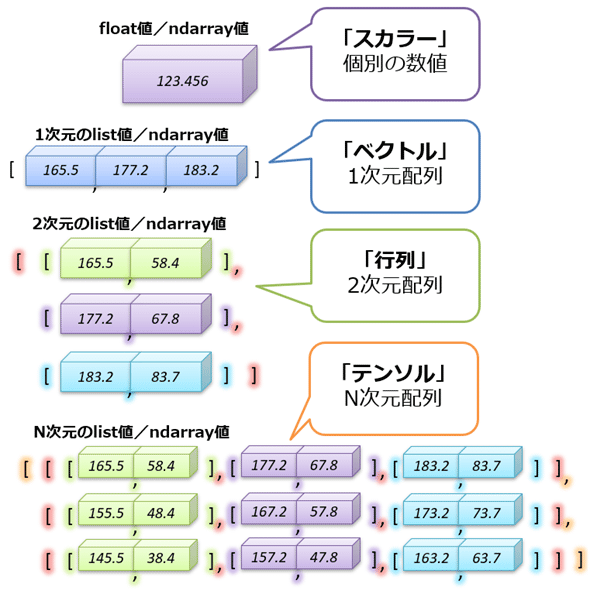
 図9-1 NumPyの軸の概念図(2次元配列)
図9-1 NumPyの軸の概念図(2次元配列)  図9-2 NumPyの軸の概念図(3次元配列)
図9-2 NumPyの軸の概念図(3次元配列) 



