機械学習の精度を左右する「データ加工」の基礎知識――「欠損値」への対処に見る「守りのデータ加工」編:「AI」エンジニアになるための「基礎数学」再入門(4)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回から2回に分けて「データ加工」の手法を紹介します。まずは「守りのデータ加工」です。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。初回は、「AIエンジニア」になるために数学を学び直す意義や心構え、連載で学ぶ範囲についてお話ししました。
また第2回では、データの種類を紹介しました。そこでは、数値としてのデータ自体、あるいはその統計量には尺度によって意味のあるもの(=情報として価値があるもの)と、そうでないものがあることを確認しました。忘れてしまった方は、もう一度目を通していただくことをお勧めします。第3回では、統計について、その概念と各種統計量(「最頻値」「中央値」「平均値」「分散」など)が表す意味について学びました。そこでは、「統計量は数値として抜き出された情報である」ということを述べました。
「データ加工」は分析者にとって腕の見せどころの一つ
ここから発展的に考えてみると、「どのようにすると、より多くの情報、そしてより価値のある情報を抜き出すことができるのか?」という疑問が湧いてきませんか? 今回、そして次回の内容である、「データ加工」はまさしく、その疑問を解消するものになっています。それに加え、データ加工は分析者にとって腕の見せどころの一つです。
例として、「データと機械学習を用いることで値を予測し、その予測精度を競う」ような状況があったとします。機械学習のアルゴリズムは多くの人がディープラーニングや勾配ブースティングといった流行していて実績のあるアルゴリズムを使用することでしょう。すると、設定によって多少は上下するものの、同じデータを使っていれば基本的に皆の精度は似たり寄ったりになります。この場合、勝負の命運を分けるのは「予測に用いるデータの量と質」です。すなわち、より多く、より価値のある情報を用意したものが勝つということです。
データ加工は知識、スキル的にも基本中の基本の領域なので、地味、泥臭いなどといったイメージを持たれがちです。しかし、先ほど説明したように、非常に重要な領域なので、いい加減にせずしっかりと学んでいきましょう。
「欠損値」への対処
「欠損値」とはその名の通り、値が入っていない要素のことを指します。例として、図1を見ると、「体脂肪」列の最終行にあるもので本来は値は存在しませんが、データの表示方式によって「NaN」「null」「NULL」などと表示されていることもあります。
このような欠損値が発生する原因は大まかに3つあります。
- 偶然
- 他の値の影響
- 元の値(あるいはデータとして保持していないもの)の影響
欠損値が生じた原因は、データを生成した担当者に問い合わせる。あるいは、欠損値の場合と値が存在する場合とで他の列の平均値などを算出し比較することで特定できます。
欠損値は、そのまま放っておくとプログラムがエラーを起こしたりする原因となります。よって、欠損値が存在する行を削除するか、欠損箇所に仮の値を埋めるなど対処する必要があります。
ただし、万能な対処法はありません。それはデータの行数や欠損値の発生頻度によって最適な対処方法が変わるからです。あくまで目安的なものになりますが、発生原因別の一般的な対処法を確認していきましょう。
【1】欠損値が偶然生じている場合
欠損値が偶然発生するとは、どのようなケースが考えられるでしょうか。例えば、計測器の故障や、記入し忘れなどによって発生する場合などがそれに当たります。
これについては、「やむなし」といったところです。基本的には再現が難しいので、次のように対処しましょう。
欠損値が存在する行を削除する
こちらは単純です。「使えないのならば消してしまえ」という意識からの対処です。おおむね、欠損値の出現頻度がデータの行数に対して小さければこの対処で差し支えないでしょう。
しかし、そうではない場合もあります。例えば、データ数が非常に少なく、欠損行を削除する前後で他の値の平均値や分散が大きく変化する場合などがあります。こういった場合は次のような対処を試してみましょう。
代表値で埋める
こちらも意識は単純です。「当たり障りのない値を代入しておこう」というものです。前回紹介した統計量が使われます。
質的データの場合は最頻値で埋め、量的データの場合は、平均値か中央値で埋めるのが一般的です。どちらで埋めるか迷ってしまいますが、ここにも残念ながら普遍的な解はありません。基本的には平均値ですが、特殊な「分布」(分布については後の「確率分布」の回で解説します)となったデータについては中央値を代入するケースもあります。
【2】他の値の影響で欠損値が発生している場合
これは、例えば「体重が重かったことで、体脂肪率を計ることを恥じてしまった被計測者が計測を拒否した」ケースなどが該当するでしょう。
少し高度な領域になりますが、このような場合には次のような対処が存在します。
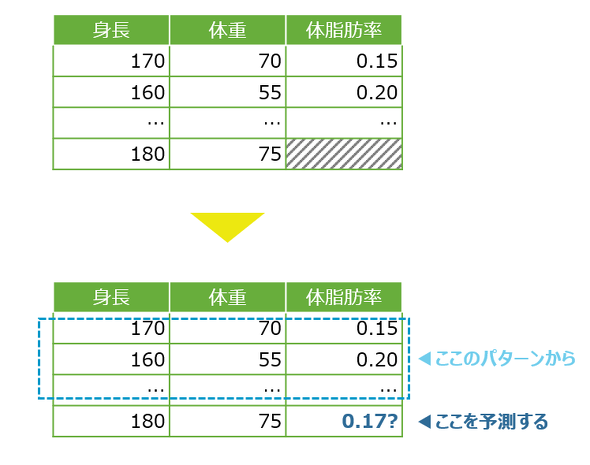
他の値からの予測値で埋める
ここで、身長、体重と体脂肪率は相関関係があるという前提に立ってみれば、非欠損行から見られる体重と体脂肪率の相関の様子から、欠損行の体脂肪率を推測できることになります。
この具体的な手法は後の「機械学習」の回で解説しますので、今はイメージだけつかんでおいてください。
【3】元の値(あるいはデータとして保持していないもの)の影響で欠損値が発生している場合
これが一番困ったパターンです。なぜなら、先ほどとは違い、他の値から再現できないからです。具体例としては、「体重は普通にもかかわらず、体脂肪率を計ってみたところ思いの外、値が高く、それを恥じてしまった被計測者が申告を拒否した」ケースなどがこれに当たるでしょう。
基本的には「なすすべなし」といったところですが、質的データかつ欠損値の元の値がほとんど同じだと考えられる場合は次のような対処が存在します。
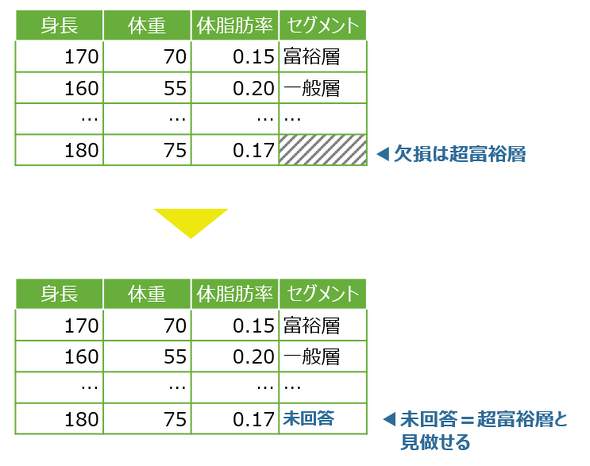
そのまま欠損値として扱う
ここに、自己申告で記録される資産額セグメント(超富裕層、富裕層……といった値)が付与されたデータがあった場合に、欠損値の元の値(=本来の値)のほとんどが超富裕層だったとします(「超富裕層は謙虚な人が多い」「秘密主義の人が多い」といった適当な想定でもしておいてください)。
この場合、欠損値に「未回答」「欠損」などといった文字列を代入しておけば、実質的にその値=超富裕層ということが表現できます。実行の見極めが難しい対処ではありますが、頭の片隅に置いていても損はないはずです。
次回は、「攻めのデータ加工」
以上が原因別の欠損値に対する一般的な対処法でした。これらは、大まかに分けると「異常なデータを除外する」あるいは「除外はもったいないのでなるべく情報量をキープするといった意識に起因する」もの、すなわち「守りのデータ加工」でした。
次回は、「Rounding(丸めこみ)」「Binning(区分け)」「log(対数)変換」「root(平方根)変換」「pow(べき)変換」など、数学を駆使して「いかにデータを増やすか、いかに質を高めるか」という「攻めのデータ加工」を紹介します。
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。![[Python入門]Pythonってどんな言語なの?](https://image.itmedia.co.jp/ait/articles/1904/02/news024.gif) [Python入門]Pythonってどんな言語なの?
[Python入門]Pythonってどんな言語なの?
機械学習に取り組んでみたいという人に(そうでない人にも)向けて、Pythonプログラミングを基礎からやさしく解説する連載をPython 3.10に合わせて改訂します。 Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。初回は、筆者が実業務で有用としているライブラリ/ツールを7つ紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

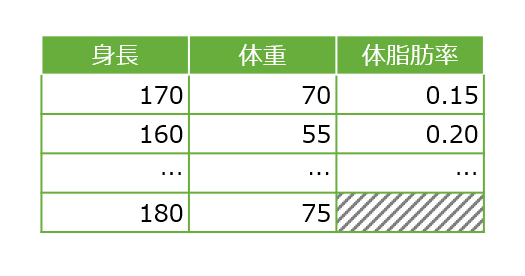 図1 欠損値のあるデータのイメージ
図1 欠損値のあるデータのイメージ