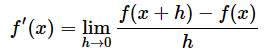［AI・機械学習の数学］微分法の基本を身につけて「変化」を見極めよう：AI・機械学習の数学入門（2/3 ページ）

[羽山博，著]

目標【その3】： いよいよ微分のお話（導関数を理解する）

　さて、いよいよ微分のお話です。平均変化率の式で、間隔hをどんどん小さくしていくと接線の傾きが求められます。微分とは、その「接線の傾き」を表す式を求めることとも考えられます（厳密な定義ではありませんが、最初はそういうイメージで十分です）。まずは以下の式を見てください。

　このf'(x)は、「関数f(x)の導関数（どうかんすう）」と呼ばれます。微分とは導関数を求めることに他なりません。つまり、この式が微分の定義です。

　ここでの目標は、導関数を表す式（つまり上記の式における右辺）の意味を理解することです。

解説：微分の考え方と書き方について

　いきなりものすごい式が出てきてハードルが急に上がったように思った人がいるかもしれませんが、右辺の式に見覚えはないでしょうか。右端の部分は平均変化率の式そのものでよね。つまり、平均変化率をどうこうしてやれば、微分ができるということです。

　ここで、新しく出てきた記号の読み方をまず確認しておきましょう。新しく出てきたのは、左辺のf'(x)と右辺のlimの2つだけです。

　左辺の'は「プライム」と読みます。従って、f'(x)は「エフプライムエックス」や「エフプライムかっこエックス（かっことじ）」のように読みます（※「エフダッシュ」ではありません）。

　右辺のlimは「リミット」と読みます。ある変数の値を何らかの値に限りなく近づけていく、といった意味なのですが、これが理解できれば微分も理解できるので、ここから詳しく見ていくことにしましょう。

　というわけで、ここから平均変化率がどう微分に結び付いてくるのかというお話をします。最終的には、超カンタンな計算方法にたどり着くのですが、考え方が大事なのでゆっくりと読み進めてください。

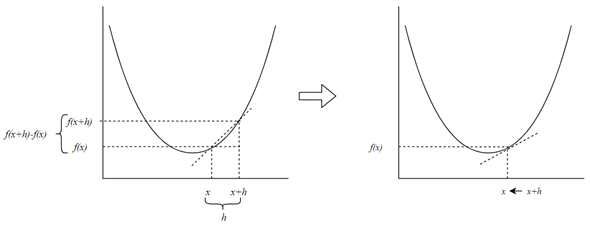
　平均変化率は図6の左に示した「斜めの点線の傾き」のことでしたね。このような状態から、間隔hをどんどん小さくしていくと、いったいどうなるでしょうか。

図6　接線の傾き

　直感的に分かると思いますが、図6の右のように接線の傾きに近づいていきます（念のため、この動きを追いかけた動画も用意しておきます）。

動画1　接線の傾き

　平均変化率の「間隔」が限りなく0に近づいていくので、接線の傾きは「ある瞬間の変化率」とも表現できますね。

　そこで、接線の傾きを求めるために、平均変化率の式で、間隔hをどんどん小さくしていき、限りなく0に近づけてみましょう。そのときに、平均変化率がどのような値に近づくかを求めるといいですね。