[AI・機械学習の数学]微分法の基本を身につけて「変化」を見極めよう:AI・機械学習の数学入門(1/3 ページ)
式の値が最小になるときのxの値を求めたり、値がどのように変化していくかを見たりするためには微分が活用できる(回帰分析・重回帰分析につながる基礎知識)。今回は平均変化率から始め、微分の基本を一歩ずつゆっくりと追いかける。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
機械学習では、値を少しずつ変えていき適切な値に近づけていくという計算をよく行います。最初は適切な値とは大きく離れていますが、徐々に近づいていくでしょうから、変化率を見れば適切な値に近づいているかどうかが分かります。変化率が無視できるほど小さくなれば、そのときの値が最適な値と見なせるはずです。
ところで、そもそも変化率というのはどういうものでしょうか。今回は変化率の意味を確認し、さらに微分の考え方と計算方法を学びます。
目標【その1】: 平均変化率を理解する
平均変化率とは、一定の間隔の中でどれだけ値が変わったか、ということです。
で表されます。平均変化率が正なら増えていることを表し、0なら変化していないことを表します。負なら減っているということが分かります。また、ある時点での平均変化率よりも次の時点の平均変化率が大きければ、ますます増加する傾向にある、ということも分かります。
解説:平均変化率の意味と利用例を知る
目標のところでは簡単な式を記しただけですが、平均変化率はさまざまな場面で使われます。例えば、車が3時間で240km進んだとか、株価が6か月で300円上がったとか、日常の例を挙げればキリがありません。最近(2020年5月現在)の深刻な話題としては新型コロナウィルスの感染者が1日でどれだけ増えたか、といったことも平均変化率と考えられます。平均変化率が大きくなると拡大の傾向にあり、小さくなると収束に向かっているということも分かります。
平均変化率は単なる割り算で求められます。実際のところ、車の例なら途中でサービスエリアに寄ったりすることもあるでしょうし、株価は秒刻みで上下するので、「間隔」の取り方によって変化率は変わりますが、「ならして」みるとこうなるという意味で「平均変化率」と呼びます*1。
*1 ちなみに、この場合の「ならして」は「均して」と書きます。
繰り返しになりますが、平均変化率は、変化した値を、時間や期間などの間隔で割れば求められることが分かります(km/hなどの単位は省略してあります)。以下の図で見てみましょう。100kmの地点から340kmの地点まで移動するのに、1時から4時まで時間がかかっています。
この場合、時間は4−1=3で、距離は340−100=240なので、平均変化率は、
になるわけです。平均変化率は、図中の斜めの点線の傾きに当たることも分かりますね。当然のことながら、間隔が異なると平均変化率が変わることもあります。
この場合、時間は3−1=2で、距離は220−100=120なので、平均変化率は、
となります。平均変化率の計算は単なる引き算と割り算ですね。では、練習問題として、もう少し抽象化した例にチャレンジしてみましょう。
練習問題
前回は距離の二乗和の最小値を求めるために二次式を使いました。二次式は中学・高校で慣れ親しんでいるので、ここでも簡単な二次式(二次関数)を例に平均変化率を計算してみましょう。以下のグラフは、
のグラフです*2。
*2 ボールなどを投げ上げたときの時間tと位置yの関係もy=−1/2gt2+atという二次式で表されます(gは重力加速度と呼ばれ、地球上では約9.81です。aは初速です。なお、投げ上げたボールは下に落ちてくるので、下の図とは反対の上に凸なグラフになります)。
xの値が1.5から2まで変わるときのyの値の変化率を求めてみましょう。つまり、図中の斜めの点線の傾きを求めます。図中のbの長さをaの長さで割ればいいですね。aの長さは、xの値の1.5と2から求められます。これはカンタン、2−1.5=0.5です。一方、bの長さを求めるためには、1.5や2に対応するyの値を求めておく必要があります。
では、xが1.5のとき、yの値はいくらになるでしょうか。これは、(1)式のxに1.5を代入すれば求められます。以下の穴埋めをしてみましょう。計算が必要な箇所は電卓を使っちゃいましょう。答えは、オレンジ色の部分をクリックまたはタップすると表示されます。
x = 1.5のとき、
y = 3 ⋅ 1.5 2 - 5 ⋅ 1.5 + 1
= 0.25
1.52=2.25なので、y = 3 ⋅ 2.25 − 6 ⋅ 1.5 + 1を計算すればいい、ということが分かりますね。答えは0.25でした。
同様にして、
x=2のとき、
y=3 ⋅ 2 2 − 5 ⋅ 2 + 1
= 3
という値も得られます。
いったん整理しておきましょう。
です。これで平均変化率が求められますね。ここも穴埋めでいきましょう。
3 - 0.25
平均変化率 = ─────────
2 - 1.5
= 5.5
はい、平均変化率が求められました。この5.5という値はxが1増えるとyは5.5増えるという意味です。
目標【その2】: 平均変化率を文字式で表してみる
xの値に対して、何らかのルールでyの値が対応する、ということを、
と表してみることにします。このとき、xがhだけ増えたときの平均変化率は以下の式で表されます。
解説:平均変化率を文字式で表してみる
平均変化率を文字式で表すに当たって、ちょっと前置きのお話をしておきましょう。目標に示した「xの値に対して、何らかのルールでyの値が対応する」というのは、要するに図3(下に再掲)のようなグラフが書けるということです。
そのルールを「f」という文字で表し、「f」というルールにxを与えるということを、
と表してみましょう。すると、yの値が決まるので、
となります。前掲の図3の例なら、
です。なんだか回りくどい言い方をしているようですが、このように、あるルールに従って値が対応することやそのルールを表す式のことを「関数」と呼びます。ルール(関数)が複数あるときにはgという文字を使うこともあります。f(x)やg(x)というように区別して表すわけです。回りくどさついでに、別の図で「関数」を表しておきましょう。
この図はxの値がyの値に対応することを表しています。fというのが対応を表すルール(関数)ですね。図からも読み取れますが、異なるxの値に対して、yの値が同じになることもあります。図3(二次式のグラフ、下に再掲)の例でいえば、x=0のときにも、x=5/3のときにもyの値が1になります。
先ほど見た二次関数 y=3x2−5x+1では、係数は3や5といった具体的な数値でしたが、これを一般的に表すために文字で表してみましょう。次のような感じですね。
ここで注意すべき点は、a,b,cはいずれも定数であるということです。一方、y,xは変数です。a,b,cは何か分からないけれども決まった値であり、y,xはさまざまな値を取るということですね。慣れれば特に意識しなくても分かりますが、どれが定数でどれが変数なのかをちょっと意識しておくと式の意味合いや取り扱いの方法がよく分かり、見通しがよくなります。
では、「ルールfによってxの値がyの値に対応していますよ」ということが分かるように、yの代わりにf(x)を使って書いてみてください。答えは、オレンジ色の部分をクリックまたはタップすると表示されます。
f(x) = ax2 + bx + c
カンタンでしたね。xとyだけだと「xとyに関係がある」ということが伝わりませんが、xとf(x)なら、「xに何かのルールを適用したものがf(x)である」という関係がよく分かります。この方が、関数というコトバのイメージに合っていますね。こういう書き方、ちょっとカッコイイですし。
続いて、平均変化率です。実は、 ax2+bx+cに限らず、どんな関数でも同じことなので、ここからはもうf(x)だけで話を進めます。
xの値がhだけ増えたとします。このときの平均変化率を求めてみましょう。
というわけですから、平均変化率は以下の式になります。
この式と図5をじっくりと見て、式と図の対応関係を確認しておいてください。次の「微分のお話」で使うためです。
これで、平均変化率が一般的に表せました。上でも述べましたが、どんな関数でも同じです。
次のページは……
次のページで「いよいよ微分のお話」に入ります。
- 目標【その3】: いよいよ微分のお話(導関数を理解する)
- 目標【その4】: 微分の計算方法(導関数の求め方)
Copyright© Digital Advantage Corp. All Rights Reserved.

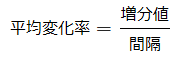


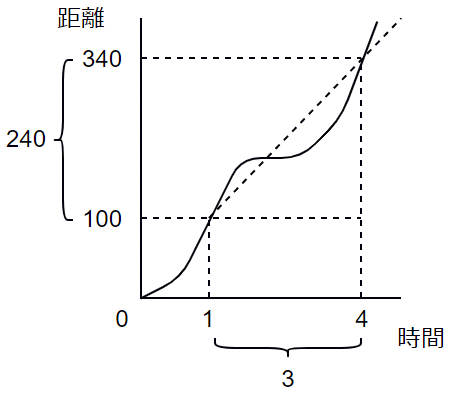 図1 平均変化率を求める
図1 平均変化率を求める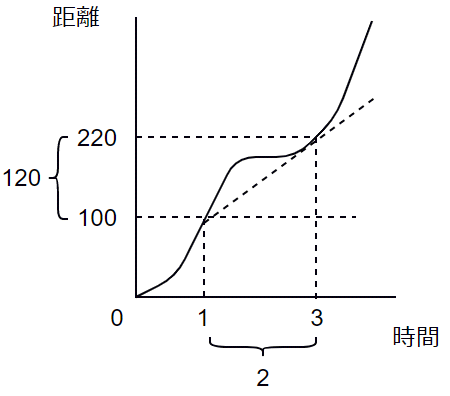 図2 間隔が異なると平均変化率も変わる
図2 間隔が異なると平均変化率も変わる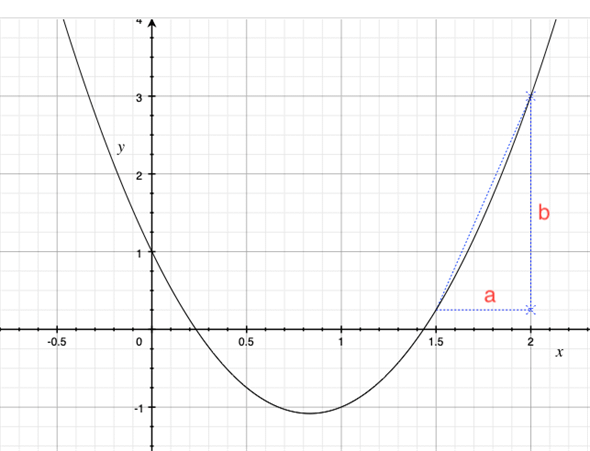

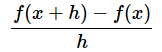
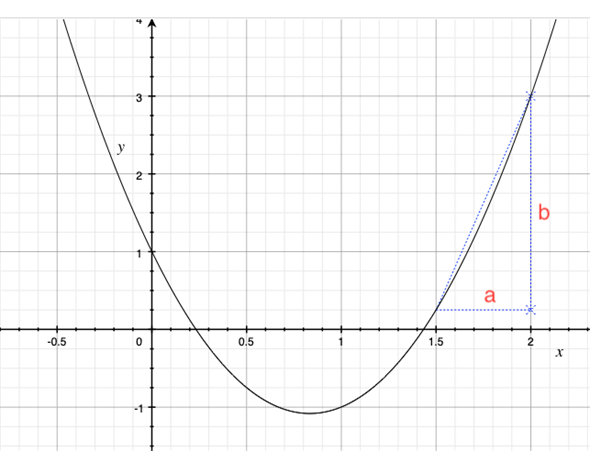
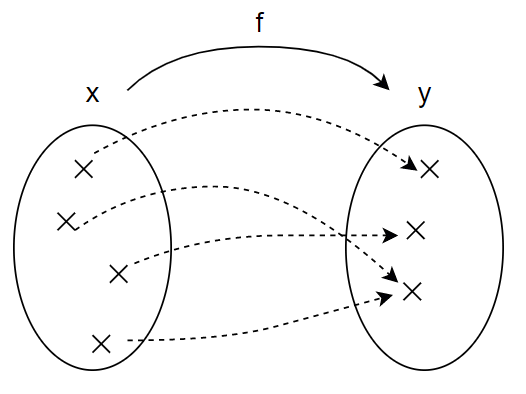 図4 関数とは値の対応のこと
図4 関数とは値の対応のこと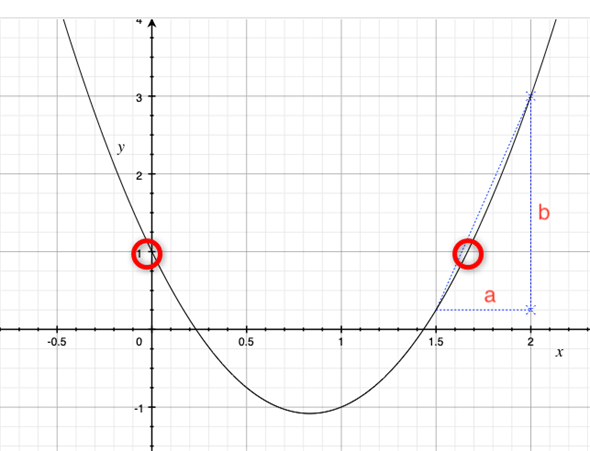
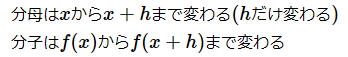
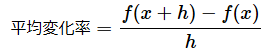
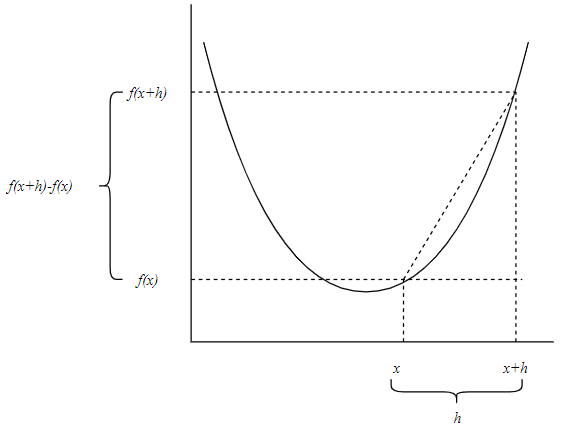 図5 平均変化率を一般的に表す
図5 平均変化率を一般的に表す



