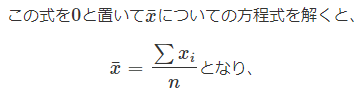[AI・機械学習の数学]微分法の基本を身につけて「変化」を見極めよう:AI・機械学習の数学入門(3/3 ページ)
練習問題
以下の関数を微分してみましょう。
(1) f(x) = 7x3をxで微分する
(2) f(x) = 10をxで微分する
(3) f(x) = 2x4+3x2+5をxで微分する
(4) f(t) = t2−4t+4をtで微分する
解答
(1) f'(x) = 21x2
(2) f'(x) = 0
(3) f'(x) = 8x3 + 6x
(4) f'(t) = 2t−4
(1)は、指数が3なのでそれを係数に掛けて、7 × 3=21が導関数の係数になりますね。指数の方は1つ減らすと2です。よって、21x2となります。
(2)は、ちょっとひっかけっぽいですが、定数項しかないので、0になります。f(x)の値は常に10なので、全く変化しませんね。だから変化率は0です。
(3)は、手順通り各項を計算していけば求められます。
(4)は変数としてtを使っただけです。やはり手順は同じです。
解説(続き):微分の定義と計算方法について
微分の意味や定義も分かった、計算方法も分かった、めでたしめでたし……と言いたいところですが、「いや、ちょっと待ってくれ」と思った人はいないでしょうか。微分の定義は以下のようなものでした。
そして、計算方法は以下のようなものでした。
のとき、
これでは、定義と計算方法がどうつながっているのかが分かりませんね。意味もやり方も分かったから、なんだか分からない面倒な途中の話はいいや、と投げ出さずに、上の定義と下の計算方法がつながっている(=導き出せる)ことを確認してみましょう。ただし、厳密に証明するとかなり長くなるので、簡単な例で答えが合っていることだけを確かめるにとどめます。
では、例として、f(x)=ax2を取りあげます。この導関数を微分の定義に当てはめて計算してみましょう。簡単な例とはいえ、式の変形が少し細かくなるので動画も用意しておきました。
動画3 導関数を求める(二次関数の例)
まず、微分の定義に、関数の式を代入してみましょう。
[A] ⋯
これが導関数の定義
[B] ⋯
f(x+h)=a(x+h)2とf(x)=ax2を代入した
次に、分子の式を展開して、整理してみます。
[A] ⋯
二乗の展開の公式を使って式を展開した
[B] ⋯
分配法則を使ってカッコを外した
[C] ⋯
ax2と−ax2の計算をした(0になるのでこの項が消える)
[D] ⋯
hで約分した
ax2と−ax2が出てくるので、この項が消えてくれます。式を変形しているときに、こういうふうにきれいに消えてくれるのはうれしいですね。
0で割り算することは禁止されていますが、hは0ではなく、0に限りなく近い値なので約分ができます。また、
と定義されており、
で、さらに、多項式の場合は各項に分けて計算できるので、結局のところ、上の式は以下のようになります。
2axの項はhの値が変わっても2axのままですね。定義通りに計算していくと、
となりました。一方、目標【その4】では、
という簡単な計算方法だけを示しましたが、この式のnに2を当てはめてみると、
となり、上で計算した結果と同じになっていることが分かります。というわけで、目標【その4】で見た計算方法は、ちゃんと微分の定義から導き出せるようだ、ということが分かりました(「ようだ」と言葉を濁したのは、これがちゃんとした証明になっておらず、(ax2)'の場合には答えが合っていることを確認しただけだからです)*6。
では、最後に少しだけ応用的な例題でおさらいをして終わりにしましょう。といっても、同じような式ばかりではつまらないので、これまでに学んだΣにも登場してもらいましょう。
を、
してみてください。
「なんじゃこりゃあ」と思った人もいるかもしれませんが、
に注目すれば、手順通りに計算できます(図10)。Σが含まれていますが、それらは単なる係数(定数)にすぎません。
従って、答えは、
となります。ちなみに、
平均を求める式が導き出せます。
さて、ずいぶんといろんなお話をしてきましたが、微分の計算そのものはとても簡単だということが分かったと思います。とはいえ、単に計算ができるのと、意味をちゃんと理解しているのは大違いです。平均変化率のお話から微分の定義を学び、それを基にいくつかの例で導関数を求めたことにより、微分の意味がよく分かった(思い出せた)と思います。
実際には、関数が分かっていても、導関数が簡単には求められない(ここで示した簡単な計算方法だけでは微分できない)関数や方程式もあります。そのような関数を取り扱うためには、コンピュータシミュレーションによって数値計算をすることがあります。その場合、定義に戻ってhの値を少しずつ変えていくことにより、近似値を求めたりします。そういうわけで、微分の定義が役に立つ日がいずれやって来ることと思います。
次回は……
今回は微分の考え方と基本的な計算の方法について説明しました。毎回、基本のお話に加えて、いくつかの公式と機械学習につながる応用例についても触れているのですが、今回は学ぶべきことが多く、やや複雑なところもあったので、微分に関するいくつかの公式と、応用例は次回に譲ることとします。
Copyright© Digital Advantage Corp. All Rights Reserved.

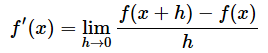
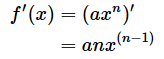
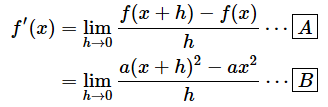
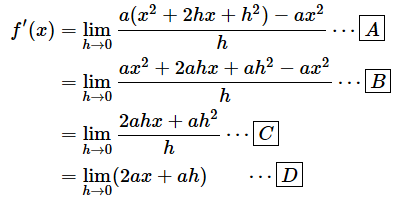
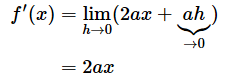


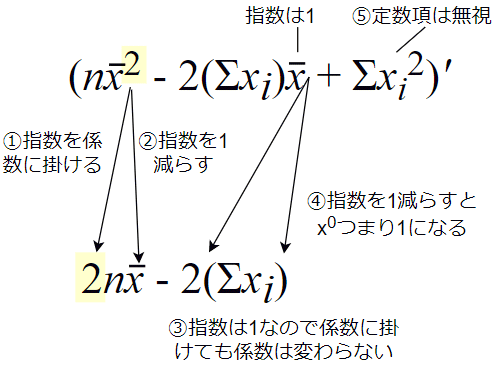 図10 Σを係数に含む関数を微分する
図10 Σを係数に含む関数を微分する