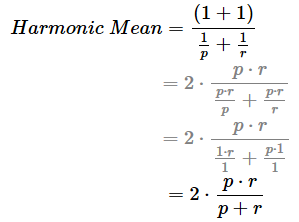［評価指標］F値（F-measure、F-score）／F1スコア（F1-score）とは？：AI・機械学習の用語辞典

用語「F値」、別名：「F1スコア」について説明。二値分類タスク（問題）に対する評価指標の一つで、適合率と再現率のトレードオフ関係に着目し、2つの値を調和平均「2×（適合率×再現率）÷（適合率＋再現率）」した値を指す。

» 2023年11月06日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

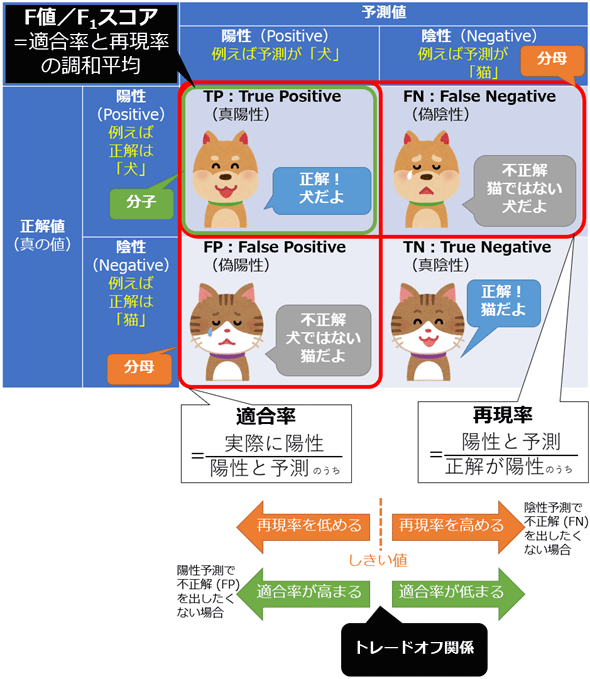
　統計学／機械学習におけるF値（F-measure）もしくはFスコア（F-score）とは、（基本的に）二値分類のタスク（問題）に対する評価指標の一つで、適合率（Precision）と再現率（Recall）のトレードオフ関係に着目し、2つの値を調和平均（詳細後述）した値のことである（図1）。0.0（＝0％）～1.0（＝100％）の範囲の値になり、1.0に近づくほどより良い。1.0に近いことは、適合率と再現率の両方が同時にできるだけ高いことを意味するので、「最も効率よくバランスの取れた機械学習モデル」と言える。

　F値の計算は、2×適合率×再現率を適合率＋再現率で割ることで計算できる。

図1　「F値」のイメージ

　調和平均（Harmonic Mean）とは、平均を計算する手法の一つで、“率”の平均（＝2つの値の比、つまり分子／分母で構成された指標において、その分子を基準とする場合の平均）を算出するのに適している。ちなみに通常の算術平均は、“量”の平均を算出するのに適している。また調和平均には「要素間のバランスを重視する」という特徴がある（参考：「平均の意味と正確な計算方法に関する浅見 : 調和平均の例解を中心に」）。

　例えば距離40kmと距離60kmという「2つの移動距離（km）」のような“量”に対しては算術平均を行い平均距離50kmと計算するが、時速40kmと時速60kmという「2つの移動時速（km/h）」のような“率”（＝距離／時間で構成された指標において、その分子である距離を基準とする場合）に対しては調和平均を行い平均時速48kmと計算する（計算方法は後述）。

　例えばpとrという2つの“率”の調和平均を算出する式は以下のようになる。

　この数式を使うことで、先ほど例に出した平均時速48kmは求まる（2×（40×60）／（40＋60）＝2×（2400）／（100）＝48）。

　F値の場合は、適合“率”と再現“率”のバランスを重視した平均を算出するため、算術平均ではなく調和平均を用いる。

　調和平均の計算式におけるpをPrecision（適合率）、rをRecall（再現率）と置くと、下記の計算式になる。TP／FP／FNの意味は、図1や混同行列の用語解説を参考にしてほしい。

　この基本的な調和平均による計算値は、F₁スコア（F₁-score）と呼ばれる。

　適合率は「陽性の予測がより正確になっていること（＝陽性予測においては、できるだけ不正解を出したくないこと）」を重視する。一方の再現率は「陽性の予測での取りこぼしをできるだけ少なくしたいこと（＝予測時に「陰性」と間違う不正解はできるだけ出したくないこと＝陰性予測においては、できるだけ不正解は出したくないこと）」を重視する。

　F値は、トレードオフ関係にある適合率と再現率でバランスを取りたい場面で使いやすい評価指標である。例えばあなたがお医者さんで「受診者の病気を発見したい」とする。そこで「病気かどうか」という二値分類を予測する機械学習モデルを作成したとする。

　例えば健康診断では病気である人を見逃したくないため、再現率が重要である（＝「陰性予測においては、できるだけ不正解『FN』は出したくない」ということ）。

　例えば精密検査では病気でない人を誤診したくないため、適合率が重要である（＝「陽性予測においては、できるだけ不正解『FP』は出したくない」ということ）。

　「今回は健康診断でも精密検査でもなく、これらの両者のバランスが最もよくなるように（＝調和平均値が1.0に近くなるように）診断したい」という場合に、F値を評価指標／評価関数として用いればよいというわけである。

　ここまでF₁スコアという最もベーシックなF値を説明してきたが、より柔軟なF値を計算するためのバージョン（具体的には重み付きF値／F_βスコア）もあるので、こちらの記事で紹介している。

　また、F₁スコアを活用する多クラス分類向けの評価指標に、macro-F₁（マクロ平均F₁）スコアやmicro-F₁（マイクロ平均F₁）スコアもあるので、こちらの記事で紹介している。