フリーペーパーの「配送計画問題」に見る、「局所探索法」の基本的な考え方：リクルート事例で分かる数理最適化入門（4）

リクルートにおける数理最適化の応用事例を通じて、数理最適化とは何か、どのようにビジネスに応用できるのかを紹介する連載。今回は、フリーペーパーの「配送計画問題」をどう解決したかを解説する。

[濱田賢吾, 棚橋耕太郎，リクルート]

　本連載「リクルート事例で分かる数理最適化入門」では、リクルートでの数理最適化の応用事例を通して、数理最適化がどのようにビジネスに応用できるのかを紹介します。連載第4回の本記事では、前回に引き続き、リクルート各サービスにおける数理最適化の応用事例を紹介します。

　今回は、「フリーペーパーの配送計画の策定」の事例を紹介します。この事例では、「扱う問題が汎用（はんよう）の数理最適化ソルバーが苦手とするタイプの問題である」という難しさがありました。

　前回までで紹介した事例では、汎用の数理最適化ソルバーを用いた求解を行いましたが、全ての問題が汎用ソルバーで効率的に解けるわけではありません。本記事で紹介するアプローチが、読者の皆さんがそのような問題に直面した際の解決の一助になれば幸いです。

概要

　リクルートでは、「タウンワーク」「ホットペッパービューティー」など、複数のフリーペーパーを全国の駅やコンビニエンスストアなどのラックに配置しています。各ラックへのフリーペーパーの配送は、複数の配送会社に委託しています。

　配送会社は複数のトラックで多くのラックを巡るので、その配送ルートを効率化することは重要な問題です。従来は人手によってトラックの配送ルートを決めていましたが、より効率的なルートを提案するために数理最適化を用いました。

ビジネス課題の理解

　ここでは、もう少し詳細に問題設定を説明します。

　トラックは配送会社の拠点から出発し、ラックを巡って、また拠点に戻ってきます。この際、全てのラックをいずれかのトラックで訪問する必要があります。

　下図は配送ルートのイメージです。

　決めるべきものは、次の2点です。

1. どのトラックがどのラックを担当するか
2. 各トラックはどのようなルートでラックを巡るか

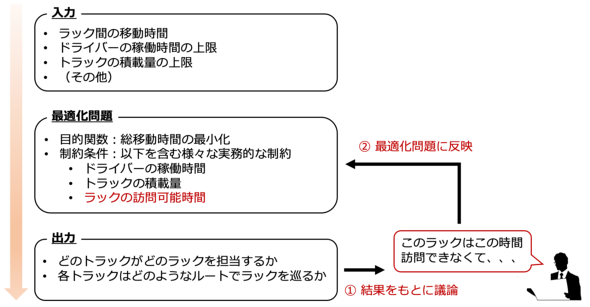
　ルートはできるだけ効率的なもの、すなわち、総移動時間が短くなるものが望ましいです。なお、ラック間の移動時間は入力データとして与える必要があります。

　さらに、次に挙げた項目などを含む多くの実務的な制約を守る必要があります。

• ドライバーの稼働時間
• トラックの積載量
• ラックを設置している店舗への訪問可能時間

　ここまでに説明した問題設定をまとめると、下図のようになります。

　このような複雑な問題を人間が考える大変さは想像に難くありません。しかし、人手だからこそ調整できる細かな要件があることも、また事実でしょう。現場の方に使っていただくために、「どれだけ現実に即した解を提案できるか」が本取り組みの肝といえます。

数理最適化によるアプローチ

　連載第2回でも述べた通り、最適化問題を考える際に、典型問題を参考にすることは有効なアプローチです。今回の問題では、「配送計画問題」（※1）が参考になります。本取り組みでは、配送計画問題の基本的な問題設定からはじめ、ヒアリングを通じて、より今回の問題に適した最適化問題にカスタマイズしていくというアプローチをとりました。

※1：「巡回セールスマン問題」は最適化問題の中でも有名な問題なので、聞いたことがある方もいるかもしれません。配送計画問題は巡回セールスマン問題の拡張と見ることができます。

　ところで、本連載で紹介した事例では、汎用の数理最適化ソルバーを用いて求解してきました。しかし、実は定式化した全ての最適化問題がソルバーで効率的に解けるわけではなく、問題によって得手不得手があります。今回扱う配送計画問題はソルバーが苦手とするタイプの問題です。そこで本取り組みでは、汎用のソルバーは使用せずに、今回の問題専用のソルバーを自前で開発することに決めました。

　以降では、ヒアリングを通じて最適化問題をカスタマイズする過程を説明し、次に、専用ソルバーの開発について説明します。

ヒアリングを通じた最適化問題のカスタマイズ

　配送計画問題は古くから研究されている問題であり、さまざまな拡張が提案されていますが、基本的な問題設定は次のようなものです。

• 状況設定
  • 拠点から出発した運搬車が、複数の顧客を経由して、また拠点に戻る
  • 顧客の位置は既知であり、各顧客は1回ずつ、いずれかの運搬車によって訪問される必要がある
  • 地点間の移動時間は既知である
  • 使用する運搬車の台数は事前に指定する
• 目的関数：運搬車の総移動時間の最小化
• 制約条件
  • 指定された運搬車の台数を守る
  • 全ての運搬車は拠点から出発し、拠点に戻ってくる
  • 全ての顧客を、ちょうど1台の運搬車が訪問する
  • 運搬車の積載量に上限がある
• 出力：各運搬車の最適な巡回ルート（※2）

※2：「ビジネス課題の理解」の節で掲載した図が出力のイメージです。

　本取り組みでは、上記の基本的な設定に多くの実務的な制約を追加し、実務で運用可能なルートの算出を目指します。

　具体的な制約はヒアリングを通じて決定しますが、単に「制約条件を全て列挙してください」といったコミュニケーションだけでは、必要な制約を全て得ることは難しいです。

　これを解決する方法の一つとして、結果を基に議論することが考えられます。例えば、「この結果を見て、実務で受け入れられない点を教えてください」といった具合です。本取り組みでは、このように現実に即さない点を解消する制約を一つずつ追加しました。

専用ソルバーの開発

　最適化問題を解く際のアプローチの指針として、大きく以下のように整理することができます。（参考：梅谷俊治先生の資料）

• 汎用解法：整数計画問題などに定式化して汎用ソルバーを適用する
• 専用解法：個々の問題の特徴を利用した専用ソルバーを開発する

　汎用解法は、「Gurobi」「CBC」といったソルバーを用いることができるので、開発が容易という利点がありますが、求解が苦手な最適化問題も少なくありません。一方で、専用解法は、個別に開発が必要なので手間がかかりますが、高い性能を期待できます。

　本節の最初でも述べた通り、配送計画問題は汎用解法で解くことは難しいので、ここでは専用ソルバーを開発しました。

　今回の問題は、効率的なルートを求める問題です。どのようにすれば効率的なルートが得られるでしょうか？

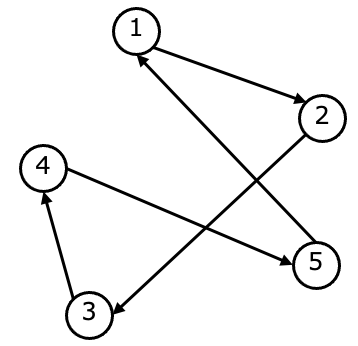
　まずは適当にルートを書いてみます。ここでは簡単のため、1つの巡回ルートのみに注目している点に注意してください。

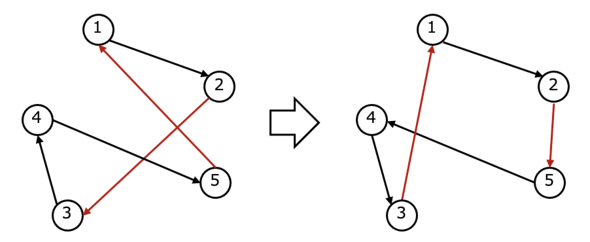
　ルートを表す矢印が入り乱れており、いかにも効率が悪そうに見えます。これをうまく改善していきましょう。一気に全てのルートを効率化するのは難しいので、2つの矢印だけに注目して、そこを改善します。例えば、下図において赤色で示した2つの矢印を入れ替えてみると、少し効率化したように見えます。

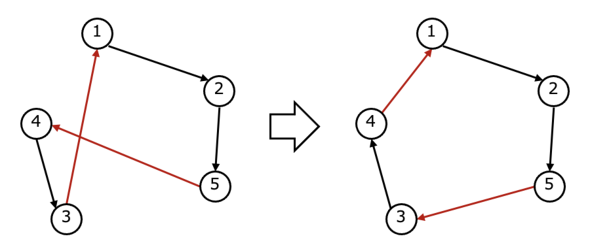
　もう少し続けてみましょう。今度は、下図の赤色で示した2つの矢印を入れ替えてみます。すると、矢印の交差はなくなり、効率的と思われるルートを得ることができました。

　このように局所的な改善を積み重ねる方法を「局所探索法」といいます。特に、上記の局所探索法は「2-opt法」といい、ルートを最適化する問題でよく用いられます。

　さらに、局所探索法を部品としてうまく用い、より高度な最適化を行うアプローチとして「メタヒューリスティクス」があります。今回の問題では、メタヒューリスティクスの一つ「アニーリング法」を用いて専用のソルバーを開発しました。

導入による効果

　本取り組みの結果として、従来の配送ルートよりも効率的なルートを発見することができ、現状より少ない車両台数でも配送できる見通しが得られました。

　配送会社としては、業務の効率化によって、ドライバー不足問題の解決が期待できます。リクルートとしては、継続的で安定的な配送業務の実施が期待できます。これは配送会社とリクルートの双方にとってメリットのある結果といえます。

おわりに

　以上、前回、前々回の連載から引き続き、リクルートでの数理最適化案件の実例を紹介しました。一口に「数理最適化」と言っても、案件によって最適なスタンスはさまざまなので、複数の案件をインプットすることでイメージを深める手助けになればと思っています。

筆者紹介

濱田賢吾

株式会社リクルート プロダクト統括本部　プロダクト開発統括室 データ推進室

2020年にリクルートに新卒入社。データサイエンティストとして、主に数理最適化施策の推進を担当。

棚橋 耕太郎

株式会社リクルート プロダクト統括本部　プロダクト開発統括室　データ推進室

リクルートに入社後、広告配信システムの開発に従事。その後アドバンスドテクノロジーラボに兼務し、量子アニーリングの研究なども行っている。