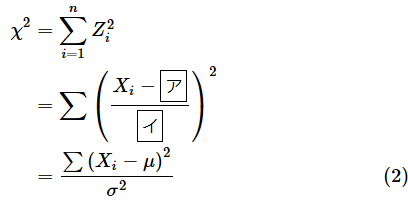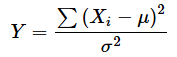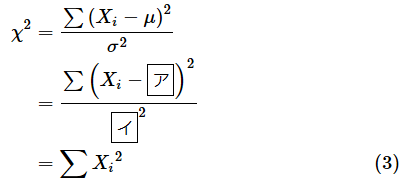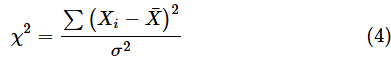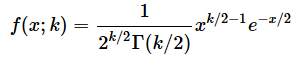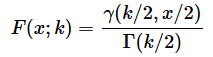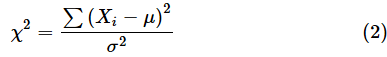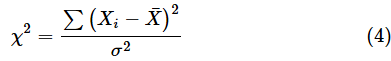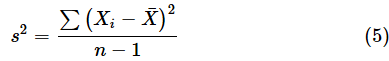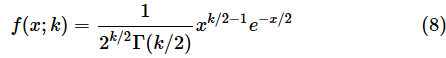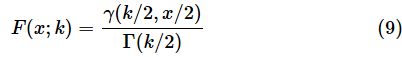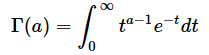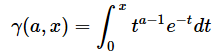［データ分析］カイ二乗分布 〜 ポテトチップスの内容量のばらつきは改善されたか？：やさしい確率分布

データ分析の初歩から学んでいく連載（確率分布編）の第7回。カイ二乗分布は標準得点の二乗和の分布です。標準得点とは何か、二乗することはどういう意味を持つのか、といった基本的なところからカイ二乗分布の姿を明らかにしていきます。続けて、確率密度関数や累積分布関数の求め方や可視化の方法を解説し、利用例などを紹介します。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第7回です。前回は、連続型確率分布の代表とも言われる正規分布を取り上げました。今回はカイ二乗分布について、その特徴や意味を基本から解き明かし、確率密度関数／累積分布関数の求め方、利用例などを見ていきます。

ばらつきはどう分布するのか 〜 カイ二乗分布につながるイメージ

　前回お話しした中心極限定理を覚えているでしょうか。母集団がどのような分布であっても、そこから幾つかのサンプル（標本）を取り出して、そのサンプルの平均値を求めることを繰り返すと、それらの平均値の分布が正規分布に近づくというものでしたね。つまり、サンプルの平均値が正規分布に従っているということでした。

　であれば、サンプルの「平均値」が正規分布に従うように、サンプルの「分散」も何らかの分布に従うのか知りたいですよね。答えから言うとカイ二乗分布に従うのですが、順を追って見ていきましょう（正確には、標準正規分布から得られたサンプルの二乗和が確率変数となり、それがカイ二乗分布に従います。そのことを確認するためにも一歩ずつ進めましょう）。

　ポイントとなるのはカイ二乗分布の確率変数はどのようなものであるかということとカイ二乗分布の確率密度関数と累積分布関数はどのようなものであるかという2点です。まず、確率変数からお話ししていきます。

　統計学では、○○分布に「従う」という表現がよく出てきます。この「従う」という言葉は「規則に従う」といった意味の「従う」です。例えば「カイ二乗分布に従う」というのは、「確率変数の値が、カイ二乗分布する母集団から取り出されたものである」あるいは「確率変数の分布が理論的にはカイ二乗分布に当てはまるはずだ」といった意味です。なお、統計学では「従う」を∼という記号で表します（後で登場します）。

　具体的な問題で考えてみます。最初に何を知りたいかをイメージしておこうというわけです。あくまで架空の事例ですが、あるお菓子の内容量について、母集団の平均が100g、標準偏差が0.5gで、正規分布に従っていることが分かっているものとします。さて、このお菓子をn個取り出して内容量を測定したとき、その分散（を基に得られる確率変数）はどう分布するでしょうか（図1）。

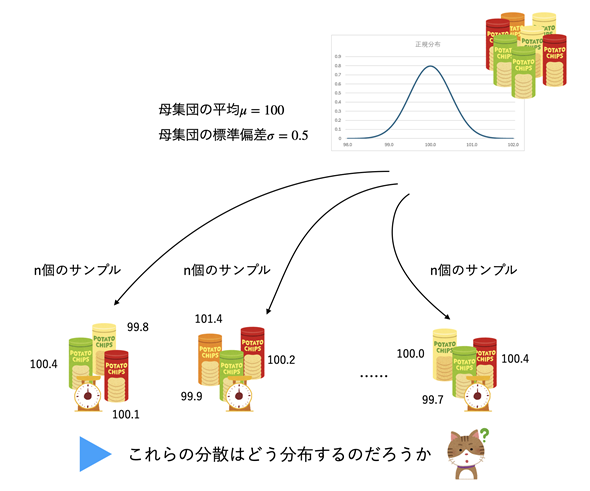図1　分散はどんな分布になるのかを考えてみよう
前回は、サンプルの平均は正規分布に従うことを解説した。では、分散はどのような分布に従うのだろうか。それを知るためにはカイ二乗分布の確率変数がどのようなものかを理解することから見ていく必要がある。

　前述したように、カイ二乗分布の確率変数がどのようなものであるかについて理解を深めてからでないと答えが出ないので、少しずつお話しします。先にカイ二乗分布の確率密度関数や累積分布関数がどのようなものかを知りたい方はこちらをご覧ください。

カイ二乗分布はどこから現れるのか 〜 カイ二乗分布の確率変数

　では、カイ二乗分布の確率変数について見ていきます。出発点は母集団の分布が正規分布であるという前提からです。

　図1で見たように、正規分布する母集団からn個のサンプルを独立に（ある試行が他の試行に影響しない取り出し方で）取り出します。確率変数をXとすると、それらは、X₁, X₂, ... , X_nで表されます。小文字のxではなく、大文字のXを使っているのは、個々の具体的な値を考えているわけではなく、「確率変数である」ということを一般的に表しているからです。

母平均が分かっている場合のカイ二乗値とカイ二乗分布

　基準を統一して、各サンプルが平均からどれだけ離れているかを知るには、標準得点を求めればいいですね。以下のように平均値μを引いて、標準偏差σで割れば求められます。一歩ずつ確実に理解できるように、穴埋め問題にしておくので、何が入るかを考えながらゆっくり読み進めてみてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます（以下同様です）。

　答え： ア＝　μ　、イ＝　σ　

　ここで、それぞれの値が平均からどれだけ離れているかを合計したいのですが、標準得点Z_iは正になる場合もあれば、負になる場合もあるので、そのまま合計すると正と負が相殺されてしまいます。そこで、全てを正にするために二乗和を求めることにしましょう。つまり、二乗して合計するわけです（いつもの手ですね）。

　このようにして求められた値をカイ二乗値と呼び、χ²と表します。つまり、以下のようになります。Σの部分については、2行目以降、式を見やすくするためにiの値の範囲を省略して表記してあります。

　答え： ア＝　μ　、イ＝　σ　

　このχ²という確率変数は自由度nのカイ二乗分布χ_(n)²に従います（自由度とは単にサンプルの個数ということではなく、独立した情報の個数に当たるものです。後で詳しく解説します）。確率変数と分布の名前に同じ文字を使っているので同語反復っぽくなりますが、（2）式の左辺を別の文字で表すと分かりやすくなります。例えば、Yで表すと、

となります。この確率変数Yが自由度nのカイ二乗分布に従うということですね。統計学では「従う」を∼という記号で表すので、このことを数式で表すと以下のようになります。左辺がカイ二乗値（確率変数）、右辺のχ_(n)²が自由度nのカイ二乗分布です。

　なお、標準正規分布ではμ＝0、σ＝1なので、Xがそのまま標準得点になります。従って、カイ二乗値χ²は以下の式で求められます。（2）式にμ＝0、σ＝1を代入して確認してみましょう。

　答え： ア＝　0　、イ＝　1　

　標準正規分布から得られたサンプルの二乗和が確率変数となっています。そして、それが自由度nのカイ二乗分布に従います。これで、最初のお話とつながりましたね。

　しつこいようですが、（2）式や（3）式で求められるカイ二乗値χ²は確率変数です。つまり、確率密度関数や累積分布関数の横軸に当たるものです。要するに、カイ二乗分布に従う確率変数なので、カイ二乗値と呼ばれるということです。カイ二乗値に対する確率密度関数の値や累積分布関数の値、つまり縦軸の値は、後で登場するExcelのCHISQ.DIST関数で求められます。

　カイ二乗分布の確率密度関数や累積分布関数がどのようなものになるかは、次の項でお話しします。もう少しだけ確率変数（カイ二乗値）のお話をしておきます。

母平均が分からない場合のカイ二乗値とカイ二乗分布

　ところで、上の例は

があらかじめ分かっている場合のお話です。母平均μが分からない場合には、

を代わりに使ってカイ二乗値χ²を求めます。その場合は自由度がn−1となります。つまり、カイ二乗値は、

となります。母平均が分からない場合は、（4）式で求められるカイ二乗値χ²が、自由度n−1のカイ二乗分布χ²_(n−1)に従います。

自由度っていったい何？　何が自由なの？

　さて、ここでカイ二乗分布の自由度としてnを使ったりn−1を使ったりするのを、腑（ふ）に落ちないと感じた人も多いと思います。その前にそもそも自由度とはどのような値なのかが謎ですね。

　端的に言うと、自由度とは独立した情報（変数）の個数のことです。では、独立した情報というのは何なのでしょうか。具体的に見ていきます。

　（4）式では、

は、n個のデータX₁〜X_nを基に求められます。つまり、

を求めるために、それぞれのデータから1/n個ずつの情報をもらっています。

の情報の個数は(1−1/n)個、

の情報の個数も(1−1/n)個……ということですね。これがn個あるので情報の個数は全部で(1−1/n)× n ＝ n−1個になるというわけです。

の部分には、見た目ではn個の変数がありますが、独立した情報はn−1個しかないということになります。

　自由度は、「自由に動かせる変数の個数」と説明されることもあります。具体的な数値で考えてみます。

　例えば、10, 12, 17という3個のサンプルから平均値を求めると、

です。平均が13のとき、10と12という2個の値を決めると、17という値は自動的に決まってしまいます。ここで仮に10と12を11と8に変えたとしても、

の「？」の部分は、やはり自動的に20に決まります。つまり、自由に動かせるのは3−1＝2個となります。

　一方、あらかじめ母平均μが分かっている場合は、μはサンプルから求めた値ではなく、それぞれのサンプルとは別に決まっている値なので、（2）式のΣ(X_i−μ)の部分にはn個の独立した情報があると考えられます。

　自由度はカイ二乗分布だけでなく、次回解説するt分布やF分布でも登場します。それぞれの手法や分布での自由度の考え方はなかなか理解しづらいものですが、実用的には「こういう手法や分布の場合には、自由度はいくら（例：n−1）とする」といったルールで覚えておくのが、最も悩まなくて済む付き合い方ではあります。

　カイ二乗分布の確率変数と自由度のお話はこれぐらいにして、カイ二乗分布の確率密度関数と累積分布関数がどのようなものであるかを可視化してみましょう。

カイ二乗分布ってどんな感じの分布（1）〜 確率密度関数を可視化してみよう

　ここまでは、カイ二乗分布の確率変数であるカイ二乗値χ²をどのようにして求めるかというお話をしてきました。では、カイ二乗値分布では確率変数がどのように分布するのでしょうか。つまり、確率密度関数と累積分布関数はどのようなものになるのでしょうか。

　実は、カイ二乗分布の確率分布関数f(x; k)の値と累積分布関数F(x; k)の値は以下の式で求められます。しかし、これらの式を覚える必要は全くありません。詳細については最後のコラムでお話しするので、ここでは式を掲載するだけにとどめます。以下の式は軽くスルーしてもらってけっこうです。

　上の式を覚えなくても、ExcelのCHISQ.DIST関数を使えば、確率密度関数の値と累積分布関数の値が簡単に求められます。カイ二乗分布の母数は自由度のみです。つまり、自由度が決まれば、カイ二乗分布の形も決まります。CHISQ.DIST関数の形式（図2）を見てから、確率密度関数の値を求め、カイ二乗分布を可視化しましょう（累積分布関数については次の項で取り扱います）。

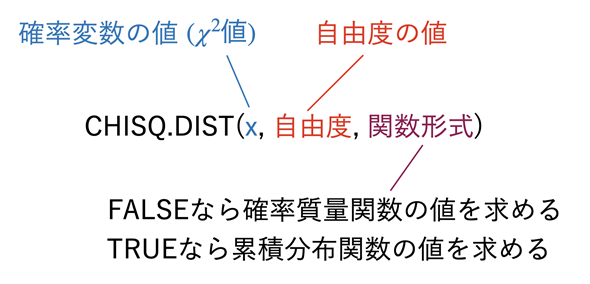図2　CHISQ.DIST関数に指定する引数
CHISQ.DIST関数には、確率変数の値（χ²値）と自由度を指定する。関数形式についてはこれまで見てきた関数と同様、FALSEを指定すれば確率密度関数の値が、TRUEを指定すれば累積分布関数の値が求められる。

　以下に、幾つかの自由度に対する確率密度関数の値を求め、それらのグラフを描いてみます（図3）。作成の手順は図の後に記しておきます。

図3　カイ二乗分布の確率密度関数の例
自由度1, 2, 5, 10, 20について、x＝0.0〜20.0までの確率密度関数の値を求め、グラフを描いてみた。自由度が1のとき、x＝0に対する確率密度関数の値は求められないので、セルB5にはエラー値が表示されている。そのため、グラフはセルB5を除外して描いている。作成の手順は後の箇条書きを参照。

　カイ二乗分布の台（確率変数が取り得る値の範囲）は0〜∞です。そもそも、二乗した値の合計なので負になることはありませんね。また、自由度kが大きくなると、x＝kの近くで確率密度関数のピーク（山の頂点）が見られるようになり、左右に裾野が広がる形になります。例えば、自由度が10の場合、グラフの横軸がx＝10となる位置の近くに山のある分布となります（といっても、自由度をもっと大きくしないとx＝kの位置がピークにならないのですが、雰囲気はつかめると思います）。実は、カイ二乗分布は、自由度kを大きくしていくと、

に近づきます（近づき方はそれほど早くないので、kの値をかなり大きくしないと、正規分布のグラフには重なりません）。

　ここでは、自由度を表すのにkという文字を使いましたが、これは、離散型確率分布の確率変数の値を表すのに使われるkとは全く別のものです（念のため）。なお、自由度を表す文字としては、ギリシア文字のν（ニュー）などを使うこともあります。νはラテン文字（アルファベット）のnに当たる文字です。自由度はdegree of freedomを略してdfと表記されることもあります。

　確率密度関数の値を求めるための手順は以下の通りです。可視化については単に折れ線グラフを描くだけなので（前回までですでに何度もやっているので）、今回からは関数の入力にのみ焦点を当てることとして、グラフ作成などの手順についてはサンプルファイル内に掲載しておくこととします。

　サンプルファイルをこちらからダウンロードし、［カイ二乗分布］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

◆ Excelでの操作方法

• セルB5に=CHISQ.DIST(A5:A105,B4:F4,FALSE)と入力する
  • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB5〜F105）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• 5行目のみ手作業で数値を入力する
  • セルB5に「#NUM!」というエラー値を入力しておく
  • セルC5に0.5を入力しておく
  • セルD5〜F5に0を入力しておく
• セルB6に「=ARRAYFORMULA(CHISQ.DIST(A6:A105,B4:F4,FALSE))」と入力する

　原因は不明ですが、原稿の執筆時点ではx=0.0,自由度=2のとき、GoogleスプレッドシートのCHIDSQ.DIST関数では確率密度関数の値（0.5）が正しく求められず、エラーとなります。上の手順で5行目だけを手作業で入力して6行目以降をCHISQ.DIST関数で求めたのはそのためです。

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

カイ二乗分布ってどんな感じの分布（2）〜 累積分布関数を可視化してみよう

　続いて、累積分布関数です。こちらは、自由度5の例だけを見ておきます（図4）。確率密度関数でグラフとx軸で囲まれた範囲の面積が累積分布関数の値になることを示すために、確率密度関数も併せて作成し、説明をグラフ上に書き加えてあります。［カイ二乗累積分布］ワークシートを開き、図の後に記した手順で試してみてください。グラフ作成などの手順についてはサンプルファイル内に掲載しておくこととします。

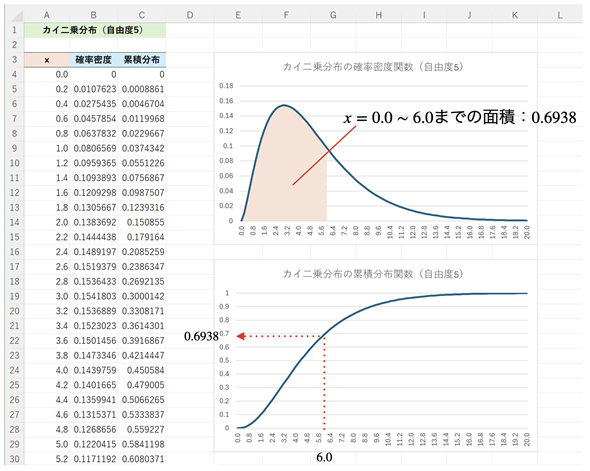図4　カイ二乗分布の累積分布関数の例
上のグラフが確率密度関数のグラフ。グラフとx軸で囲まれた範囲の面積が累積分布関数の値になる。下のグラフは、その面積、つまり累積分布関数の値をプロットしたもの。例えば、x＝6.0に対する累積分布関数の値は0.6938となる。

　確率密度関数の値を求める方法はすでに見た通りですが、x＝0.0〜6.0の範囲を塗りつぶして表示するために使うので、以下に併せて見ておきます。

◆ Excelでの操作方法

• 確率密度関数の値を求める
  • セルB4に=CHISQ.DIST(A4:A104,5,FALSE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB4〜B104）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

• 累積分布関数の値を求める
  • セルC4に=CHISQ.DIST(A4:A104,5,TRUE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルC4〜C104）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• 確率密度関数の値を求める
  • セルB4に=ARRAYFORMULA(CHISQ.DIST(A4:A104,5,FALSE))と入力する

• 累積分布関数の値を求める
  • セルC4に=ARRAYFORMULA(CHISQ.DIST(A4:A104,5,TRUE))と入力する

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

コラム　カイ二乗分布の確率密度関数をシミュレーションで求める

　すでにお話ししたように、カイ二乗値を求めるには、正規母集団（＝正規分布の母集団）からn個のサンプルを取り出し、それらの標準得点の二乗和を求めます。ということは、その手順に従ってカイ二乗値を幾つも作り、ヒストグラムを描くとカイ二乗分布に近くなるはずですね。冒頭の例で示した平均μ＝100と標準偏差σ＝0.5を使ってもいいのですが、結局のところ、標準化した値を使うので、最初から標準正規分布（μ＝0, σ＝1の正規分布）を使ってシミュレーションしてみましょう。

　シミュレーションはExcelでもできますが、多数のセルを使う必要があり、ちょっと面倒です。一応、サンプルファイルに作成例は含めてありますが、特に解説はしません（［カイ二乗分布のシミュレーション］ワークシート）。そこで、Pythonのプログラムを使うことにします（リスト1）。

　サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。結果は図5のようになります。コードの詳細については解説しませんが、コメントとリスト1の説明を見れば何をやっているかが大体分かると思います。

# カイ二乗分布の確率密度関数のシミュレーション
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2

# 標準正規分布（μ=0、σ=1）からランダムに10個のサンプルを取り出したものを10000個作り、それぞれ二乗する
x = np.random.randn(10000, 10)**2
chi2_sample = x.sum(axis=1)  # 各行を合計する。これがカイ二乗値（横軸）

# ヒストグラムを描く（カイ二乗値がどのように現れるかが分かる）
plt.hist(chi2_sample, bins=100, density=True)  # 階級は100個、縦軸は確率とする

# カイ二乗分布の確率密度関数を描く
x = np.linspace(0, 40, 100)  # 0〜40までを100個に分けた等差数列（横軸の値）
plt.plot(x, chi2.pdf(x, 10))  # xに対する確率密度関数の値をプロットする
plt.show()

リスト1　カイ二乗分布の確率密度関数をシミュレーションする
標準正規分布（μ＝0、σ＝1）からランダムに10個の値を取り出すことを10000回繰り返す。10000行×10列のデータが作られるので、それらの値を全て二乗する。各行を合計すれば、10個のデータを合計したものが10000行作られることになる。この10000行のデータがカイ二乗値になる。続いて、縦軸を確率としてカイ二乗値のヒストグラムを描く。最後に、自由度10のカイ二乗分布の確率密度関数を描けば、ヒストグラムとほぼ重なることが分かる。

　リスト1の実行例が以下の図5です。乱数を使うので結果は毎回少しずつ異なりますが、ほとんど重なっていますね。

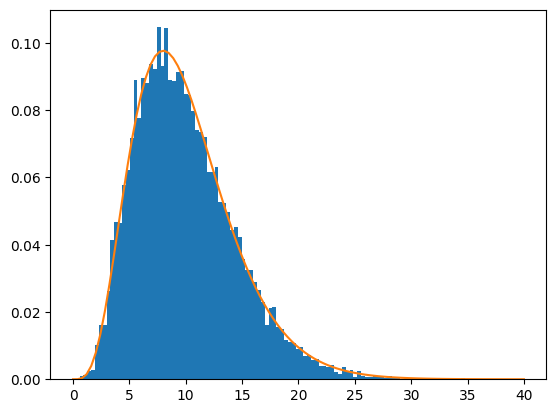図5　カイ二乗分布の確率密度関数のシミュレーション結果
棒グラフは、標準正規分布から10個のサンプルを10000回取り出して、それらの二乗和を基に作成したヒストグラム。折れ線グラフは自由度10のカイ二乗分布の確率密度関数。

カイ二乗分布の応用に向けて 〜 区間推定や検定のための準備

　カイ二乗分布は母分散の区間推定や母分散の検定、いわゆるカイ二乗検定（適合度の検定や独立性の検定）などに使われます。詳細は推測統計編でお話ししますが、その準備として、少し発展的なお話をしておきましょう。カイ二乗分布のさらなる理解にもつながります。

　母平均が既知の場合、カイ二乗値は以下の式で求められました。（2）式を再掲します。この場合は、定義通りに計算してカイ二乗値を求める必要があります。

　一方、母平均が未知の場合には、もう少し簡単に計算する方法があります。母平均が未知の場合、カイ二乗値は以下の式で求められました。（4）式を再掲します。

　ここで、以下のようなs²を考えます（これはExcelのVAR.S関数で求められる不偏分散です）。

　（5）式の両辺にn−1を掛けて以下のように変形しましょう。

　（6）式の左辺を（4）式に代入すると、以下のようになります。

　このことから、母平均が未知の場合は、（4）式の通りに計算しなくても、VAR.S関数によって求めた不偏分散にn−1を掛け、母分散で割るだけで、カイ二乗値が求められることが分かります。このようにして求めたカイ二乗値が自由度n−1のカイ二乗分布に従うということですね。

ばらつきは小さくなったのか？ 〜 母平均が未知の場合の累積確率を求める

　では、冒頭のお話の続きです。これまでの製品は、母平均が100g、母標準偏差が0.5gでした。そこで、内容量が少な過ぎたり多過ぎたりする製品（不良品）の発生を減らすために製造工程を見直したとします。つまり、製品のばらつきを小さくするために工程を見直したというわけです。工程の見直し後、10個のサンプルを取り出して内容量を測定したところ、以下のような値になったとします。さて、内容量のばらつきは改善されたでしょうか。

100.1, 100.0, 99.8, 100.0, 99.7, 99.8, 99.9, 100.4, 100.3, 100.2

　工程の変更によって原料の配分や水分の量なども変わった可能性があるので、母平均も変わったかもしれません。従って、母平均は既知ではなく、未知であるものと考えることにします（実際のところ、母平均が分かっている場合よりも、分からない場合の方が多いですね）。

　まず、これらの値を基に不偏標準偏差（母標準偏差の推定値）を求めてみましょう。［応用例1（母平均未知）］ワークシートを開き、セルA18に=STDEV.S(A6:A15) と入力してください（図6）。不偏標準偏差を求めるためのSTDEV.S関数や不偏分散（母分散の推定値）を求めるためのVAR.S関数については、「やさしいデータ分析］分散／標準偏差〜給与の格差ってどれぐらい？」で解説したので、そちらもぜひご参照ください。

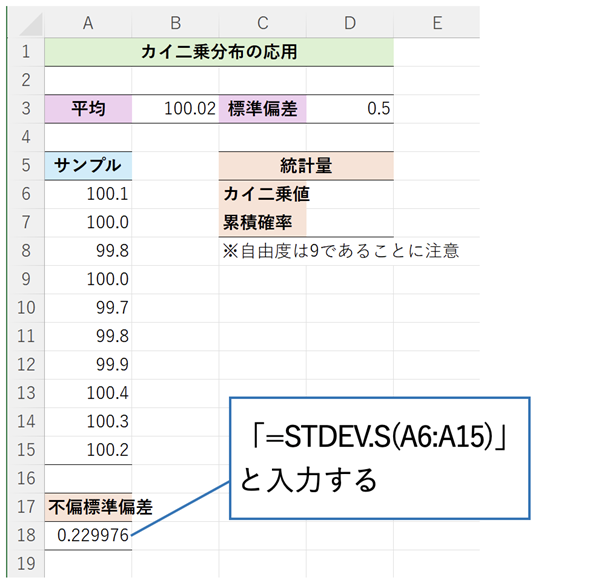図6　不偏標準偏差を求めて、母集団の標準偏差を推定する
母集団のばらつきを推定するために、不偏標準偏差を求めるためのSTDEV.S関数を使う。セルA18に=STDEV.S(A6:A15)と入力すれば、0.229976（≈0.230）となる。これまでの0.5という値よりも小さくなっているように思われるが、本当に小さくなったのだろうか。

　不偏標準偏差は0.230g（不偏分散はその二乗なので0.053）となりました。これまでの標準偏差が0.5gだったので、ばらつきは小さくなったように思われます。……が、そう判断していいのでしょうか。そこで、母標準偏差が0.5g（母分散は0.25）である母集団からサンプルを取り出したときに、上のような値（セルA6〜A15の値）が現れる確率を求めてみましょう。そのために、カイ二乗値とカイ二乗分布の累積分布関数の値を求めてみます（あまりにも確率が小さいようであれば、母標準偏差は0.5gとは考えにくい、つまり母標準偏差が小さくなった、と言えますね）。

　この場合、カイ二乗値は（4）式に従って計算するよりも、（7）式を使った方が簡単です。（7）式を再掲します。

　［応用例1（母平均未知）］ワークシートを続けて使います。図7の手順に沿って計算してみましょう。s²はVAR.S関数で求めます。n−1の値は10-1=9で、σの値はセルD3に入力されている標準偏差を二乗すれば求められますね。カイ二乗値が求められたら、それを基にCHISQ.DIST関数を使ってカイ二乗分布の累積分布関数の値（累積確率）を求めます。

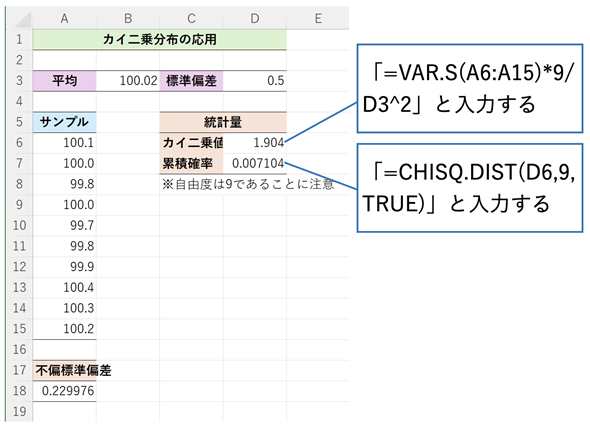図7　新しい製造工程での分散は母分散と等しいか（母未知が既知の場合）
（7）式に従って、セルD6に=VAR.S(A6:A15)*9/D3^2と入力するだけで、カイ二乗値が求められる。この場合、自由度は9なので、セルD7に=CHISQ.DIST(D6,9,TRUE)を入力してカイ二乗分布の累積分布関数の値を求める。

　カイ二乗値は1.904となり、それに対するカイ二乗分布の累積分布関数の値は0.0071（0.71％）になります。この結果を見ると、かなり「まれ」なことが起こったことが分かります。母標準偏差が0.5（母分散が0.25）だとすると、10個のサンプルを取り出して、それらの値から求めた不偏標準偏差が0.230である（不偏分散が0.053）であるというのはそうそう起こらないことです。ということは、製造工程を見直した場合の母分散は0.25よりも小さくなったと考えられます。つまり、内容量のばらつきが小さくなったものと考えられます。

　上で求めた累積確率を可視化した図（図8）も［応用例1（母平均未知完成例）］ワークシートに含めてあります。こちらについてはワークシート内に作成方法を記載しておきます。

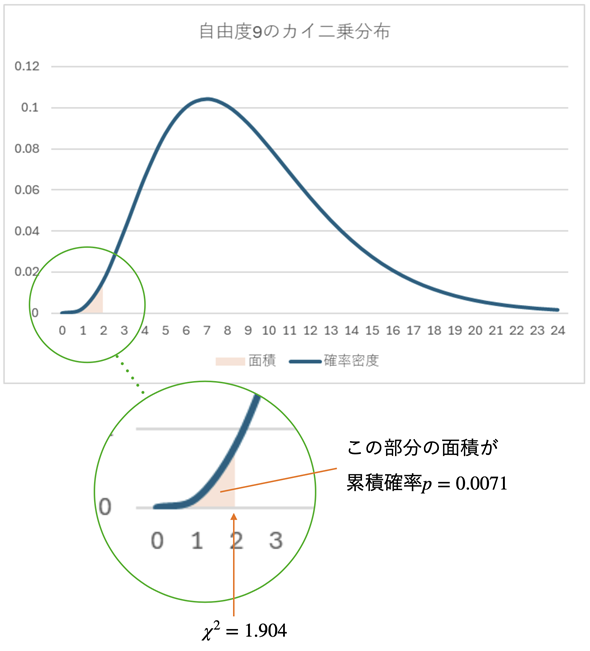図8　カイ二乗値1.904に対する累積確率
オレンジ色で塗りつぶした部分の面積が累積確率（0.0071＝0.71％）。分散が小さくなるとカイ二乗値も小さくなるが、カイ二乗値が1.904になるのはかなり「まれ」なこと（確率変数の値がグラフの端の方に位置していて、面積が小さい）。新しい製造工程では内容量のばらつきが小さくなったものと考えられる。

　実は、この計算は母分散の検定のための計算にほかなりません。検定の考え方や詳細な方法については、推測統計編でのお話となるので、ここでは、これ以上のお話はしません。帰無仮説や対立仮説などの考え方を十分に知った上で使う必要があるので、この時点で「結論はこうだ！」と言い切るのは少し待ってください。もったいぶるようで申し訳ないのですが、母分散の検定については（さらには適合度の検定、独立性の検定などについても）、推測統計編でお話しします。

　なお、（7）式は、F分布やt分布にもつながる式です。今回は、カイ二乗分布の確率変数とはどのようなものか、それに対する確率密度関数や累積分布関数の値はどのようにして求めるか、を理解していただければと思います。

　逆に、ばらつきが大きくなってしまった場合には、どのような値になるでしょうか。例えば、サンプルの値が以下のようになっていたとします。

100.9, 100.1, 100.2, 100.0, 98.4, 99.6, 99.5, 100.3, 100.2, 101.0

　こちらは［応用例2（分散が大きい場合）］ワークシートに作成してあります。計算方法は全く同じなので、結果だけを記すと、カイ二乗値は19.824となり、その値に対するカイ二乗分布の累積確率は0.98097（＝98.10％）となります。この確率は下位からの確率なので、上位からだと0.01903（1.90％）ですね。このようにカイ二乗値が大きな値になることも、やはり「まれ」なことなので、母集団の分散は0.25よりも大きいと考えられます。

　なお、上位からの累積確率（右側確率または上側確率と呼ばれます）を求めるには1からCHISQ.DIST関数で求めた値を引いてもいいですが、CHISQ.DIST.RT関数を使うと簡単です。こちらは、セルD10に入力した=CHISQ.DIST.RT(D6,9)で求められます（カイ二乗値と自由度を指定するだけです。累積確率を求めることが分かっているので関数形式の指定は不要です）。

　ところで、母平均が既知の場合はどうなるでしょうか。つまり、母平均が100gであると分かっている場合です（現実には、そういう場合は少ないですが）。その場合は（2）式に従って計算します。サンプルファイルの［応用例3（母分散既知完成例）］に作成方法と併せて作成例を掲載しています。

カイ二乗分布の累積分布関数に対する逆関数は？

　CHISQ.INV関数やCHISQ.INV.RT関数を使えば、カイ二乗分布の累積分布関数に対する逆関数の値が求められます。CHISQ.INV関数には左側（下側）確率と自由度を指定し、CHISQ.INV.RT関数には右側（上側）確率と自由度を指定します。

　例えば、自由度10のカイ二乗分布で、累積確率が95％のときのχ²値は=CHISQ.INV(95%, 10)または=CHISQ.INV.RT(5%, 10)で求められます。空いているセルにこれらの式を入力してみてください。いずれも18.307という値が求められます。これらの例は［カイ二乗分布の逆関数］ワークシートに入力されています。

　カイ二乗分布の累積分布関数に対する逆関数の値は、母分散の区間推定などに使われます。詳細は推測統計編でお話しします。

コラム　カイ二乗分布の確率密度関数と累積分布関数を数式で表す

　カイ二乗分布の確率密度関数f(x; k)と累積分布関数F(x; k)は以下の式で表されます。ここでは、自由度kを;で区切って示してあります。例によって、これらの式を無理に覚える必要はありません。上で見たように、いずれもExcelのCHISQ.DIST関数で答えが求められます。

　ただし、

　Γはガンマ関数と呼ばれるもので、階乗（n!）の考え方を複素数にまで拡張したものです。γは下側不完全ガンマ関数または第一種不完全ガンマ関数と呼ばれるもの（ガンマ関数の定義域である0〜∞のうち、下部の0〜xに対する値を求める関数）ですが、数学的な話にはこれ以上深入りしないことにします。

　Excelを使って上の定義通りに計算することもできます。ガンマ関数の値については、ExcelのGAMMA関数を使えば求められるので、やや複雑になりますが（8）式を使って確率密度関数の値を求めることができます。一方の累積分布関数については、Excelに不完全ガンマ関数がないので（9）式の定義通りに計算するのはちょっと面倒です（積分の近似値を求める必要があります）。いずれも、サンプルファイルに参考として含めておきますが、ここはPythonのプログラムを使った方が簡単なので、その例を紹介します。

　（8）式や（9）式に登場するガンマ関数の値を求めるには、scipy.specialモジュールのgamma関数を使い、下側不完全ガンマ関数の値を求めるにはscipy.specialモジュールのgammainc関数を使います。実は、gammainc関数では、正則化された（ガンマ関数で割り算した）下側不完全ガンマ関数の値が求められます。つまり、（9）式の分子の部分ではなく、（9）式そのものの値が求められます。というわけで、scipy.specialモジュールのgammainc関数の結果はカイ二乗分布の累積分布関数の値と一致します。

　サンプルプログラムはコラムで紹介したシミュレーションの続きに入力されています。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。2番目以降のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。コードの詳細については解説しませんが、コメントとリスト2の説明を見れば何をやっているかが大体分かると思います。

# 定義に従って、カイ二乗分布の確率密度関数の値を求める
from scipy.special import gamma
import numpy as np

k = 5  # 自由度
x = 3  # 確率変数の値
print(1​/(2**(k/2)*gamma(k/2)) * x**(k/2-1) * np.exp(-x/2))  # 定義通りに計算

# 出力例：
# 0.15418032980376925

# 検算
from scipy.stats import chi2

print(chi2.pdf(x, k))  # カイ二乗分布の確率密度関数

# 出力例：
# 0.15418032980376925

# 定義に従って、カイ二乗分布の累積分布関数の値を求める
from scipy.special import gammainc

print(gammainc(k/2, x/2))  # 正則化された下側不完全ガンマ関数を使って定義通りに計算

# 出力例：
# 0.3000141641213724

# 検算
from scipy.stats import chi2

print(chi2.cdf(x, k))  # カイ二乗分布の累積分布関数

# 出力例：
# 0.3000141641213724

リスト2　定義に従ってカイ二乗分布の確率密度関数と累積分布関数の値を求める
ここでは、自由度k＝5、確率変数の値x＝3で計算してみた。確率密度関数については、（9）式をそのまま書けばよい。累積分布関数については、scipy.specialモジュールのgammainc関数を使って正則化された下側不完全ガンマ関数を求めるとよい。その結果が累積分布関数の値と一致する。

---

　今回はカイ二乗分布での確率変数であるχ²値の意味やその求め方、さらに、カイ二乗分布の確率密度関数と累積分布関数の求め方などについてお話ししました。推測統計編の内容についても、かなり踏み込んでお話ししてしまいました。カイ二乗分布は、分散の比を表すF分布や、平均値の推定などに使われるt分布とも深く関わっているので、ここでは、カイ二乗分布の確率変数と確率密度関数、累積分布関数についての理解を深めていただければ十分かと思います。

　というわけで、次回はt分布についてお話しします。次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

カイ二乗分布の確率密度関数や累積分布関数の値を求めるための関数

CHISQ.DIST関数： カイ二乗分布の確率密度関数や累積分布関数の値を求める

形式

CHISQ.DIST(x, 自由度, 関数形式)

引数

• x： 確率変数の値（カイ二乗値）を指定する。
• 自由度： 自由度を指定する。
• 関数形式： 以下の値を指定する。
  • FALSE …… 確率密度関数の値を求める
  • TRUE …… 累積分布関数の値を求める

備考

※ 累積分布関数の値は左側確率（または下側確率）とも呼ばれます。

CHISQ.DIST.RT関数： カイ二乗分布の右側確率の値を求める

形式

CHISQ.DIST.RT(x, 自由度)

引数

• x： 確率変数の値（カイ二乗値）を指定する。
• 自由度： 自由度を指定する。

備考

※1から、CHISQ.DIST関数で求められる累積分布関数の値を引いた値が返されます。

カイ二乗分布の累積分布関数に対する逆関数の値を求めるための関数

CHISQ.INV関数： カイ二乗分布の累積分布関数に対する逆関数の値を求める

形式

CHISQ.INV(累積確率, 自由度)

引数

• 累積確率： 累積分布関数の値を指定する。
• 自由度： 自由度を指定する。

備考

※累積確率には左側確率（下側確率）の値を指定します。

CHISQ.INV.RT関数： カイ二乗分布の右側確率に対する逆関数の値を求める

形式

CHISQ.INV.RT(右側確率, 自由度)

引数

• 右側確率： 累積分布関数の右側確率の値を指定する。
• 自由度： 自由度を指定する。

備考

※右側確率は1−左側確率です。

「やさしい確率分布」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう