EclipseでJavaの型を理解する:EclipseでJavaに強くなる(5)(1/3 ページ)
コンピュータは基本的に0と1しか扱えないために、人間が使っている十進数や文字を表現するためにはいろいろと工夫をする必要があります。また、情報を保持するための記憶装置や補助記憶装置は有限な資源ですから、整数を表現するにしても扱える最大値を制限するなど、いろいろな制約をする必要があります。多くのプログラミング言語では、型という仕組みを使って、これらの工夫や制約といったことをどうするかについてあらかじめ決めています。今回は「型を決めることによって、どうやって0と1だけを使っていろいろなデータを表現しているか」ということについて理解を深めましょう。
(連載Eclipseではじめるプログラミングの「第3回 Javaの変数の型と宣言を理解する」「第9回 Javaの参照型変数を理解する」も参考にしてください。)
整数型(Integral Type)
二進数と十六進数
まず、コンピュータは基本的に0と1しか扱えないということについてあらためて考えてみましょう。0と1しか扱えませんから、コンピュータに数値計算をさせるためには、これらを使って数を表現することになります。0と1だけを使って数を表現するには二進数を使います。下記の表のように、十進数が0から9までの数字を使って10ごとにけたが上がるのに対して、二進数は0と1の数字を使って2ごとにけたが上がります。
| 十進数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 二進数 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
ここで、見てのとおり二進数を使うと小さい数でもけた数が大きくなってしまいます。ですから、プログラミングでは十六進数を使うことが多くなります。その場合は16文字が必要になるので、AからFまでの6文字を順に10から15へ対応させて、0から9までの10個の数字へ加えて表現をします。例えば、十進数の8から17を十六進数へ対応させると次のようになります。
| 十進数 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|
| 十六進数 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
さて、ここで二進数の10(十進数での2)と、十進数の10と、十六進数の10(十進数での16)をどうやって区別するのか不思議に思うはずです。1つの方法としては、基数(二進数の場合は2、十進数の場合は10、十六進数の場合は16)を数値の右下へ丸括弧付きで表記します。この表記を使えば、二進数の10は10(2)、十進数の10は10(10)、十六進数の10は10(16)と書くことにより区別をすることができます。普通は十進数をよく使うので、基数が省略された場合は断りがない限り十進数を表します。
プログラミング言語では十六進数をよく使うため、10(16)と表記する代わりに、hexadecimalの「h」を最後尾に付けて10hと書くこともあります。また、Javaのプログラミングコード中では数値の接頭辞として「0x」を付けて十六進数を指定しますから、説明文の中でも同じように表記する場合もあります。
コラム
hexadecimal
hexaを調べるとギリシャ語を語源としていて6の意味であることが分かります。するとhexadecimalでなぜ十六進数という意味になるのかよく分からなくなります。この用語が使われるようになった経緯についてはWikipediaのHexadecimalのページ(http://en.wikipedia.org/wiki/Hexadecimal)にいろいろと書いてあります。Wikipediaに書いてあることがすべて正しいとは限りませんが、参考にはなるので紹介しておきます。
以上のことを理解したうえで、次のプログラムを作成してみましょう。まず、十進数の16を出力するに当たり0x10と十六進数表記を使って指定をしてみます。また、0から9までの数値を二進数表記で出力します。これらの値をint型の配列bsへ代入して保持して同じ処理を施します。「b & 0x1」はビット演算を使ってbの1けた目が0か1かを算出しています。「b = b >>> 1」はシフト演算を使って1ビット右へbの値をずらして、bの最上位のビットをゼロで埋めています。これはつまり、bの値が10(2)だったときに「b = b >>> 1」を実行するとbの値は1(2)となるということです。int型は32ビットなので、このシフト演算を32回繰り返し、各けたの値をStringBuffer型の変数sbへ追加します。ただし、この処理でsbをそのまま文字列へ変換すると、表示するときに1けた目の値から順に出力されてしまいます。そこで、「sb.reverse().toString()」とすることにより反転させて文字列へ変換しています。
public class Sample510 {
public static void main(String[] args) {
System.out.println(0x10);
int[] bs = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
for (int j = 0; j < bs.length; j++) {
int b = bs[j];
System.out.print(b+":");
StringBuffer sb = new StringBuffer();
for (int i = 0; i < 32; i++) {
sb.append(b & 0x1);
b = b >>> 1;
}
System.out.println(sb.reverse().toString());
}
}
}
このプログラムの実行結果は次のようになります。確かに「0x10」は「16」と表示されていますし、十進数での0から9までの数値が二進数表記で出力されていることが分かるはずです。
二の補数
さて、ここまでは正の数について説明をしました。次は負の数をどうやって表現しているか確認をしましょう。何度も述べているように、コンピュータは0か1しか使えませんから、例えば「-1」を表すにしても「-」という記号文字を使うことができません。符号も0か1で何とか表現するしかないわけです。そこで、コンピュータの世界では最上位ビットを符号の代わりに使います。最上位ビットが0の場合は正の数、最上位ビットが1の場合は負の数とすると、正の数は変換をすることなくそのまま使えます。
一方、負の数は正の数ほど単純にはいきません。例えばbyte型の場合に「-1(10)」を「10000001(2)」と対応させるのか、「11111111(2)」へ対応させるのか、といったことを決めておく必要があります。これは対応関係を決めればいいだけのことなので、1つ1つの値に対して個別にビット列を対応させて一覧表を作成して、みんなでその一覧表を使って変換するという方法も考えられます。しかし、そんな面倒なことをせずに、簡単に計算できるようになっていた方が明らかに便利です。
そこで、コンピュータの世界ではこの対応を決めるために「二の補数」がよく使われます。計算方法はとても単純で、「正の数を表すビットを反転させて1を加算」するだけです。byte型の-1について具体的に算出してみましょう。「1(10)」は「00000001(2)」ですから、これをビット反転させた「11111110(2)」へ1を加算した結果が「-1(10)」と対応する値になります。これは計算して求めると「11111111(2)」になります。
それではint型についてプログラムを使って確認をしてみましょう。int型が取れる最小値はInteger.MIN_VALUEで定義されているのでこの値を利用します。Integer.MIN_VALUEから(Integer.MIN_VALUE+9)までの値について、各値が二進数のどの値と対応付けられているかを表示してみます。
public class Sample520 {
public static void main(String[] args) {
int bm = Integer.MIN_VALUE;
System.out.println(bm);
for (int j = 0; j < 10; j++) {
int b = bm + j;
System.out.print(b+":");
StringBuffer sb = new StringBuffer();
for (int i = 0; i < 32; i++) {
sb.append(b & 0x1);
b = b >>> 1;
}
System.out.println(sb.reverse().toString());
}
}
}
基本的な動作はSample510クラスと同じですから、特に説明は必要ないでしょう。実行結果から分かることは、Integer.MIN_VALUEは -2147483648(10)であること、-2147483648(10)から-2147483639(10)の各値が順に10000000000000000000000000000000(2)から10000000000000000000000000001001(2)に対応しているということです。
-2147483647(10)の結果を確認してみましょう。2147483647(10)は01111111111111111111111111111111(2)なので、この値の二の補数を求めると、10000000000000000000000000000000(2)へ1(2)を加算したものになります。これはプログラムによって表示された10000000000000000000000000000001(2)に一致していることが分かります。
int型の範囲とまとめ
ここで、int型の範囲について考えてみましょう。言語仕様上は-2147483648(10)から2147483647(10)となっています。なぜこのような範囲になるかというと、32ビットで表現できる整数の数は2の32乗個(4294967296個)あるため、負の数は最上位ビットが1となる値を2147483648個対応させ、ゼロには0を対応させ、正の数は値がそのまま使える残りの二進数2147483647個を使う、というようにしているからです。0の分があるため、正の数の方が1だけ負の数よりも少なくなってしまうのです。
2147483647:01111111111111111111111111111111
2147483646:01111111111111111111111111111110
2147483645:01111111111111111111111111111101
(略)
2:00000000000000000000000000000010
1:00000000000000000000000000000001
0:00000000000000000000000000000000
-1:11111111111111111111111111111111
-2:11111111111111111111111111111110
(略)
-2147483646:10000000000000000000000000000010
-2147483647:10000000000000000000000000000001
-2147483648:10000000000000000000000000000000
さて、実は「二の補数」を使って負の数を表現しておくと、引き算の計算が単純にできてしまいます。次のプログラムで確認をしてみましょう。「-2147483648+2147483647」「-2147483646+2147483646」「-2147483644+2147483645」の計算をしていますから、それぞれ「-1」、「0」、「1」の結果になります。この場合の二進数での計算がどうなっているのかを表示しています。
public class Sample530 {
public static void main(String[] args) {
int bm = Integer.MIN_VALUE;;
int bp = Integer.MAX_VALUE;
for (int j = 0; j < 3; j++) {
int b1 = bm + j * 2;
int b2 = bp - j;
int b3 = b1 + b2;
StringBuffer sb1 = new StringBuffer();
StringBuffer sb2 = new StringBuffer();
StringBuffer sb3 = new StringBuffer();
for (int i = 0; i < 32; i++) {
sb1.append(b1 & 0x1);
sb2.append(b2 & 0x1);
sb3.append(b3 & 0x1);
b1 = b1 >>> 1;
b2 = b2 >>> 1;
b3 = b3 >>> 1;
}
System.out.println(" "+sb1.reverse().toString());
System.out.println("+)"+sb2.reverse().toString());
System.out.println("----------------------------------");
System.out.println(" "+sb3.reverse().toString());
System.out.println("");
}
}
}
結果は次のようになります。「-1」を意味する「11111111111111111111111111111111」、「0」を意味する「00000000000000000000000000000000」、「1」を意味する「00000000000000000000000000000001」が単純な足し算をするだけで求められていることが分かります。ただし、33けた目へ繰り上がった値は破棄されている点には注意してください。
コンピュータの回路設計においては、できるだけ単純な回路だけを使うという要求があります。そういった要求に応えるための1つの工夫として、負の数のデータ表現に二の補数を採用することによって、減算をするための回路を追加せずに、加算をするための回路だけで引き算を実現できるようにしているのです。
ほかの整数型であるbyte型、short型、long型についてもビット長が異なるだけで、これまで解説してきたことが同様に成り立っています。ポイントは、符号付きの整数は二の補数表現を使っていること、その範囲は各型に応じて決められた使用ビット数によって決まるという点です。char型は「Unicode文字表現による16ビット符号なし整数」を値として持つため、整数型ですが負の数はありません。しかし使用可能なUnicodeの範囲は16ビットで表現できる範囲内であるという点は同じです。
Copyright © ITmedia, Inc. All Rights Reserved.

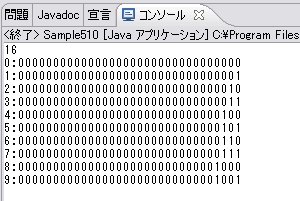 画面1 実行結果
画面1 実行結果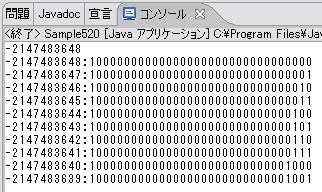 画面2 実行結果
画面2 実行結果 画面3 実行結果
画面3 実行結果



