EclipseでJavaの型を理解する:EclipseでJavaに強くなる(5)(2/3 ページ)
浮動小数点数(Floating Point Type)
■double型とは
数値型のうち基本ともいえる整数型については終わりましたので、次は浮動小数点数について理解しましょう。プログラミング言語Javaのdouble型は「64ビットIEEE 754-1985浮動小数点数(IEEE Standard for Binary Floating-Point Arithmetic(IEEE Standard No.754-1985))」という規格で表現されます。これは小数点を含む数を二進数で表現するものです。ここでは、「64ビットIEEE 754-1985浮動小数点数」の規格の概要について簡単に解説をします。規格の詳細についてはIEEEより資料を手に入れて確認をしてください。
コラム
固定小数点数
世の中には固定小数点数というものもあります。浮動小数点数では小数点の位置が固定されていないのに対して、固定小数点数では固定されています。つまり、整数部分に用いるビット数と小数部分に用いるビット数をあらかじめ固定して表現するものです。
実数を表現するに当たっては、「(符号)(仮数)×(基数)(指数)」と表記する方法があります。例えば、-12は-1.2×101と書くこともできます。この例では、符号が「-」、仮数が「1.2」、基数が「10」、指数が「1」となります。この表記を基にして、「64ビットIEEE 754-1985浮動小数点数」で小数点を含む数を表します。具体的には、最上位の1ビットで符号(sign)、次の11ビットで指数(exponent)、残りの52ビットで仮数(mantissa)を表現しています。指数が格納される部分を指数部、仮数が格納される部分を仮数部といいます。指数部には符号付きの整数値が入ります。仮数部には符号なしの整数値が入ります。
ここで、指数部には符号付きの整数値が入りますが、ここでは二の補数は使われていません。代わりに実際の指数へ1023のバイアス分を足した値を格納することになっています。例えば、「-1乗」の場合は「1022(=-1+1023)」という値が入ることになります。こうしておけば指数部の大小比較が単純にできるようになって便利だからです。
表現できる数には次の5種類があります。指数部と仮数部の値によって意味が変わってくるので注意が必要です。ここで、Infinityは無限大を表す値になります。NaNはNot a Number(非数、数でないもの)という意味になります。
| 種類 | 指数部 | 仮数部 |
|---|---|---|
| ゼロ | 0 | 0 |
| 非正規化数 | 0 | 0以外 |
| 正規化数 | 1..211-2 | 任意の数 |
| Infinity | 211-1 | 0 |
| NaN | 211-1 | 0以外 |
ここで、非正規化数と正規化数という用語が出てきています。仮数部の値は指数部の値(バイアスが足された値)によって、正規化されて格納されているかいないかが判定できます。この指数部の値が「0」より大きく、「2の11乗から2を引いた値」より小さい場合は、仮数部へは正規化された(1を引かれた)小数部の値のみが格納されています。もし指数部の値が「0」なら、仮数部へは正規化をしない値がそのまま格納されています。
プログラムで確認
それでは、doubleが実際にどのようなビット列で表現されているかをSample540クラスを作って調べてみましょう。Sample540クラスのプログラムは長いので、全体は別途次ページに[参考プログラム]として示し、重要なポイントだけ抜粋して説明をします。
文字列で指定された数値を、数値型へ変換するためにはプリミティブ型のラッパークラスにあるparseで始まるメソッドを使います。例えば、Sample540ではdouble型のラッパークラスであるjava.lang.DoubleのparseDoubleメソッドを使っています。
double d = Double.parseDouble(s);
Javaではdoubleは64ビットで表現されています。このビットイメージを同じ64ビットのlong型の変数へコピーするには、java.lang.DoubleのメソッドdoubleToLongBitsを使います。
long l = Double.doubleToLongBits(d);
さらに、これで取得した値を文字列へ変換するためには、long型のラッパークラスであるjava.lang.LongクラスのtoBinaryStringメソッドを使います。ただし、このメソッドを使っただけでは上位ビットの0がすべて省略されてしまうため、補完する必要があります。Sample540クラスではgetBitImageメソッドとしてこれらの処理を提供しています。
String lb = Long.toBinaryString(l);
int longBitLength = lb.length();
for (int i = 64; i > longBitLength; i--) {
lb = "0" + lb;
}
bitImage = lb;
指数部については、実際の値とバイアスされた結果のビットイメージとの両方を表示することができるようにしています。このために、getExponentメソッドとgetExponentBitsメソッドを用意しています。getExponentメソッドでは対象のビット文字列を取り出して、java.lang.LongのvalueOfメソッドを使って2を基数としたビット文字列をLong型の値へ変換し、さらにその値からlongValueメソッドを使ってlongへ変換しています。この値にはバイアスである1023が加算されているので、その値(BIAS)を引いています。なお、BIASはlong型で1023という値であらかじめ宣言されています。getExponentBitsメソッドは対象のビット文字列を取り出しているだけです。
public long getExponent() {
String s = getBitImage().substring(1, 12);
exponent = Long.valueOf(s, 2).longValue() - BIAS;
return exponent;
}
public String getExponentBits() {
String s = getBitImage().substring(1, 12);
return s;
}
仮数部の値を求めるには、指数部の値によって正規化されているかいないかの判断をする必要があります。そこで、Sample540クラスではgetMantissaメソッドを用意して、その処理を行っています。バイアスされた結果の指数部の値が0のとき、getExponentメソッドの値は-BIAS(つまり-1023)となっているので、それを使って判定をしています。指数部については本来の値とバイアスされた値を求めるメソッドを用意していますが、仮数部については本来の値を求めるメソッドだけ用意している点には注意してください。
public String getMantissa() {
if (getExponent() == -BIAS) {
mantissa = "0." + getBitImage().substring(12, 64);
} else {
mantissa = "1." + getBitImage().substring(12, 64);
}
return mantissa;
}
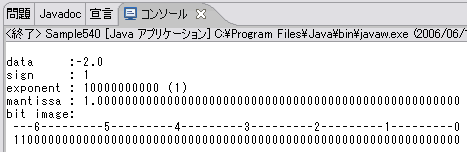
分かりやすい表示をするために、printメソッドを用意してあります。また動作を確認するためにmainメソッドを用意し、1.0、2.0、1024.0、118.625などの結果を正負それぞれについて計算して出力しています。ここでは確認のために単純な-2.0と1024.0の結果を見てみましょう。
まず-2.0ですが、符号は負なので「1」となります。指数部は「1」なので、バイアスの1023(10)(01111111111(2))を加えて「10000000000(2)(1024(10))」となります。仮数部は正規化される(1を引かれる)ので、ビットイメージでは0となります。
次に1000.0ですが、符号は正なので「0」となります。1000.0(10)は1111101000(2)なので、1.111101×29となります。つまり指数部は「9(10)(1001(2))」となります。バイアスの1023(10)(01111111111(2))を加えて「10000001000(2)(1032(10))」となります。仮数部は正規化される(1を引かれる)ので、ビットイメージでは小数部の「111101」の後ろへ仮数部の長さが52になるまで「0」で埋めた値が入ります。
どうでしょう、こうやっていろいろな数値がビット列で表現できるというのは興味深いのではないでしょうか。ところで、Infinity、NaNはどんなときに出力されるのでしょうか。例としては、1.0を0.0で割った値と0.0を0.0で割った値があります。これも試しにプログラムで出力してみましょう。
public class Sample550 {
public static void main(String[] args) {
double a = 1.0;
double b = 0.0;
double c = 0.0;
System.out.println(a/b);
System.out.println(b/c);
}
}
実行結果は次のようになります。
Copyright © ITmedia, Inc. All Rights Reserved.


 画面4 実行結果
画面4 実行結果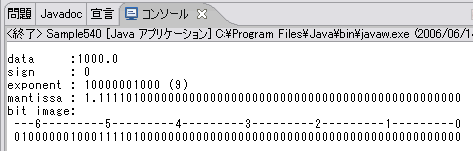 画面5 実行結果
画面5 実行結果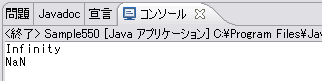 画面6 実行結果
画面6 実行結果



