Firebugで探索アルゴリズムを見ていこう：コーディングに役立つ！ アルゴリズムの基本（6）（4/4 ページ）

[山下寛人，オイシックス株式会社]

計算量を考える

　いままでいろいろなアルゴリズムを見てきました。パフォーマンスが悪いもの、良いものいろいろありました。パフォーマンスの良しあしを考えるときに、計算量という考え方があります。アルゴリズムがどれくらいのパフォーマンスなのかをある程度予測することができます。

　計算量には時間計算量と領域計算量があります。領域計算量はメモリやディスクなどの領域をどれくらい使うかということです。時間計算量は実行に要する時間です。

　計算量がどれくらいかを表す際にはO-記法を用います。O（オー）はオーダー（order）の頭文字です。O(1)やO(n)と表します。

　例えば以下のようなプログラムがあります。

a = b + c;

　1回だけ計算を行うプログラムです。この場合、「時間計算量のオーダーはO(1)である」と表現します。

　以下のプログラムの時間計算量のオーダーはO(n)です。n回処理を繰り返しているからです。

for (i = 0; i < n; i++) { }

　また、次のプログラムの時間計算量のオーダーもO(n)です。

for (i = 0; i < n; i++) { a = b + c; }

　計算量のオーダーは何に比例するかに着目します。forループの中にO(1)の処理があっても全体として計算量はnに比例します。従って計算量のオーダーはO(n)になります。

　次の例の計算量のオーダーはO(n^2)となります。

for (i = 0; i < n; i++) {
   for (j = 0; j < n; j++) {
   }
}

逐次探索の時間計算量

　逐次探索の時間計算量を考えてみましょう。

　ループの回数に着目します。探索対象のデータの個数が128個のとき、たまたま最初のデータが目的のものだったらループは1回です。運悪く最後のデータだった場合は128回目のループでやっと探索成功になります。平均すると64回のループで目的のデータを見つけることができそうです。

　データの個数をn個とすると、n/2回のループということになります。n/2はnに比例しますので、逐次探索の時間計算量のオーダーはO(n)になります。

二分探索の時間計算量

　では二分探索ではどうでしょう。1回目のループで対象を半分の64個に絞り込みます。2回目のループで32個。3回目のループで16個。4回目のループで8個。途中省略して7回目のループで1個に絞り込まれます。128は、2の7乗です。

　データの個数をnとして、ループ回数をmとすると、nは2のm乗という関係があります。こういう数は数学では対数と呼びましたね。m=log nと表します。正確にはlog₂ n ですが、計算量を表すときは2を省略することが多いです。

　ループ回数がlog nなので、二分探索の時間計算量のオーダーはO(log n)になります。

選択ソートの時間計算量

　選択ソートの時間計算量はどうなるでしょうか（選択ソートの詳細は第4回「Internet Explorerよりも速くソートできるかな」をご覧ください）。

　要素の数がn個の場合、ループ回数は(n-1)+(n-2)+…2+1となります。この式を書き直すと、n*(n-1)/2 = (n^2)/2-n/2と表せます。この式の中でnが大きくなっていくと最も大きくなっていくのはn^2の部分です。従って選択ソートの時間計算量のオーダーはO(n^2)になります。

ハッシュテーブル

　探索アルゴリズムに戻ります。ここまでは探索対象のデータを配列に保持しました。配列ではなくより探索に適したデータ構造はないでしょうか。そこでハッシュテーブルというアルゴリズムを紹介しましょう。

　あるキーに対応するデータを保持する場合、最も簡単な方法はデータのアドレスを直接キーに対応させる方法でしょう。メモリやディスク上で、データを保存する先頭アドレスを決め、そこから先に一定間隔でデータを保持していけば、あるキー値に対応するアドレスは先頭アドレス＋キー値×1件のデータ容量で求められます。あるいは配列にするなら配列のインデックスをそのままキー値とすればよいでしょう。

　この方法の問題は、キー値によっては非常にたくさんのデータ容量を必要とすることです。キー値が10000のデータがある場合は、1から9999までのデータがなくてもその分の領域は無駄に空けておかないといけません。

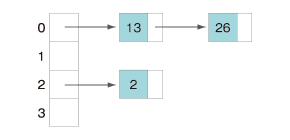
　そこで、キー値を一定の法則で変換してある範囲の値に収まるようにします。よくあるやり方は、一定の数値で割って余りを使う方法です。例えば13で割った余りにすれば値の範囲は0から12の間になります。この変換をハッシュ、変換した結果をハッシュ値と呼びます。

　このハッシュ値の位置にデータを保管します。こうした場合、また別の問題が発生します。ハッシュ値が重複する場合があります。13で割った余りだと、キー値13もキー値26もハッシュ値は0となり重複してしまいます。そこでそれぞれのハッシュ値の中に複数のデータを保持できるようにします。例えばリスト構造にしておきます。

　値を探索する場合は、キー値からハッシュ値を求めます。そのハッシュ値に対応するリストを取得します。そのリストを順にたどってキー値に一致するデータを取得します。

ハッシュテーブルのソースコード

　次のソースコードを二分探索のコードの最後、「末尾2」のコメントの下に追加します。

<div id="hash">ハッシュテーブル<br></div><hr>
<script type="text/javascript">
function HashTable(ary) {
  //this.table = new Array(997);
  this.table = new Array(4);
  for (var i = 0; i < ary.length; i++) {
    var item = ary[i];
    this.push_hash(item.key, item.value);
  } 
}
 
HashTable.prototype.toString = function() {
  var str = "{";
  for (var i = 0; i < this.table.length; i++) {
    if (this.table[i] === undefined) { continue; }
    if(2 <= str.length) { str += ","; }
    str += i + "=>" + this.table[i];
  }
  str += "}";
  return str;
} 
 
HashTable.prototype.display = Array.prototype.display;
 
Number.prototype.calcHashCode = function(len) {
  return (this % len);
}
 
HashTable.prototype.push_hash = function(key, value) {
  var hash_code = key.calcHashCode(this.table.length);
  if (this.table[hash_code] === undefined) {
    this.table[hash_code] = [];
  }
  this.table[hash_code].pushItem(key, value);
  this.view_id = "hash";
}
 
HashTable.prototype.search = function(key) {
  var hash_code = key.calcHashCode(this.table.length);
  var list = this.table[hash_code];
 
  if (list === undefined) { return null; }
  for (var i = 0; i < list.length; i++) {
    if (list[i].key == key) { return list[i].value; }
  } 
  return null;
}
 
var hash = new HashTable(array.clone());
hash.view_id = "hash";
hash.display(hash);
hash.display("find: " + hash.search(5));
</script>

　ソースコードを解説します。

3〜10行目

ハッシュテーブルとそのコンストラクタです。配列を基にそれぞれの配列の要素をハッシュテーブルに追加します。

今回はアルゴリズムを分かりやすくするため5行目でハッシュテーブルの要素数を4にしています。一般的に割り算の分母は素数にしておいた方が均等に分かれます。4行目はコメントアウトしてありますが、997は1000以下の最大の素数なので、実際にはこういった数を使った方がよいでしょう。

12〜21行目

ハッシュテーブルの中身を文字列で表示する関数です。

25〜27行目

数値のハッシュコードを求める関数です。数値そのものに関数を追加していることに注意しましょう。JavaScriptに特有の記述法です。StringにcalcHashCode関数を定義すればキーに文字列を使うこともできるようになります。

29〜36行目

ハッシュにデータを追加する関数です。ハッシュ値を求め、ハッシュコードに対応する配列の要素を取得します。これがリストになっていて、そのリストにデータを追加します。

38〜47行目

ハッシュからデータを探索する関数です。キー値からハッシュ値を求め、それに対応するリストを取得します。そのリストのキー値を順に調べ、一致したら値を返します。

デバッガでハッシュテーブルを見る

　次の2行にブレークポイントを設定しましょう。

var list = this.table[hash_code];
if (list[i].key == key) { return list[i].value; }

　Firefoxをリロードすると、thisにハッシュテーブルができているのが分かります。keyが5、hash_codeが1になっています。

　再開ボタンをクリックすると、listという変数が出てきます。これがハッシュ値1に格納されているリストです。iの値に対応するデータは、キー値1で5と一致しません。従ってループが続きます。

　また再開ボタンをクリックすると、iの値が1に変わります。iの値に対応するデータはキー値5なので一致します。これで関数の実行は終了するはずです。

　もう一度再開ボタンをクリックすると最後まで実行されて処理が終了します。

　ここまでさまざまな探索アルゴリズムを紹介してきました。ほかにも木構造を使った探索アルゴリズムもありますので、興味があれば調べてみてください。次回は文字列検索アルゴリズムを紹介します。

著者紹介

山下 寛人

オイシックス株式会社

「次回」へ

「コーディングに役立つ！ アルゴリズムの基本」バックナンバー

• レコメンデーションとエディットグラフ
• データを加工して圧縮率を高めよう
• データ量を操る圧縮／展開を究めよう
• 文字列の中から効率良くキーワードを探し出せ
• Firebugで探索アルゴリズムを見ていこう
• Internet Explorerよりも速くソートできたよ
• Internet Explorerよりも速くソートできるかな
• 再帰でハノイの塔を攻略せよ
• データ構造の選択次第で天国と地獄の差
• いまさらアルゴリズムを学ぶ意味