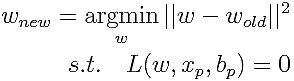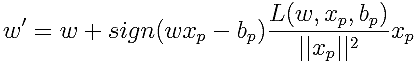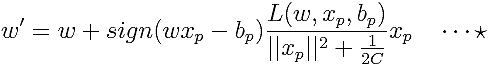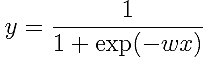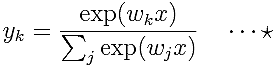Hadoopによるテキストマイニングの精度を上げる2つのアルゴリズム:テキストマイニングで始める実践Hadoop活用(最終回)(2/3 ページ)
Passive-Aggressiveの重みの更新
前回は、青空文庫の作品を1つずつ見ていって、新しいデータの損失を小さくするような方向にだんだんと“重み”を更新していきました。
しかし、Passive-Aggressiveは、「新しいデータの損失が必ずゼロであるように重みを更新する」のが特徴です。先ほどの例だと、寿命の予測値が55歳から57歳になるような重みに更新するということです。
PassiveとAggressiveの違い
損失がゼロであるように新しく重みを更新するということは、新しいデータに対してすでに損失がゼロの場合には、重みを更新しません。新しいデータに対し、「55.5歳」などと予測した場合は「重みは、そのまま」ということです。これが、Passive-Aggressiveの「Passive」です。
損失がゼロでない場合のみ、損失がゼロであるような新しい重みに更新します。これが「Aggressive」です。
新しいデータに対し、60歳などと外れた値を予測した場合に、55〜57歳の値を予測するように重みを更新するということです。しかし、そのように55〜57歳の値を予測する重みは、たくさん考えられます。
Passive-Aggressiveを数式で表すと
Passive-Aggressiveでは、そのような重みの中から、古い重みに最も近いものを選びます。このことを数式で表してみます。
「||」で囲まれているのはベクトルの長さで、wと
(古い重み)の距離の2乗を表しています。
は、「wと
の距離が最小となるようなwを求める」ということで、これを新しい重み
として更新します。
「s.t.」とは、制約条件という意味で、wは「損失がゼロになるという条件」という意味です。その条件の下で、wと
の距離が最小となるようなwを計算して、更新するのです。
つまり、新しいデータの損失がゼロ、正しく推定するような新しい重みの中で、古い重みに最も近いものを計算するということです。先ほどの例でいうと、55〜57歳を予測するような重みはたくさん考えられますが、その中で古い重みに最も近いものを選択します。
前回のように、新しいデータの損失が小さくなるような方向にだんだんと重みを更新するのではなく、新しいデータの損失が必ずゼロになり、かつ古い重みに最も近いものにガツッと更新するイメージです。この数式を計算すると、以下のように重みを更新していけばいいことになります。
「sign」は「カッコ内の符号」という意味で、
は先ほどの損失関数に値を代入したものです。前回作成したプログラムを少し変更するだけで、重みを更新できるのが分かると思います。
「PA-II」(Passive-Aggressive II)とは
なお、Passive-Aggressiveは、新しいデータを必ず正しく推定するように重みを更新するため、正解が間違っているデータが少しでも含まれていた場合に悪影響を受けてしまうなどの欠点があります。そこで、重みの更新を和らげる「PA-II」(Passive-Aggressive II)という方法があります。
Cは任意の数で、この値が小さければ小さいほど、重みの更新を和らげる役割です。今回は、このPA-IIを使ってMapReduceプログラムを作成していきましょう。
Passive-AggressiveのMapReduceプログラムの作成
Passive-AggressiveのMapReduceプログラムを作成していきましょう。とはいっても、前回のプログラムから変更する部分はあまりありません。前回のLeastSquaresMapperを継承した、PassiveAggressiveMapperクラスを作ります。
1 public class PassiveAggressiveMapper extends LeastSquaresMapper {
2 private double genErr = 1; // e
3 private double penalty = 0.01; // C
4
5 @Override
6 public void setup(Context context) throws IOException, InterruptedException {
7 Configuration conf = context.getConfiguration();
8 genErr = conf.getFloat("generalization.error.size", (float) genErr);
9 penalty = conf.getFloat("penalty.size", (float) penalty);
10 super.setup(context);
11 }
12
13 @Override
14 public void map(VIntWritable key, MapWritable value, Context context)
15 throws IOException, InterruptedException {
16 int b = key.get();
17 value.put(new Text(CommonUtil.BIAS_KEY), new VIntWritable(1));
18 double wx = DiscriminantFunctionAlgorithm.predict(value, weightMap);
19 int squareNormX = 0;
20 for (Entry<Writable, Writable> entry : value.entrySet()) {
21 int x = ((VIntWritable) entry.getValue()).get();
22 squareNormX += x * x;
23 }
24 for (Entry<Writable, Writable> entry : value.entrySet()) {
25 Text word = (Text) entry.getKey();
26 int x = ((VIntWritable) entry.getValue()).get();
27 DoubleWritable weightWritable = (DoubleWritable) weightMap.get(word);
28 double diffWeight = Math.signum(b - wx)
29 * Math.max(0, Math.abs(wx - b) - genErr)
30 / (squareNormX + 1 / 2 / penalty) * x;
31 if (weightWritable == null) {
32 weightMap.put(word, new DoubleWritable(diffWeight));
33 } else {
34 double w = weightWritable.get() + diffWeight;
35 weightWritable.set(w);
36 }
37 }
38 }
39 }
LeastSquaresMapperから変更があった部分を強調してあります。8?9行目では、Passive-Aggressiveのパラメータ、
C
を読み込んでいます。19〜23行目では、
を計算しています。28〜30行目で、Passive-Aggressiveで更新する重みの差分を計算しています。他は、LeastSquaresMapperと同じです。
実行
前回作成した、IterativeParameterMixingDriverのsetMapperClass関数の引数を以下に変更すれば、実行できます。
job.setMapperClass(PassiveAggressiveMapper.class);
予測もまったく同じプログラムで可能です。再び記事「モテる女子力を磨くための4つの心得「オムライスを食べられない女をアピールせよ」等 - Be Wise Be Happy Pouch [ポーチ]」のテキストから作者の寿命を予測してみましょう。
あなたは51.030671894504216歳で死ぬでしょう。
よりPassive-Aggressiveについて知りたい場合には
より、Passive-Aggressiveについて知りたい場合は以下のサイトや論文が参考になります。
Passive-Aggressiveについて、今回の記事で紹介した数式の導出も含めて、詳しく解説しています。
Passive-Aggressiveについて分かりやすく解説した記事です。他にもブログには機械学習やテキストマイニングなどの役立つ記事が数多くあります。
Passive-Aggressiveの元論文です。
Gmailの優先トレイに関する論文です。
確率を推定する「ロジスティック回帰」とは
次に、ロジスティック回帰という手法を紹介します。冒頭で述べたように、ロジスティック回帰は、分類に使われるアルゴリズムです。例えば、メールのスパムフィルタリング処理で、メールを「スパム」「スパムでない」の2つのカテゴリに分類するといった用途で使います。
今回は、寿命を10〜14歳、15〜19歳、20〜24歳などにカテゴリに分けて、どのカテゴリに属するか推定してみることにしましょう。
なぜ「回帰」?
そもそも、分類に使われるのに、なぜロジスティック「回帰」という名前が付いているのでしょうか? 今までは、寿命のような数値を推定していましたが、ロジスティック回帰では、「確率」を推定します。
例えば、メールの文章から、「スパム」のカテゴリに属する確率を推定します。「0.9」と推定されたら「スパムでない」カテゴリよりも「スパム」カテゴリに属する確率が高いので、「スパム」カテゴリに分類するといった具合です。
回帰で確率を推定できるので、カテゴリに属する確率を考えることで分類問題として使えます。
ただし、単純に今までのようにどんな数値を推定してもいいというわけではありません。確率を推定するということですので、0〜1の間の値を取るように工夫がされています。
ロジスティック回帰を数式で表すと
今までは、以下のように重みベクトルとデータのベクトルを掛けて、寿命の数値を予測していました。
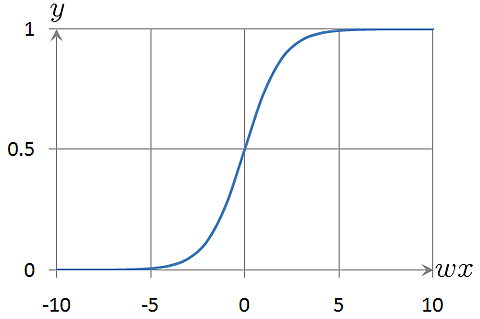
しかし、ロジスティック回帰では、以下のような式で確率を予測します。
この式をグラフで表してみます。
予測結果yが0?1の間の確率の形になっているのが、分かると思います。
カテゴリが3個以上になると
なお、上の式はカテゴリが2つの場合です。カテゴリが2つの場合は、あるカテゴリに属する確率を1つだけ計算すれば、どのカテゴリに属するかを判別できます。しかし、今回は寿命を10〜14歳、15〜19歳、20〜24歳など複数のカテゴリに分けるので、カテゴリの数だけ確率の推定が必要になります。推定した複数のカテゴリの確率の中で、最も確率が高いカテゴリに分類するのです。
それぞれのカテゴリに対し、複数の確率を予測するので、カテゴリごとの重みを考えます。
それぞれカテゴリごとの確率を予測してみましょう。カテゴリ「k」の確率を予測する式は以下の通りです。
カテゴリ「k」の重みが
です。分母は、すべてのカテゴリに対して、「exp(wx)」を計算したものの総和です。
「もっともらしさ」を表す「尤度関数」とは
今までは損失関数を定義して、その損失をなるべく小さく、あるいはゼロにするように重みを更新していきました。今回も同じく損失関数の損失をなるべく小さくするようにだんだんと重みを更新します。しかし、その前に「尤度関数(ゆうどかんすう)」というものを考える必要があります。
青空文庫の各作品を、以下とします。
例えば、ある作品の著者の寿命が63歳だとすると、属するカテゴリは60〜64歳です。このカテゴリ、つまり正解のカテゴリに属する確率を推定してみます。
10〜14歳、15〜19歳……といったカテゴリごとの確率を推定するには、先ほどの式
をそれぞれ計算すればいいのでした。その中でも、正解のカテゴリである60歳〜64歳に属する確率を計算すればいいわけです。
この「正解のカテゴリに属する確率」の推定結果を作品ごとに並べます。
もちろん、作品ごとに正解のカテゴリは違うわけですので、ぞれぞれ別々の重みで
を計算します。この確率の推定結果を掛け合わせてみましょう。
これは何を意味しているのでしょうか。正解のカテゴリに属する確率が大きければ、その正解のカテゴリに分類されますので、大きければ大きいほど良いといえます。
つまり、「正解のカテゴリに属する確率の推定結果を掛け合わせたこの関数は、できるだけ大きい方が良い」ということになります。この関数を尤度関数といいます。
尤度関数はカテゴリごとの重み
の関数であることに注意してください。尤度関数をできるだけ大きくするように重み
を推定すれば、正解の寿命に即した確率を返せるようになるわけです。
次ページでは、尤度関数がなるべく大きくなるような重みを求めていく方法を考えてみます。その後、ロジスティック回帰のMapReduceプログラムを作成し実行してみましょう。
Copyright © ITmedia, Inc. All Rights Reserved.