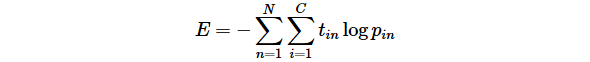第5回 画像認識を行う深層学習(CNN)を作成してみよう(TensorFlow編):TensorFlow入門(1/2 ページ)
ディープラーニングの代表的手法「CNN」により画像認識を行う機械学習モデルを構築してみる。CNNによる深層学習がどのようなものか体験しよう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
ご注意:本記事は、@IT/Deep Insider編集部(デジタルアドバンテージ社)が「deepinsider.jp」というサイトから、内容を改変することなく、そのまま「@IT」へと転載したものです。このため用字用語の統一ルールなどは@ITのそれとは一致しません。あらかじめご了承ください。
前回はCNNの全体像を説明したので、本稿の手順で作業を始める前に一読してほしい。CNNの全体像が分かったところで、今回はいよいよCNNを使って深層学習を試してみよう。本稿のPythonコードは、Jupyter Notebook上で実行すればよい。
CNNの学習
試すといっても、具体的に画像データセットから学習してモデルを作成し、新しいデータを与えたときに判別してくれるのでなければ意味がない。本節では、MNISTと呼ばれる手書き数字画像のデータセットを用いて学習を行う。すなわち、そのモデルを利用することで、新しい手書き数字画像を得たときに、その画像に記されている数字が何であるかを判別できるようにしてみよう。
MNISTデータの取得
MNISTでは以下の4種類のファイルを配布している。
| ファイル名 | 用途 | 内容 | データ数 |
|---|---|---|---|
| train-images-idx3-ubyte.gz | 訓練 | 画像データ | 60,000 |
| train-labels-idx1-ubyte.gz | 訓練 | ラベル | 60,000 |
| t10k-images-idx3-ubyte.gz | テスト | 画像データ | 10,000 |
| t10k-labels-idx1-ubyte.gz | テスト | ラベル | 10,000 |
| 表1 MNISTの4種類のファイル | |||
画像データには、0〜9のいずれかの手書き数字が記されている、28×28ピクセルのグレースケールの画像で、各ピクセルは8 bitsの単一の値をとる。MNISTのページに詳細なファイルの仕様が記述されている。仕様に従い読み込んでもよいのだが、MNISTはよく利用されるデータなので、TensorFlowにもチュートリアルとして、データを読み込む関数があらかじめ用意されている。本稿ではこれを利用する(リスト1)。
from tensorflow.examples.tutorials.mnist import input_data
# MNIST_dataディレクトリーにMNISTデータをダウンロードして読み込む
mnist = input_data.read_data_sets('MNIST_data/')
作成した変数mnistには、mnist.train、mnist.validation、mnist.testの3つのデータが含まれる。mnist.trainとmnist.validationは6万個の訓練用データを5万5000個と5000個に分割したもので、mnist.testは1万個のテスト(test)用データだ。
機械学習においてモデルを作成する際には、モデルを作成するのに使ったデータを使って精度を測ると上振れしてしまう(過学習という)。これを防ぐために、精度検証(validation)用に訓練(train)用データの一部を取り出すのが普通であり、チュートリアルの関数でもそのようになっているというわけである。ただし、精度検証データは使わず、テストデータで精度検証を済ませる場合もある。本稿でも精度検証データは使用しない。
mnist.XXX.imagesには、MNISTの数字画像データ(テンソル)が含まれている。テンソルのサイズはデータ数×784の行列形式で、例えばmnist.train.imagesは55000×784のサイズである。784は28×28で、2次元のピクセルデータが1次元に直列に配置されている。
また、mnist.XXX.labelsには数字のラベル(画像が示す数字が何であるか)が含まれている。
例として1つ目の画像を出力してみよう。実行にはまず、画像データを扱うためのpillowパッケージをターミナル上から導入する(リスト2)。
(introtensorflow) $ pip install pillow
インストールが完了したら、リスト1のコードに続けて、リスト3のコードをJupyter Notebook上で実行してみよう。
# pip install pillow
from PIL import Image
# 1枚目を28×28ピクセルの行列に変換
image_matrix = tf.reshape(mnist.train.images[0], [28, 28])
# 画像を8 bits整数値行列に変換する
image_matrix_uint8 = tf.cast(255 * image_matrix, tf.uint8)
# ラベルの表示
print(mnist.train.labels[0])
# グレースケール画像データの作成
Image.fromarray(image_matrix_uint8.eval(), 'L')
すると、図1のような結果が表示されるはずだ。これが1つ目の訓練データのラベルと画像である。
筆者には3に見えるが、付けられているラベルは3ではなく7である。英語圏では7の真ん中に横線を入れる書き方が一般的だ。
ネットワークの定義
本稿では説明のために、精度は追求せずに、以下の単純なCNN構造を定義する。
| レイヤー | 処理 | メソッド | 入力サイズ | 出力サイズ | 処理詳細 |
|---|---|---|---|---|---|
| (1) | サイズ変更 | tf.nn.reshape | 784 | 28×28 | 畳み込みのための変形 |
| (2) | 畳み込み | tf.nn.conv2d | 28×28 | 9×9×10 | ランダム生成したサイズ4×4のカーネル、ストライド幅3で10個適用 |
| (3) | 活性化関数 | tf.nn.relu | 9×9×10 | 9×9×10 | ReLU関数 |
| (4) | プーリング | tf.nn.max_pool | 9×9×10 | 4×4×10 | ウィンドウサイズ3×3、ストライド幅2で最大値プーリング |
| (5) | サイズ変更 | tf.reshape | 4×4×10 | 160 | 全結合のための変形 |
| (6) | 全結合 | tf.matmul | 160 | 40 | |
| (7) | 活性化関数 | tf.nn.relu | 40 | 40 | ReLU関数 |
| (8) | 全結合 | tf.matmul | 40 | 10 | |
| (9) | 確率化 | tf.nn.softmax | 10 | 10 | ソフトマックス関数 |
| 表2 本稿で用いるCNNのレイヤー構造 | |||||
活性化関数のReLU関数(正規化線形関数:Rectified Linear Unitの略)のみ初出なので補足を加える。ReLU関数は以下の式で定義される関数で、入力が0以下であれば0とし、入力が0より大きければ入力通りとする。
ReLU関数は、ニューラルネットワークを収束させる上で都合がよい性質(具体的には図2に示すように、 x=0 で折れ曲がる構造)を持っており、深層学習によく用いられる。
損失関数の定義
損失関数は、理想的な出力との距離を定義する関数だ。数学的に厳密に定義された距離である必要はないが、距離の値が小さいほど「理想的な出力に近い」と判断できるように定義する必要がある。この関数の値が小さくなるように、TensorFlowがパラメーターを調整する。
上記で定義したネットワークの出力は、10要素からなるテンソルだ。もし、ある数字の画像から「0〜9の数字」を判断するときに、各数字である確率が完全に等しければ、[0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]という出力を得ることになり、これでは確率値から正解は判断できない。これは、理想的な出力との距離が遠い、つまり損失関数の値が大きすぎる状態である。
正解の数字をより正確に判断できるようにするには、例えば3が正解の場合、どのような出力であることが理想だろうか。確率から出力を判断するとは、確率が最大であるものを選択するということであるから、[0, 0, 0, 1, 0, 0, 0, 0, 0, 0]のように3を示す要素が1で他の要素が0である場合が、最も良い出力であるといえよう。このような出力になるように、つまり損失関数の値が最小になるようにパラメーターを最適化していく必要があるわけだ。
ちなみに、このような正解の要素のみ1で他の要素が0となるテンソル表現をワンホット表現(One-hot representation)と呼び、損失関数の定義に便利である。後でコードで示すが、MNISTのチュートリアルデータの読み込み時に、ラベルをワンホット表現として読み込むこともできる。
詳細は説明しないが、MNISTのような判別問題では、以下の交差エントロピー(cross entropy)と呼ばれる損失関数がよく用いられる。
Ν は学習に利用した画像の枚数、 C は判別クラス数(MNISTの場合は10)、 tin はワンホット表現(正解ラベル)の i 番目の要素、 pin はネットワークの出力の i 番目の要素を表す。
定義に従えば、TensorFlowでは、以下のように交差エントロピーを計算できる。
y = tf.nn.softmax(x)
entropy = -tf.reduce_sum(t * tf.log(y))
※xやtは現段階では未定義なので、このコードは実行できない。実際の実行例はリスト6を参照。
ソフトマックス関数と交差エントロピーの組み合わせはよく利用されるので、上記の処理は次のようにまとめることもできる。
entropy = tf.nn.softmax_cross_entropy_with_logits_v2(labels=t, logits=x)
※tやxは現段階では未定義なので、このコードは実行できない。実際の実行例はリスト6を参照。
損失関数を最小化するのが、オプティマイザー(optimizer)と呼ばれる最適化手法を実装したクラス群だ。本稿では説明を行わないが、損失関数を最小化するために、損失関数とセットで現れるものだと思っておいて間違いない。TensorFlowでは、オプティマイザーを評価することで学習を進めることができる。
オプティマイザーにもさまざまな種類があるが、ここではAdam(tf.train.AdamOptimizerクラス)という手法を利用する。利用方法は次節のリスト6を参考にしてほしい。
学習の実行
リスト6に、MNISTの訓練データを用いた学習の実行と、(今回は精度検証データではなく)テストデータを用いた精度推定を行うコードを示す。一部のテンソルに対してname引数で名前を付けているが、この理由は後で説明する。
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
sess = tf.InteractiveSession()
# 再現性の確保のために乱数シードを固定(数値は何でもよい)
tf.set_random_seed(12345)
# 入力データ
# MNISTのワンホット表現での読み込み
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# (0) 入力画像
x = tf.placeholder(tf.float32, name='x')
# (1) サイズ変更
x_1 = tf.reshape(x, [-1, 28, 28, 1])
# (2) 畳み込み
# ランダムカーネル
k_0 = tf.Variable(tf.truncated_normal([4, 4, 1, 10], mean=0.0, stddev=0.1))
# 畳み込み
x_2 = tf.nn.conv2d(x_1, k_0, strides=[1, 3, 3, 1], padding='VALID')
# (3) 活性化関数
x_3 = tf.nn.relu(x_2)
# (4) プーリング
x_4 = tf.nn.max_pool(x_3, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID')
# (5) サイズ変更
x_5 = tf.reshape(x_4, [-1, 160])
# (6) 全結合
# 重みとバイアス
w_1 = tf.Variable(tf.zeros([160, 40]))
b_1 = tf.Variable([0.1] * 40)
# 全結合
x_6 = tf.matmul(x_5, w_1) + b_1
# (7) 活性化関数
x_7 = tf.nn.relu(x_6)
# (8) 全結合
# 重みとバイアス
w_2 = tf.Variable(tf.zeros([40, 10]))
b_2 = tf.Variable([0.1] * 10)
# 全結合
x_8 = tf.matmul(x_7, w_2) + b_2
# (9) 確率化
y = tf.nn.softmax(x_8)
# (10) 損失関数の最小化
# 正解ラベル
labels = tf.placeholder(tf.float32, name='labels')
# 損失関数(交差エントロピー)と最適化処理(Adam)
loss = -tf.reduce_sum(labels * tf.log(y))
optimizer = tf.train.AdamOptimizer().minimize(loss)
# (11) 精度検証
prediction_match = tf.equal(tf.argmax(y, axis=1), tf.argmax(labels, axis=1))
accuracy = tf.reduce_mean(tf.cast(prediction_match, tf.float32), name='accuracy')
# パラメーター
# バッチサイズ
BATCH_SIZE = 32
# 学習回数
NUM_TRAIN = 10_000
# 学習中の出力頻度
OUTPUT_BY = 500
# 学習の実行
sess.run(tf.global_variables_initializer())
for i in range(NUM_TRAIN):
batch = mnist.train.next_batch(BATCH_SIZE)
inout = {x: batch[0], labels: batch[1]}
if i % OUTPUT_BY == 0:
train_accuracy = accuracy.eval(feed_dict=inout)
print('step {:d}, accuracy {:.2f}'.format(i, train_accuracy))
optimizer.run(feed_dict=inout)
# テストデータによる精度検証
test_accuracy = accuracy.eval(feed_dict={x: mnist.test.images, labels: mnist.test.labels})
print('test accuracy {:.2f}'.format(test_accuracy))
実行してみると、恐らく35%前後の精度となるだろう。これは、数字画像が与えられたときにその数字を当てられるのが、およそ3回に1回程度ということだ。これでは使い物にならない。精度を上げるための工夫が必要になる。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


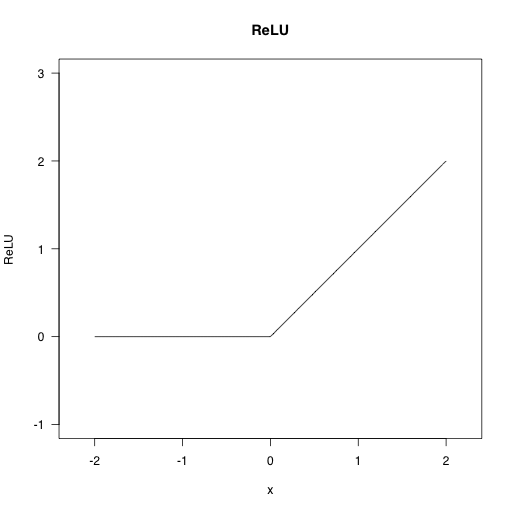 図2 ReLU関数
図2 ReLU関数