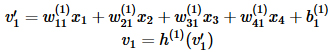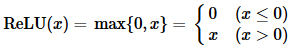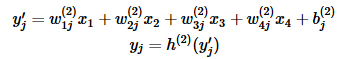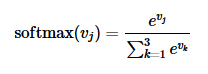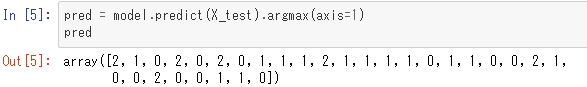ニューラルネットワークライブラリTensorFlow／Kerasで実践するディープラーニング：Pythonで始める機械学習入門（8）（1/3 ページ）

最近流行の機械学習／Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ／ツールの使い方を中心に解説する連載。今回はニューラルネットワークのライブラリであるTensorFlow／Kerasについて解説します。

[加藤公一，シルバーエッグ・テクノロジー]

　プログラミング言語「Python」は機械学習の分野で広く使われており、最近の機械学習／Deep Learningの流行により使う人が増えているかと思います。一方で、「機械学習に興味を持ったので自分でも試してみたいけど、どこから手を付けていいのか」という話もよく聞きます。本連載「Pythonで始める機械学習入門」では、そのような人をターゲットに、Pythonを使った機械学習について主要なライブラリ／ツールの使い方を中心に解説しています。

　連載第1回の「Pythonで機械学習／Deep Learningを始めるなら知っておきたいライブラリ／ツール7選」では、ライブラリ／ツール群の概要を説明しました。連載第3回から第1回で紹介した各種ライブラリを使う具体的なコードを例示していますが、Jupyter Notebook形式で書いています。

　今回はニューラルネットワークのライブラリである「TensorFlow」について解説します（注）。TensorFlowそのものではなく、その上部で動作するライブラリ「Keras」を使います。

注：TensorFlowは、ニューラルネットワークに限らず、さまざまな最適化問題に適用できますが、特にニューラルネットワークの実装によく使われています。

　使い方を理解するにはある程度アルゴリズムの仕組みについての理解が必要なので、まずはアルゴリズムについて説明します。ここで説明するのは、以降のサンプルプログラムを理解するための最小限のものです。

　なお本稿では、Pythonのバージョンは3.x系であるとします。

※今回のサンプルコードは、こちらからダウンロードできます

ニューラルネットワークの基本

　まずはTensorFlowの説明の前に、ニューラルネットワークについて説明します。「ディープラーニング（深層学習）」と呼ばれるアルゴリズムが画像の分類でブレークスルーを起こしたことで脚光を浴びました。ニューラルネットワークとは、このディープラーニングを包含するアルゴリズムの名称です。

あやめデータを例に見るニューラルネットワーク、ディープラーニングの仕組み

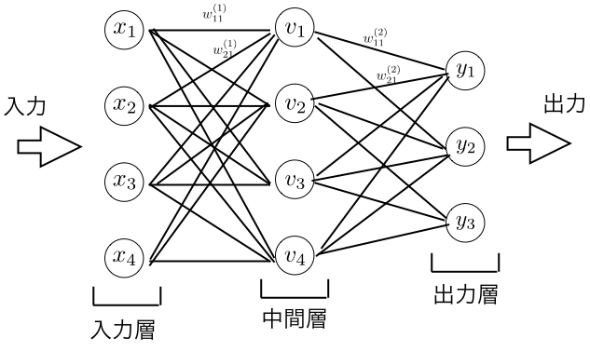
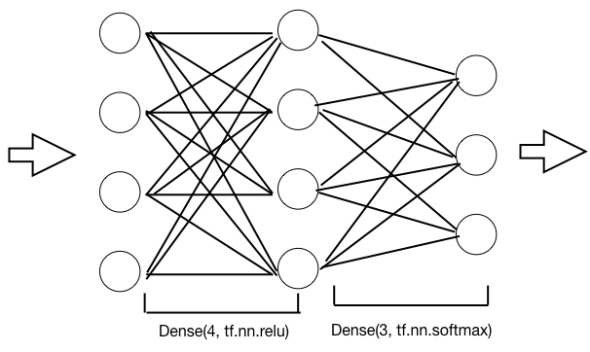
　アルゴリズムの説明のため、簡単な例を使って説明します。ここでは、前回の記事でも利用したあやめの分類に適用してみます。あやめの特徴量は4種類あるので、入力として4つの値が与えられます。ニューラルネットワークのアルゴリズムは次のような図で説明されます。

　この図で丸印を「ノード」と呼び、ノードを接続している線を「辺」と呼ぶことにします。

　あやめデータには4つの変数があり、それらをx₁,……,x₄で表しています。これらに対応するノードを入力層と呼びます。次の層に当たる中間層はv₁,…,v₄の4つから構成されています。それぞれの辺には重みが対応付けられていて、x_iからv_jの重みをw⁽¹⁾_ijとします。例えば、v₁の値の計算は、x₁,……,x₄の重み付き和にバイアス項b⁽¹⁾₁を加えたものにアクティベーション関数（活性関数）h⁽¹⁾を作用させたものを考えます。つまりv₁の値は次のような式で与えられます。

　ここでの活性化関数h(1)には「ReLU（Rectified Linear Unit：正規化線形関数）」と呼ばれるものがよく使われます。ReLUは次で定義されます。

　次の中間層から出力層への計算も同様に重み付け線形和とアクティベーション関数の組み合わせで定義されます。

　ノードv_iからy_jへの重み付けをw⁽²⁾_ijとすると、y_jは次のように表されます。

　ここでのy_jは出力層で、分類問題の出力層に対するアクティベーション関数にはsoftmax関数がよく使われます。この場合のsoftmax関数は次で表されます。

　これはv_jを決めるのにv₁,v₂,v₃の値が必要になるので実際には「softmax(v_j;v₁,v₂,v₃)」と書くべきものなのかもしれません。しかし、これは線形和とアクティベーション関数で表されるという点では入力層から中間層への計算と共通です。

　最終的に分類を行うには、y₁,y₂,y₃のうち一番大きいものをラベルとして採用します。実際の分類データは0,1,2の値を取るので、y_jが一番大きいときにはj-1に分類すると思ってください。このように、n個の出力変数のうち値が最大のもののインデックスを分類値とする手法を「ワンホットエンコーディング」と呼びます。

　学習フェーズでは、訓練データを使って重み係数wやバイアス項bの値を調整し、できるだけ正しい出力を出すようにするのがニューラルネットワークです。パラメーターを調整するアルゴリズムの詳細については、ここでは触れないこととします。

　以上で、あやめデータを例にニューラルネットワークの仕組みを説明しました。あやめデータの例では入力層のノードと出力層のノードについて全ての組み合わせが辺でつながれています。一般には、データの性質などを考慮しながら「どのノードとどのノードをつなぐか」を考えます。ノードがつながれているのは変数の値を決定するのに依存関係があることを意味します。辺には重みが対応付けられるので辺が増えると計算量が増え、学習フェーズに時間がかかることになります。

　例えば、入力が画像データの場合には入力ノードの数はピクセル数（グレースケールの場合）またはピクセル数×3（RGBで表現されるカラーの場合）になるので、入力層と中間層の全ての組み合わせを辺でつなぐと辺の数が非常に大きくなってしまいます。

　また、中間ノードの数を幾つにするかも自由で、一般には実験をしながらちょうどいい数を決定します。あやめの例では中間層が1層しかありませんが、一般には複数の中関層があることもあります。

　このように、中間層の数が多い（2層以上）ニューラルネットワークによる学習を「ディープラーニング（深層学習）」と呼びます。

　以上のことをまとめると、学習を始める前にネットワークの構造を決定する必要があり、決定すべき事項には、中間層の数、ノードの数、どのノードを辺でつなぐか、などが含まれます。それらの決定は、過去のノウハウや実験の結果などにより行います。

あやめの分類の実装

　あやめの例を実装してみます。繰り返しますが、本稿ではKerasを使います。

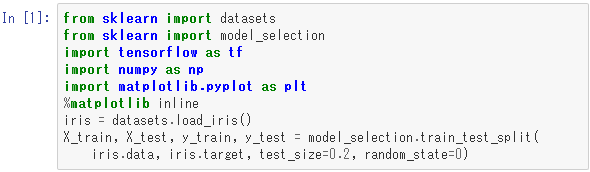
　まずはデータを準備します。

　ここでは、あやめデータをランダムに並べ替えて、最初の20％をテスト用として、残りを訓練用として分離しています。

　次にニューラルネットのモデルを作ります。

　外側の「tf.keras.models.Sequential」クラスは、層を順に並べることでネットワークを定義することを意味しています。

　最初の「tf.keras.layers.Dense(4, activation=tf.nn.relu)」が、入力層に接続する中間層に対応します。「Dense」クラスは、上位層との密な結合（つまり上位層との全ノードのペアについて辺がある）であることを示しています。Denseの第1引数は次層のノード数を示しています。activationとは、アクティベーション関数を示していて、ここではReLUを使っています。次に出力層の定義として、「tf.keras.layers.Dense(3, activation=tf.nn.softmax)」を与えています。これも中間層と密に接続しています。アクティベーション関数はsoftmaxを使っていますが、これは前述の通り分類問題の出力層によく用いられるもので、結果はワンホットエンコーディングになります。

　このコードとネットワーク図を関連付けると下図のようになります。

　ネットワークを定義した後は、損失関数や最適化アルゴリズムなどの指定をしてコンパイルします。

　ここで「optimizer="adam"」は最適化アルゴリズムの指定で、「adam」という手法を使うということです。アルゴリズムの詳細はここでは説明しませんが、adamは多くの場合に有効な手法です。

　「loss="sparse_categorical_crossentropy"」では損失関数を指定しています。この例は、出力がワンホットエンコーディングされているのに対し、訓練用データのラベルが0〜2の分類値で与えられているので、こういう場合には「sparse_categorical_crossentropy」という損失関数が利用できます。

　metrics=["accuracy"]というのは計算過程で何を表示するかを指定します。ここではaccuracy、つまりどのくらい正しく予測できているかを表示します。

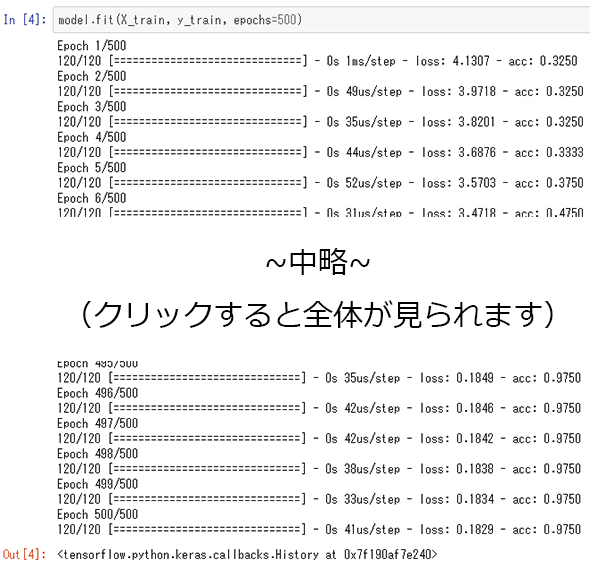
　次に、訓練データを使って学習させてみます。

　テストデータに対する予測値を計算してみます。

　テストデータに対してどのくらい正解できているかを見てみます。

　100％正しく分類できていることが分かりました。学習時に乱数を使っているので、この結果は異なることがあるので注意してください。