[Python入門]集合:Python入門(3/4 ページ)
集合の和/差/積/対称差を求める
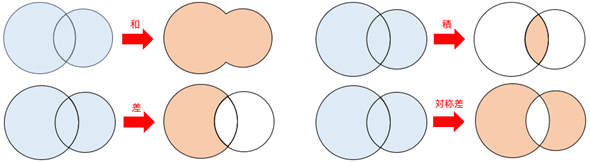
集合が複数あるときには、それらを基に次のような集合を求められる。
- 和:複数の集合に含まれる全ての要素で構成される集合を求める
- 差:ある集合に含まれるが、他の集合には含まれないものを要素とする集合を求める
- 積:複数の集合に共通する要素で構成される集合を求める
- 対称差それぞれの集合のみに存在する要素で構成される集合を求める
Pythonではこれらを求めるのに以下のメソッドと演算子が使える。
| 求める集合 | メソッド/演算子 |
|---|---|
| 和 | unionメソッド、|演算子 |
| 差 | differenceメソッド、-演算子 |
| 積 | intersectionメソッド、&演算子 |
| 対称差 | symmetric_differenceメソッド、^演算子 |
| 和/差/積/対称差を求めるメソッドと演算子 | |
なお、これらは2つ以上の集合を基に、新しく集合を作成し、それを戻り値あるいは演算の結果とするものだ。元の集合を更新するメソッドや演算子もあるが、それらについては後述する。
メソッドの構文は次の通りだ。
union/difference/intersection/symmetric_differenceメソッド
union(*others)
difference(*others)
intersection(*others)
symmetric_difference(*others)
元の集合と、*othersに渡された1つ以上の集合から、unionメソッドは和を、differenceメソッドは差を、intersectionメソッドは積を、symmetric_differenceメソッドは対称差を求める。
| パラメーター | 説明 |
|---|---|
| *others | 和/差/積/対称差の算出に使用する集合もしくは反復可能オブジェクト。複数の集合や反復可能オブジェクトをカンマ区切りで並べてもよい |
| union/difference/intersection/symmetric_differenceメソッドのパラメーター | |
メソッドには集合以外に反復可能オブジェクトも引数に指定できるのは、上で見たissubsetメソッド/issupersetメソッドと同様だ。演算子は集合のみを演算対象とするのも同様である。ただし、演算子では「集合1 | 集合2 | 集合3 | ……」のように3つ以上の集合を演算子でつなげられる。演算結果は新たな集合なので、「集合1 | 集合2 | 集合3」は「新しい集合1 | 集合3」となり、最終的には「新しい集合2」が得られるからだ(これに対して、>=演算子などがこれをできなかったのは、その演算結果がTrueかFalseとなるからだ)。
以下では、上記のメソッドや演算子を使って、和/差/積/対称差を求めてみよう。
和を求める:unionメソッド
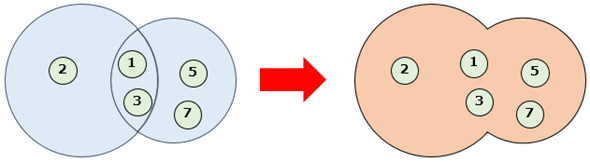
2つ(またはそれ以上)の集合があるとき、それらの全ての要素を含んだ集合のことを「和」(和集合)と呼ぶ。
Pythonで集合の和を求めるにはunionメソッドと|演算子が使えるのは既に述べた通りだ。以下に例を示す。
myset1 = {1, 2, 3}
myset2 = {4, 5, 6}
myset3 = {1, 3, 5, 7}
myset4 = myset1.union(myset3)
print(myset4)
myset4 = myset1 | myset2 | myset3
print(myset4)
以下に実行結果を示す。
差を求める:differenceメソッド
ある集合から、別の集合に含まれている要素と重複する要素を削除したものを「差」と呼ぶ。
Pythonで集合の差を求めるには、differenceメソッドもしくは-演算子を使用する。以下に例を示す。
myset1 = set(range(7)) # {0, 1, 2, ……, 6}
myset2 = {x for x in range(4, 9, 2)} # {4, 6, 8}
myset3 = {x for x in range(0, 4, 2)} # {0, 2}
myset4 = myset1.difference(myset2)
print(myset4)
myset4 = myset1 - myset2 - myset3
print(myset4)
以下に実行結果を示す。
元の集合となるmyset1には0〜6の整数値が含まれている。集合myset2には4、6、8が含まれていて、myset3には0、2が含まれている。よって、「集合myset1と集合myset2の差」は上の図に示したように「{0, 1, 2, 3, 5}」となり、「集合myset1と集合myset2、myset3の差」は集合myset1から偶数値を取り除いた「{1, 3, 5}」になる。
積を求める:intersectionメソッド
積とは、複数の集合に共通して含まれている要素からなる集合のことだ。
Pythonでこれを求めるには、intersectionメソッドもしくは&演算子が使える。以下に例を示す。
myset1 = set(range(1, 6)) # {1, 2, 3, 4, 5}
myset2 = set(range(2, 7, 2)) # {2, 4, 6}
myset3 = {x for x in range(6) if x % 2} # {1, 3, 5}
myset4 = myset1.intersection(myset2)
print(myset4)
myset4 = myset1 & myset3
print(myset4)
以下に実行結果を示す。
ここでは集合myset1には1〜5の範囲の整数値が含まれている。集合myset2は「2, 4, 6}」となっている。集合myset3は「{1, 3, 5}」だ。よって、集合myset1とmyset2の積は共通する要素を含んだ「{2, 4}」になる。また、集合myset1とmyset3の積も共通する要素を含んだ「{1, 3, 5}」(集合myset3と同じもの)になる。
対称差を求める:symmetric_differenceメソッド
集合Aと集合Bがあるとき、集合Aにあって集合Bにない要素と、集合Bにあって集合Aにない要素、これら2つの要素で構成される集合のことを対称差という。
Pythonで集合の対称差を求めるには、symmetric_differenceメソッドもしくは^演算子を使える。以下に例を示す。
myset1 = set(range(4)) # {0, 1, 2, 3}
myset2 = set(range(2, 6)) # {2, 3, 4, 5}
myset3 = set(range(-2, 2)) # {-2, -1, 0, 1}
myset4 = myset1.symmetric_difference(myset2)
print(myset4)
myset4 = myset1 ^ myset3
print(myset4)
実行結果を以下に示す。
この例では、集合myset1には0〜3の範囲の整数値が、集合myset2には2〜5の範囲の整数値が、集合myset3には-2〜1の範囲の整数値が含まれている。そして、symmetric_differenceメソッドで集合myset1とmyset2の対称差を求め、次に^演算子で集合myset1とmyset3の対称差を求めている。前者では集合myset1のみに存在する要素(0、1)と、集合myset2のみに存在する要素(4、5)だけを含んだ新たな集合が作成されている。次の演算の結果も同様だ。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 実行結果
実行結果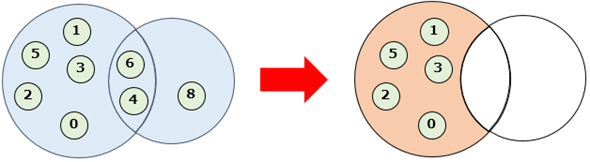
 実行結果
実行結果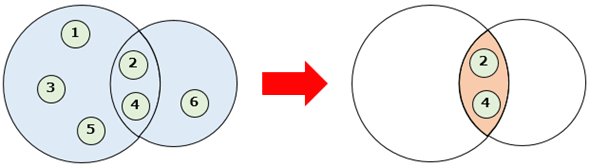
 実行結果
実行結果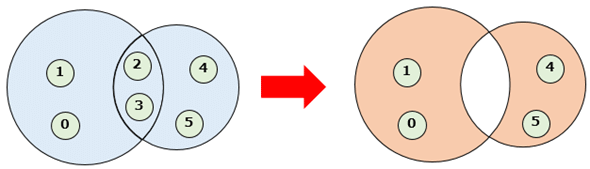
 実行結果
実行結果



