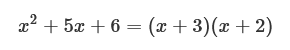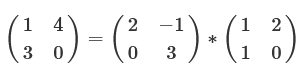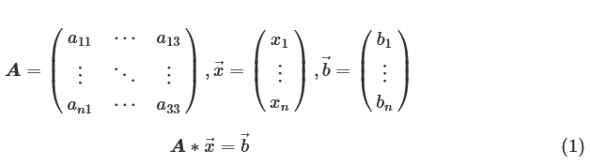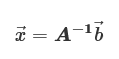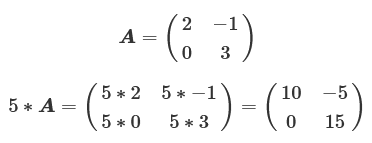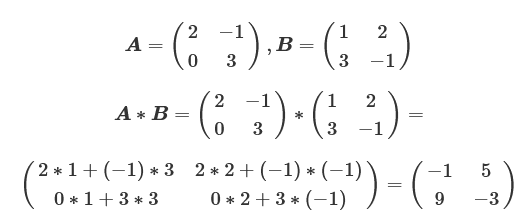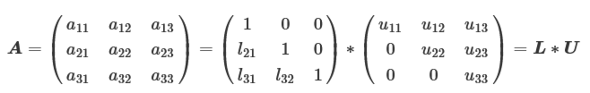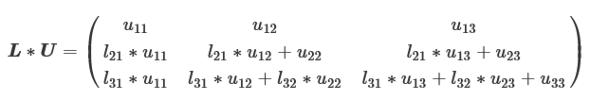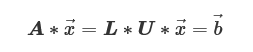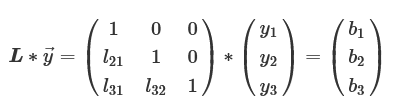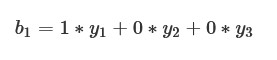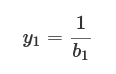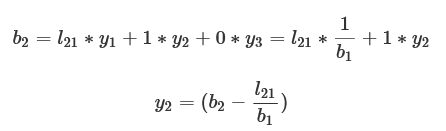機械学習やレコメンドでよく見る「特徴量」の本質とは――「行列分解」の基本を図版とPythonコードで理解する：「AI」エンジニアになるための「基礎数学」再入門（14）

AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は行列の計算分解について、図版とPythonコードを交えて解説します。

[原拓自，東京ITスクール]

　AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は「行列計算」について学びました。今回のテーマは、「行列の計算分解」です。

　前回、データを分析する際には、基本的に1次元のベクトルデータではなく多次元のデータを用いることが多いので、行列計算が重要になると解説しました。行列の計算は、AIが行う計算でもよく使用されており、さまざまな分析に関わる教科書などは行列表記での説明がほとんどです。今回紹介する「行列分解」は、そんな行列計算の中で重要なテクニックの一つです。

　行列分解をする理由や行列分解後に得られる結果の意味などについて、数式の内容よりも意味の解釈に注力して解説するので、そこに注目して学習してください。

行列分解をする理由

　初めに「行列分解とは何か」を説明します。行列分解とは、ある行列を行列の積に分解することを意味します。中学生の時に学習する「因数分解」の行列版です。昔を思い出すと因数分解は足し算や引き算で表されている数式をカッコ付きの掛け算の形にすることでした。下記のようなものです。

　行列分解は、これを行列で行うものです。行列に対する行列分解の例は次のようになります。

　このように、行列分解はある行列を別の行列の積に分解することです。また上記の行列分解は一例であり、一般に行列分解は次数が同じ「行列の積」ではない場合でも分解できます。行列の積については、前回詳しく説明しているので、知りたい方は参照してください。

　例で用いた行列分解は特に意味のあるものではありませんが、業務で使う行列分解は、「ある特定の形に分解すること」を目的とします。行列を分解する目的は大きく分けて2つあります。

　1つ目は計算上の実用的な理由で、計算量（計算時間）を減らすためです。そもそも実はPCで計算する場合でも行列計算をするには多くの計算量を必要とします。そこで、この計算量が少なくなり、より効率的に計算できる形に行列分解してから行列計算することがあります。

　2つ目はAIがデータを要約してデータが持つ系統的な性質を取り出すためです。ただ眺めるだけでは分からなかった行列データを分解することで見えてくることが多々あります。このような行列分解は画像処理や推薦システムなど幅広い分野で用いられています。

計算量を減らす行列分解

　前回の解説で「行列は連立1次方程式を解きやすくするために行列が作られた」と説明しました。連立1次方程式を行列とベクトルの積で表し、行列の逆行列を求めてその積を計算することで連立1次方程式を解くことができます。行列をA、ベクトル「→x」「→b」とすると、連立1次方程式は下記のよう表せます。

　Aと→bが既知の場合、（1）式の→xは、Aの逆行列「A^-1」を求めると下記のように式を変形して求めることができます。

　しかし、実は逆行列を直接Aから求めて連立1次方程式を解くやり方は推奨されていません。次数が大きい行列（行数、列数が大きい行列）の場合は必要とされる計算時間が膨大になるという実用面での問題が存在するからです。この計算量を減少させて連立1次方程式を解く数学のテクニックとして行列分解が用いられます。

行列演算の計算量

　次数が大きい行列では、どの程度の計算量になるのかを解説します。

　まずは、スカラーと行列の積を考えてみます。2行2列の行列の行列Aの場合で考えると、スカラー値「5」との積は次のようになります。

　2行2列の場合は行列の要素が4個存在するので、その計算回数は4回（つまり次数の2乗個）になります。よってN次の正方行列（N行N列の行列）ではN²回の乗算をする必要があります。単純な掛け算ですが、3次の正方行列では計算回数が9回、10次になると100回と次数が大きくなるにつれて計算量が飛躍的に上がっていきます。

　次に、行列同士の積での計算回数を確認します。2行2列のある行列A、Bの積を考えると次のようになります。

　この場合は、4要素（次数の2乗個）について計算されていますが、各要素を計算するためにAの行要素とBの列要素の内積が必要になるので、各要素で2回の乗算が行われています。この2回の乗算が要素数分の4個必要になるので、2×4の計8回の乗算をすることになります。さらに、行列の積では各要素内で和も計算しており、こちらは1回（次数-1）の和が要素数分必要なので、1×4の計4回存在します。これをN次の正方行列同士の積で考えると、乗算がN³回、加算がN²*（N−1）回必要になります。つまり、10次で1000回の乗算と900回の加算を計算することになり、行列同士の積はスカラーと行列の積よりもさらに計算量が増えています。

　Pythonのコードでもこの計算を確認してみましょう。前回では「Numpy」の「dot」関数で行列の積を計算していましたが、行列の積による計算量理解のために、行列の積をfor文で記述します。また、積を行う行列は簡単のため、単位行列にしてあります（当然、積の結果は単位行列になります）。

import numpy as np
 
# 行列の次数を定義
N = 10
# N行N列の単位行列生成
A = np.eye(N) 
B = np.eye(N)
# 行列の積の結果を格納する行列定義
C = np.zeros((N,N))
 
# 行列の積計算
for i in range(N):
    for j in range(N):
        for k in range(N):
            C[i,j] += A[i,k]*B[k,j]

　このコードを見ると、for文を3回使用しているのが分かります。各for文でN回実行されるのが、独立して3つあるので、N³回の計算が必要になっています。Nを大きくしていくと計算時間が飛躍的に長くなるので試してみてください。

　また、一般的な「掃き出し法」を用いて逆行列を求めた場合、必要となる計算の回数は行列の積と同様に乗算がN³回に、減算がN²*（N−1）回必要になります。つまり、行列の積同様N³回に比例する計算量が必要です。よって、逆行列を求めてその逆行列の積を求める場合でも次数が大きい場合に計算量が膨大になります。

LU分解

　ここまでで、行列の積や逆行列の計算には計算量が膨大になり、実用面で難があることが分かったと思います。ここからは行列分解することで計算量がどう変化するかを解説します。計算量削減の行列分解方法は多々ありますが、その中でも基本的な「LU分解」について説明します。

　LU分解とは、正方行列を「下三角行列」である「L」と「上三角行列」である「U」の積に分解するテクニックです。「三角行列」とは正方行列の対角線より上または下が全て「0」になっている行列のことです。また、Lの方は三角行列になっているだけではなく、対角成分が全て「1」になります。3次の正方行列でLU分解を式で表すと次のようになります。

　L、U自体の行列の求め方はL*Uを計算すると下記のようになるので、各要素とAの要素を比較することで求めることができます。

　この分解を式「A*→x」に適応すると、下記のように式を変形できます。

　また、U*→xを「→y」と置くことで、さらに上式は2つに分解できます。

　三角行列は行列の一部が0となっているので、この2つの式は簡単に計算できます。例としてL*→y式の計算を示します。

　y₁は行列とベクトルの積により、次のようになります。

　この式をy₁について書き直せば、次のようになります。

　y₂についてもb₂を計算し、先ほど求めたy₁を代入してy₂について書き直すと、次のように求めることができます。

　y₃についても同様に計算することで→yが簡単に求めることができます。

　このように各式の前から逐次的に処理していく方法が「前進代入」です。一方、U*→x＝→yは、計算方法こそ同じですが三角行列の形がLとは逆になるので、その処理は「後退代入」といいます。

　L*→yを計算して→yを求め、その→yを用いてU*→xを同様な手順で計算することで→xを導出することが可能になります。連立1次方程式を解く際に、LU分解を用いる方法と逆行列を求める方法での計算量をまとめると、下記のようになります。

• 【a】逆行列を求めて、逆行列とベクトル→bとの積を求める
  1. 逆行列（掃き出し法）を求める
     • 乗除算：N³回
     • 加減算：N(N-1)²回
  2. 求めた逆行列とベクトル→bの積を計算する
     • 乗除算：N²回
     • 加減算：N(N-1)回
• 【b】LU分解を行い、2つの三角行列とベクトル→y,→xの式を解く
  1. LとUの三角行列に行列分解する
     • 乗除算：(N-1)(N²+N+3)/3回
     • 加減算：N(N-1)(2N-1)/6回
  2. LU分解で得た2つの式を前進代入と後退代入で計算する
     • 乗除算：N²回
     • 加減算：N(N-1)回

　【a】【b】共に、リストの2.の処理で必要な計算量が同じなので、差が生じるのはリストの1.の逆行列を求めることと、LU分解による計算量です。この差はN³にかかる係数がLU分解の方の場合は3分の1なので、計算量（計算時間）は約3分の1になります。

　Pythonのコードでもこの差を確認してみましょう。

import scipy.linalg as linalg
import time
 
N = 10000
A = np.random.rand(N, N) # 乱数でN行N列の行列作成
b = np.random.rand(N) # 乱数でN次ベクトル作成
 
start = time.time() # 計算スタート時の時間
inv_mat = np.linalg.inv(A) # 逆行列計算
x_1 = np.dot(inv_mat, b) # 逆行列とベクトルの積計算
elapsed_time = time.time() - start # 計算時間の計算
print ("elapsed_time:{0}".format(elapsed_time) + "[sec]")
 
start = time.time()
LU = linalg.lu_factor(A) # LU分解計算
x_2 = linalg.lu_solve(LU, b) # 前進代入、後退代入で計算
elapsed_time = time.time() - start
print ("elapsed_time:{0}".format(elapsed_time) + "[sec]")

　PCのスペックなどにも寄りますが、筆者の環境では下記のような結果になりました。LU分解を用いた計算の方が確かに3分の1ほど短くなっています。

elapsed_time:20.145538806915283[sec]
elapsed_time:6.22236180305481[sec]

データを要約する行列分解

　データ分析においても行列分解を行う手法があります。その目的は主にデータを“要約”することにあります。ここではAIによる推薦システムを用いてこの内容を説明します。

　ECサイトなどで商品を買ったユーザーに対して、別の商品をレコメンドする推薦システムはECサイトのみならず、インターネット上のさまざまなサービス（「Netflix」など）で実装されているので、レコメンドを経験されたことがある方は大勢いると思います。この推薦方法は単純に売れ筋の商品を薦める場合もあれば、個人ごとの傾向を考慮して薦める場合もあります。つまり、特定のユーザーが気に入りそうなアイテムを過去のデータに基づいてレコメンドする仕組みです。

　このレコメンドの手法にはさまざまなやり方がありますが、ここでは行列分解を用いたレコメンドのやり方を解説します。

レコメンドに用いる行列分解

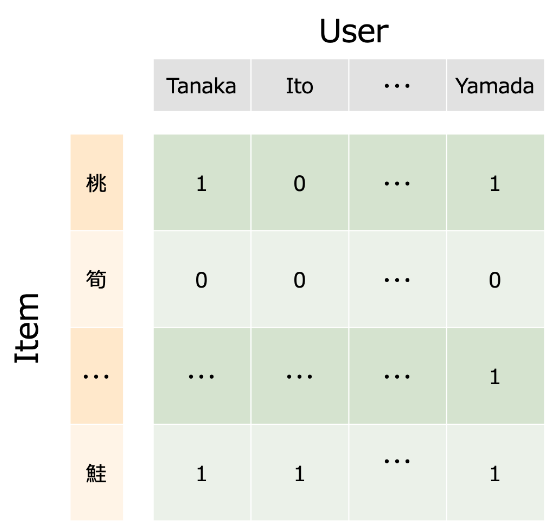
　まず、レコメンドするためのデータがどういったものかを紹介します。ここで考えるのはあるECサイトの登録者に対して誰が何を買ったかを記録した購買データです。下図を見てください

　行列の横列がユーザーを表し、縦列が商品を表しており、各ユーザーが買った商品の購買履歴が縦列で示されています。このデータでは購買した商品には1、未購買の商品に関しては0で埋めています。

　購買データをミクロ視点で見ると、個々のユーザーはそれぞれ固有の意図を持って商品を購入しています。しかし、「ユーザーの集団」といったマクロ視点で見ると、ある傾向を持っていることがあります。例えば、日用品を購入するユーザー群や食物を購入するユーザー群などです。

　個々の商品やユーザーだけ見てもこのパターンはなかなか発見できませんが、全体のデータを要約して存在する系統的なパターンを取り出せたら、この購買データをより理解できそうです。商品を人間がカテゴリー分解（日用品、食品など）してそのカテゴリーで集計すれば、ある程度のパターンは分かりますが、カテゴリーにない商品の組み合わせなどが存在していた場合には対応できません。

　また、購買データのような膨大なデータの場合、全データの組み合わせを人間が考えてそれぞれの傾向を求めることは計算上の問題で現実的ではありません。さらに、商品数が多いために未観測で正確なデータがあり、「その商品に興味がないのか、その商品を知らないのか」が不明なので、この購買データをそのまま分析することは難しいでしょう。

　このようなデータに対しての要約作業を行ってくれるのが行列分解です。

　先ほど説明した購買データに潜む本質的なユーザーの趣味、嗜好（しこう）を行列分解でどう抽出するかを説明します。その方法とは元の購買データをユーザーに関する情報が詰まった行列と商品に関する情報が詰まった行列に分解することです。

　ここでいう「情報」は購買データが持つ潜在的な“特徴”です。ユーザーの特徴を持つ行列と商品の特徴を持つ行列があり、それぞれの積で元の購買データになるという考えです。つまり、購買データの1や0はユーザーと商品の行列で、それぞれの特徴が「そろっていれば、1」「そろっていなければ、0」といった“解釈”です。

　この特徴は与えられた購買データから数学的に計算されるので、人間が理解できる特徴となっている保証はない点に注意しなければいけません。

「Matrix Factorization」を用いた行列分解

　先ほど説明した購買データでの行列分解を詳説します。この行列分解の目的は購買データの個々のユーザーと商品のデータを見るのではなく、それぞれの“性質”を抽出することでした。この手法は行列分解においてもさまざまなものがありますが、ここではその一つ「Matrix Factorization」について解説します。

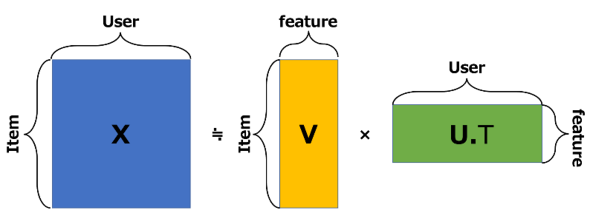
　Matrix Factorizationでは購買データの行列「X」があるとき、この行列を下記のような2つの行列「V」「U」に近似的に分解します。

　Vは特徴量×商品数の行列であり、Uは特徴量×ユーザー数の行列です。上式では行列の積では積を行う行列の行数と列数がそろっていなければならないので、Uは特徴量が列となるように行列を反転させる“転置”（「^T」を付けて表現します）を行った「U^T」という表記になっています。図で示すと下記のようになります。

　「Item」の行列Vは商品に関する情報が詰まった行列であり、それぞれの商品が縦に、横にはその商品の特徴が並んでいます。ここでいう「特徴」は、先ほど述べた「潜在的な特徴」です。この行列が商品だけで要約されたデータです。同様に、「User」の行列Uはユーザーが横に、縦にはそのユーザーの特徴が並んでいます。今ある特徴量で商品とユーザーを分解しましたが、これは「このように分解できたら情報が要約できる」という考えの下で行った分解であり、この行列の積が購買データと全く同じになる行列分解が存在する保証はありません。

　これらの行列の積が元の購買データ（正確には観測されたデータ）をなるべく再現するように、V、Uを求めます。各行列の特徴量を増やせば、表現力が上がるので、元の購買データを復元できる行列になりますが、そうした場合にはせっかく特徴量を用いて要約した意味がなくなってしまいます。

　最後に、この行列分解をした結果、何がうれしいのかを説明します。

　行列分解を行ったことでユーザーや商品ごとの特徴を求めることができました。性質がバラバラだったユーザーや商品が特徴量でグループ化されたことになります。ユーザーの場合で考えると、特徴量の数がユーザー数よりもずっと少ない場合、そのユーザーたちの性質が特徴量のパターンでまとめられたことになります。例えば、ユーザー数が10万で特徴量の数が5だった場合、全ユーザーはこの5つの変数で表現されます。10万人の個々の性質をたった5つで表現することが可能になり、ユーザーをまとめることができます。

　さらに、分解した商品とユーザーの行列から再現した購買データには元の購買データでは未観測だった購買データを推測できるようになっています。個々のユーザーでは未観測だったデータが、要約することで類似した集団と同様な傾向を持つと見なされ、同じような購買パターンとして再現できるのです。つまり、一度行列分解して再度構築した購買データを用いると、あるユーザーの商品購買可能性を知ることができます。この情報を用いることで、そのユーザーに最適なレコメンドをすることができます。

まとめ

　下記は今回のまとめです。

• 行列分解には大きく分けて、計算の実用的なものとAIが行う分析の2つが存在する
• 連立方程式を解くには逆行列を用いるよりも、行列分解して解く方が計算量を抑えられる
• 購買データを行列分解し要約した後で再構築することで、未観測だったデータを推測できる

筆者紹介

原 拓自（はら たくじ）

1988年、岐阜県生まれ。大学院では宇宙物理を専攻し、卒業後はデータサイエンティストとしてキャリアをスタートする。

さまざまな会社で分析コンサルを経験した後、世界最大の外資系ECサイト会社でデータサイエンスの知識を深める。

現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。