統計学や機械学習でもよく使われる相関係数が分かるベクトル計算の基礎知識:「AI」エンジニアになるための「基礎数学」再入門(12)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は「ベクトル」の計算と、その応用、相関係数について、図版とPythonコードを交えて解説します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は「スカラ」「ベクトル」「行列」「テンソル」の基礎知識を学びました。今回のテーマは、ベクトルの扱い方=計算方法です。
ところで、皆さんは英語を学習したことがあると思います。新たな英単語・英文法を学ぶことで、より多くの英文を読解できるようになることを経験しているはずです。何が言いたいかというと、今回のテーマを学ぶことは、数学に関連する文献を読むことにおける「単語や文法を学ぶ」ようなことに値します。つまり、より多くの文献を読解できるようになるはずなので、しっかり学んでいきましょう。
2次元のベクトル
ベクトルの計算方法を解説するために、例として次のような2つのベクトルを考えます。
今回は2次元(要素が2つ)のベクトルで、次のような数字の集まりとします。
Pythonのリストで表現すると、次のような具合です。
vec_a = [1, 3**0.5] vec_b = [2*3**0.5, 2] vec_a, vec_b # ([1, 1.7320508075688772], [3.4641016151377544, 2])
今後の説明は上記のベクトルを使用します。
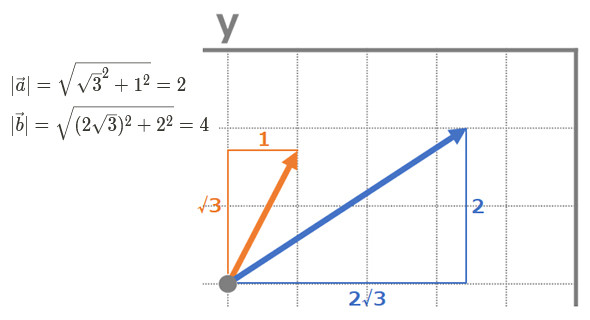
長さの計算
ポイント
- 長さは三平方の定理で算出
- 掛け算でも使用する必須内容
ベクトルには長さという概念があります。
長さを表す記号は|<ベクトル>|です。先ほどのベクトルaの長さの場合、下記のように書きます。
計算方法は三平方の定理を用いて考えると分かりやすいでしょう。
三平方の定理(ただし直角三角形のみにおいて)
斜辺2=底辺2+高さ2
従って、各ベクトルの長さは次の通りです。
Pythonコードで結果を確認してみます。
# numpyならば np.linalg.norm で計算できる
def get_length(vec):
sq = [e**2 for e in vec]
return sum(sq)**0.5
get_length(vec_a), get_length(vec_b)
# (2.0, 4.0)
なお、長さの概念は、この後の掛け算部分に関連するので押さえておきましょう。
足し算
ポイント
- ベクトルの合成
- 計算は対応する位置の要素(スカラ)を足し合わせるだけ
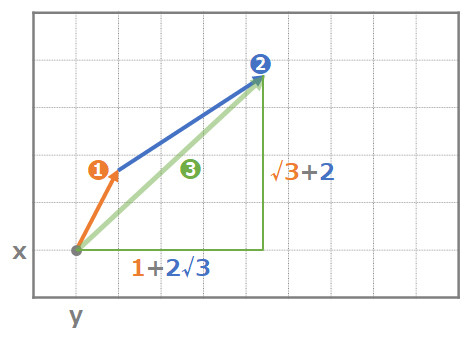
足し算について、まずはイメージを捉えていきましょう。足し算はベクトルの合成を表します。
どのように合成をするかというと、次のような手順です。
- 一方のベクトルを描く
- もう一方のベクトルを、1.のベクトルの先を起点に描く
- 原点から2.のベクトルの指すベクトルを描く
3.で描かれたベクトルが「合成されたベクトル」です。
イメージがつかめたら計算方法を確認してみましょう。計算方法は簡単で、対応する要素同士で足し算をするだけです。Pythonで確認してみましょう。
def add_vec(vec1, vec2):
return [e1+e2 for e1,e2 in zip(vec1, vec2)]
add_vec(vec_a, vec_b)
# [4.464101615137754, 3.732050807568877]
引き算
ポイント
- ベクトルの先と先をつなぐ
- 引き算も足し算と同様に計算できる
さて、一方で引き算のイメージは簡単です。
引き算のベクトルは次のような手順で描けます。
- 引く側のベクトルの先から、引かれる側のベクトルの先まで矢印を伸ばす
- 1.の矢印を、矢印の矢尻が原点に合うようにスライドさせる
2.(図の【2】)の矢印が引き算後のベクトルです。
計算方法は足し算と同様です。次のように考えましょう。
足し算と同様に計算できます。こちらも、Pythonで確認してみましょう。
vec_a = [1, 3**0.5]
vec_b = [2*3**0.5, 2]
def subt_vec(vec1, vec2):
return [e1-e2 for e1,e2 in zip(vec1, vec2)]
subt_vec(vec_a, vec_b)
# [-2.4641016151377544, -0.2679491924311228]
掛け算
ベクトルの掛け算には、内積、外積の2種類があります。それぞれ計算結果の表す意味が異なるので確認していきましょう。
なお、掛け算と割り算は表裏一体のように思えるものの、実はベクトルに関しての割り算は定義されていません。よって、今回は掛け算のみ解説します。
内積
ポイント
- ベクトル間の角度を算出するための計算法
- 計算は対応する要素の掛け算をして合計するだけ
内積は2つのベクトルの間の角度を求めるための計算です。2つのベクトル間の角度は類似度(角度が小さいほど同じ方向を指しているので似ている)とも解釈できるので、統計学や機械学習でもよく使われます。
なお、内積は別名「ドット積」と呼ばれ、下記のように記述されます。
計算方法は次の通りです。
さて、この計算結果は何を表すでしょうか。それを知るには、次の内積の性質を知る必要があります。
ここで右辺に角度に関するものが出てきました。cosθのθは2つのベクトル間の角度を表します。すなわち、次のことがいえます。
- cosθが1に近いほど2つのベクトルは同じ方向を向いている
- cosθが-1に近いほど2つのベクトルは別の方向を向いている
それでは、cosθの値を計算してみましょう。
vec_a = [1, 3**0.5]
vec_b = [2*3**0.5, 2]
def get_length(vec):
sq = [e**2 for e in vec]
return sum(sq)**0.5
def get_cos(vec1, vec2):
prod = sum([e1*e2 for e1,e2 in zip(vec1, vec2)]) # 内積
return prod/(get_length(vec1)*get_length(vec2))
get_cos(vec_a, vec_b)==3**0.5/2
# True
つまりは、次のようになります。
図で表すと次のようになることが分かります。
以上の通り、内積を計算することで2つのベクトルの角度を調べることができました。なお、内積の統計学的な応用を後述するので、ぜひ最後まで読み進めてください。
外積
ポイント
- 2つのベクトルに対して直角なベクトルを算出するための計算法
- 電磁気学など物理学領域で頻繁に使われる
- データ分析の枠組み内ではあまり使われない
外積は2つのベクトルに直角なベクトル(右手系)を算出するための計算です。データサイエンス回りでは、あまりお目にかかることはないので説明は割愛します。
ただし、電磁気学など物理学領域ではよく使われる計算方法なので知っておいて損はありません。
ベクトル計算の応用:相関係数
ポイント
- 相関係数は2ベクトル(=データ)の間の角度を表している
- 角度は類似度と捉えることができる
統計学を学んでいると「相関係数」という統計量に必ず触れることになります。
相関係数は必ず-1〜1の範囲に収まるもので、2つのデータにおける相関の強さを表します。なお、相関の強さは、別の言い方をすれば「データの類似度」ともいえます。
ここで疑問になるのは、相関係数はなぜ-1〜1なのか? そもそも何を表す数値なのか? という点かと思います。答えから言うと、相関係数は内積の部分で学んだcosθです。
これについてはPythonのコードを使って確認していきましょう。まずは、次のように5人の身体測定結果のデータがあると仮定します。
| 名前 | 身長 | 体重 |
|---|---|---|
| Aさん | 173 | 71 |
| Bさん | 165 | 66 |
| Cさん | 181 | 74 |
| Dさん | 177 | 74 |
| Eさん | 169 | 68 |
この身長と体重の相関係数を求めます。まずは、「numpy」で相関係数を求めてみます。
import numpy as np height = [173, 165, 181, 177, 169] # 身長データ weight = [71, 66, 74, 74, 68] # 体重データ np.corrcoef(height, weight)[0][1] # 相関係数算出 # 0.9722718241315028
次に、身長と体重のベクトルをそれぞれ標準化(連載第5回参照)して、標準化後のベクトル同士のcosθを求めてみます。
height = [173, 165, 181, 177, 169] # 身長データ
weight = [71, 66, 74, 74, 68] # 体重データ
def zscore(vec):
'標準化処理の関数'
mean = sum(vec)/len(vec) # 平均値
var = sum([(v-mean)**2 for v in vec])/len(vec) # 分散
std = var**0.5 # 標準偏差
return [(v-mean)/std for v in vec]
def get_length(vec):
sq = [e**2 for e in vec]
return sum(sq)**0.5
def get_cos(vec1, vec2):
prod = sum([e1*e2 for e1,e2 in zip(vec1, vec2)]) # 内積
return prod/(get_length(vec1)*get_length(vec2))
def get_corr(vec1, vec2):
# 標準化
z1 = zscore(vec1)
z2 = zscore(vec2)
return get_cos(z1, z2)
get_corr(height, weight)
# 0.9722718241315029
このように相関係数と標準化後ベクトルのcosθが一致しました(*丸め誤差により不一致だが、理論上一致する)。従って、相関係数は標準化後ベクトル同士の間の角度を表していることが分かります。
さて統計学には、訳の分からない複雑な統計量がたくさん登場するので理解に苦しむ場面が多くあります。しかし、今回のように他の分野の考えを持ち込むことで、新しい観点を得られたり、それによってすんなり解釈ができたりすることがあります。
よって、1つの内容の理解に苦しんだときは、1つの文献に固執することなく、別々の色んな解説を見てみることをお勧めします。
次回は、行列計算の解説
前回、行列はベクトルを並べたものだと解説しました。つまり、ベクトル計算を理解できれば行列計算を理解することができます。今回の内容はしっかり押さえて、次回の行列計算に臨みましょう。
関連記事
 Lesson 1 機械学習を始めるための、Pythonデータ構造「多次元リスト」入門
Lesson 1 機械学習を始めるための、Pythonデータ構造「多次元リスト」入門
Pythonの基本的な言語仕様では、データはどう表現できるのか? 単一の数値データから始め、1次元、2次元、……多次元と複数の数値データを表現できるリスト型のデータ構造まで、ステップ・バイ・ステップで見ていく。 第3回 TensorFlowの基本構成要素:「テンソル」と「セッション」
第3回 TensorFlowの基本構成要素:「テンソル」と「セッション」
TensorFlowによる深層学習を始める前に、TensorFlowの基本的な構成要素であるテンソルとセッションを理解しておこう。TensorFlowのコード例を示しながら、できるだけコンパクトにまとめる。 機械学習の基礎の基礎、行列計算に欠かせないNumPyの基本的な使い方
機械学習の基礎の基礎、行列計算に欠かせないNumPyの基本的な使い方
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。今回は、科学的計算の基本的パッケージNumPyを使って、配列の基本操作、スライシングとインデクシング、配列を使った簡単な計算の仕方などを紹介。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

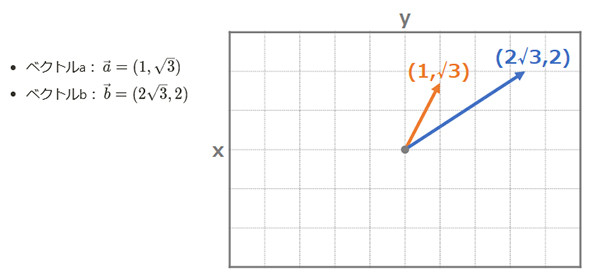 ベクトルa(オレンジ色)、ベクトルb(青色)の図
ベクトルa(オレンジ色)、ベクトルb(青色)の図