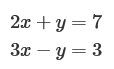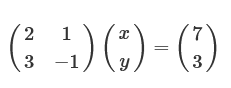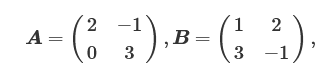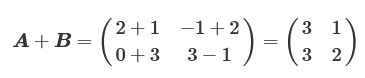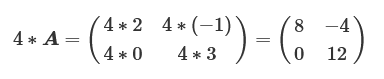画像変換などの機械学習でよく出るデータとパラメーターの関係が分かる「行列演算」の基礎知識：「AI」エンジニアになるための「基礎数学」再入門（13）

AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は行列演算や逆行列について、図版とPythonコードを交えて解説します。

[原拓自，東京ITスクール]

　AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は「ベクトル計算」について学びました。今回のテーマは、行列の計算方法（行列演算）です。行列演算が何を意味するのか、その本質について解説していきます。

　前回から計算についての説明が続いているので、普段数学に慣れていない方は難しく感じていると思います。特に行列演算は大学で学ぶ領域であり、数式の記述が多くなります。ここでは数学的な計算内容に注目するのではなく、行列演算が何に用いられているのか、その計算が表す意味について解説するので、その点に注目して学んでください。

なぜ行列は必要なのか

　行列演算について説明する前にベクトルと行列について、いま一度復習しましょう。前々回でベクトルとは「ひとまとまりの数字を縦か横に並べたもの」であり、行列はその「ベクトルを縦横の2次元に並べたもの」と説明しました。

行列は方程式を簡単に記述する

　では、この行列というものがなぜ数学で導入されたのでしょうか？　その背景には「方程式を簡単に記述する」という目的があります。例として下記の2つの方程式を考えます。

　数学では、このような複数の方程式（連立方程式）を用いて変数の値(x,y)を解くことがよくあります。このとき、上記の連立方程式は下記のように行列とベクトルを用いて表せます（詳細は後述）。行列の目的は、このような連立方程式の簡略化にあります。

　この連立方程式の解き方は高校数学で学習しますが、行列を用いることで簡略化できるだけではなく、別のやり方で(x,y)の値を計算することも可能です。本稿のゴールは、行列計算の方法と意味を理解して、上記のような連立方程式を行列計算によって求められるようになることです。

　なお対象となる連立方程式は、xやyなどの変数が常に「一次」である「一次方程式」に限定されます。このように、変数が一次である方程式を「連立一次方程式」といいます。

機械学習でよく出るデータとパラメーターの関係

　以前、「AIはデータに対して用意された数式を当てはめて、その数式が持つパラメーターを解いている」と説明しました。それと同じように例えると、数値で表現されている右辺、左辺の行列やベクトルがデータ、(x,y)という変数で表されたベクトルが数式のパラメーターを指します。

　行列とベクトルで表された式を見ると、行列とベクトル(x,y)の積が計算されて別のベクトル(7,3)になっていることが分かります。つまり、行列の積はある“入力”データ（今の例だとベクトル）を別の“出力”データに変換する性質を持っています。

　具体的な例でいうと、画像データ（行列）の拡大、回転など入力データを変換する操作がありますが、このようなデータの変換は行列の積で表現できます。

行列の演算方法

　ここからは基本的な計算方法を解説します。行列計算では一部スカラー同士の計算とは異なるルールがあるので、それも含めて説明します。

行列の和（差）とスカラー倍

　例としての下記2つの行列があるとします。

　これらの和は下記のようになります。

　行列同士の和（差も同様）は単純に行列の各要素の和です。互いに対応する要素同士の和なので、行列の和は互いの行列の形（縦横の数）が同じもの同士でないと計算できません。

　行列のスカラー倍したものは、単純に各要素をスカラー倍したものになります。

　上記の計算をPythonで記述すると下記のようになります。

import  numpy as np
 
# 行列の定義
A = np.matrix([[2 , -1], [0 , 3]])
B = np.matrix([[1 , 2], [3 , -1]])
 
# 行列の和
print(A + B)
 
[[3 1]
 [3 2]]
 
# スカラー倍
print(4*A)
 
[[ 8 -4]
 [ 0 12]]

行列とベクトルの積

　行列の積について説明します。行列の積はその計算方法が特殊なので、慣れるまで大変ですが、この行列の積が行列演算で最も使われるので、ぜひ覚えてください。まず先ほどの例で用いた行列Aと列ベクトル「→x」の積を考えてみます。それらの積は下記のようになります。

　計算過程において、行列の行要素と列ベクトルとの内積が計算されています。行列の行数は2つあるので、最終的に2つの要素を持つ列のベクトルが計算結果として導出されています。前述したように、行列の積は「変換」を意味し、この計算も列ベクトル→xが行列の積によって別の列ベクトルに変換されています。この計算は「行列Aが行ベクトルを2つ並べたもの」と考えると、理解しやすいと思います。

　つまり、行列の行を構成しているベクトルそれぞれに列ベクトルの内積を計算するという考えです。行列Aの行成分を「→A1,→A2」とする行ベクトルで表現して上記考えを式で記述すると下記のようになります。

　またこの計算をPythonで記述すると下記のようになります。NumPyの「dot」関数を使うと簡単に計算できます。

# 行列の定義
A = np.matrix([[2 , -1], [0 , 3]])
x = np.array([2,1])
# 行列の積
print(np.dot(A,x))
[[3 3]]

　行列とベクトルの積の理解を深めるため、前述したように行列の積が→xを別のベクトルに変換した様子を表したのが下図です。ベクトル(2,1)に行列Aが掛けられることで別のベクトル(3,3)に変換されています。

行列の掛け算の注意点

　ここまでで行列の掛け算の基本は理解できたと思いますが、注意しなければならないことが2点あります。

　1点目は掛け算する際、行列の行要素数と列ベクトルの要素数が同じでないと計算ができないということです。ベクトルの内積が同じ要素数を持つもの同士でしか計算できなかったのと同様に、行列の掛け算は行要素と列要素との内積を計算（先ほどの例だと行列の行と列ベクトル）するので、行列の積では内積計算の際に行要素数と列要素数が同じでないといけません。例えば、2行2列の行列と要素数3の列ベクトルは掛け算の計算ができません。

　2点目は掛ける順番によって結果が変わるということです。行列の掛け算は常に行要素と列要素での内積が計算されるので、掛ける順番が変わるとこの内積計算の中身が変わるので、結果が変わります。これを理解するために、先ほどの列ベクトルを行ベクトルにしてその積を考えてみましょう。行ベクトル→x^Tと行列Aの積は下記のようになります。

　この場合は行ベクトルに対して行列の列ごとに内積が計算されています。行ベクトルの行要素数が1、行列の列要素数が2なので、計算結果は1行2列の行ベクトルになっており、先ほどの計算と順番が変わったため結果も変化しています。こちらも先ほど同様に行列をベクトルで構成されたものと見立てて計算してみましょう。行列の列成分を「→A3,→A4」とする列ベクトルで表現して記述すると下記のようになります。

　このように「掛ける順番で計算結果が変わる」というのは、スカラーのときにはなかったことであり、行列の積の重要な性質です。

　Pythonによる計算は下記のようになります。

# 行列の積
print(np.dot(x,A))
 
[[4 1]]

行列同士の積

　最後に行列同士の掛け算についてです。これまで内容を応用するだけなので、難しく考える必要はありません。なぜなら、行列は行ベクトルや列ベクトルのまとまりとして考えることができるので、先ほどの計算とやることは変わらないからです。

　行列A、Bの掛け算は行列Aの行成分に対して行列Bの列成分との内積計算となり、下記のように計算されます。

　こちらも行列Aを2つの行ベクトルのまとまりとし、行列Bを2つの列ベクトルのまとまりとして考えると、下記のように記述でき、シンプルに計算過程を理解できます。

　行列とベクトルの掛け算と同じように、行列が掛けられたことによって今度は別の行列に変換されています。

　Pythonでの行列同士の計算は下記のようになります。

# 行列の積
print(np.dot(A,B))
 
[[-1  5]
 [ 9 -3]]

逆行列

　これまで行列の和（差）と積について解説してきました。では行列の割り算はどうなるのかと考えている方もいらっしゃるかもしれませんが、行列には割り算がありません。しかし、割り算と似た振る舞いをする「逆行列」というものがあります。

逆数とは

　逆行列の前にまず「逆数」について説明します。逆数とは、ある数に掛け算した結果が1となる数です。あるスカラーaの逆数は“a分の1”となります。なぜならaとa分の1の掛け算の答えは1となるからです。

単位行列とは

　この考えを行列にも応用したものが逆行列です。しかし、そのためにはスカラーの逆数のときに出てくる1と同様なものを行列でも定義しなければなりません。スカラーでの1に対応する行列は「単位行列」といい、単位行列は行列の対角成分のみ存在し、その値が全て1となる行列です。2行2列での単位行列は下記のようになります。

　単位行列はスカラーの1と同じような性質を持っています。どんな数字に1を掛けても結果が変わらないのと同じで単位行列を任意の行列に掛け算しても結果が変わることはありません。

　これは順番を変えても成り立ちます。

逆行列の計算方法

　この単位行列を用いると逆行列が定義できます。つまり掛ける順番にかかわらずある行列Xと掛け算してその結果が単位行列になる行列が逆行列（「X^-1」と記述します）です。行列Xと逆行列X^-1の積は下記のようになります。

　2行2列の行列Xに対する逆行列X^-1の求め方は下記のようになります。

1. 行列Xの対角要素を入れ替える
2. 非対角要素の符号を反転させる
3. 行列全体にある係数で割る

　この3ステップで逆行列が計算できます。最後のステップにあるこの係数は「行列式」といい、2行2列の場合「行列の要素の左上×右下−右上×左下」と定義されます。行列式は「|X|」「det(X)」と表せます。

　先ほどの3ステップで任意の行列Xに対する逆行列を求めてみます。

1．行列Xの対角要素を入れ替える

2．非対角要素の符号を反転させる

3．行列全体を行列式で割る

　逆行列を求めることができました。2行2列の場合、このように簡単に求めることができますが、行列の要素数が大きくなる（3次、4次……）につれて逆行列の計算方法は複雑になります。多くの場合、“逆行列を求めるためのアルゴリズム”を使って逆行列を求めます。

　次にこの2つの行列（XとX^-1）の掛け算が定義通り単位行列になることを確かめてみます。

　少し長くなりましたが、確かに逆行列を掛け算すると単位行列になることが確かめられました。

逆行列が計算できない場合

　逆行列で重要なのが行列式の値です。逆行列を求める過程で行列式の値で割るという計算をしていますが、もし行列式の値が「0」になることがあれば逆行列は計算できません。つまり逆行列が計算できない場合があります。

　行列の掛け算は“変換”するものだと前述しましたが、逆行列は、その変換を元に戻す行列です。つまり、元に戻せないように変換されたら、その逆行列は計算できません。「元に戻せない変換」とはどういったものか、スカラーの計算を例に簡単に説明します。

　2に3を掛け算した場合では結果を3で割れば当然元の2に戻ります。

　しかし、2に0を掛け算した場合ではどうでしょうか？

　この場合、どんな数を掛け算しても元の2に戻すことができません。これと同じようなことが行列の積でも存在し、行列式が0となる行列による変換は元に戻すことができません。

逆行列を用いた連立方程式の求め方

　逆行列を用いて本学習のゴール、連立方程式を解いてみましょう。本稿の最初に紹介した連立方程式は下記のように行列で表すことができました。

　行列をAとすると、下記のようになります。

　行列Aの逆行列を両辺に掛けることで上記式は下記のように記述できます。つまり、行列によって変換された結果に逆変換することで(x,y)を求めるということです。

　逆行列を求めて計算してみましょう。先ほどの定義から逆行列A^-1は下記のようになります。

　これを代入すると(x,y)が求まります。

　行列の演算を用いて逆行列を解くことができました。

　Pythonで計算するには下記を実行してください。

# 行列の定義
A = np.matrix([[2 , 1], [3 , -1]])
y = np.array([7,3])
 
# Aの逆行列の計算
inv_A = np.linalg.inv(A)
 
# 逆行列とyの積
print(np.dot(inv_A,y))
 
[[2. 3.]]

まとめ

　下記は今回のまとめです。

• 行列を用いると連立一次方程式を解くときに便利になる
• 行列の積はスカラーの積と計算ルールが異なり、特に掛ける順番によって結果が異なる
• 逆行列を用いて行列による変換を元に戻すことで連立一次方程式が解ける

筆者紹介

原 拓自（はら たくじ）

1988年、岐阜県生まれ。大学院では宇宙物理を専攻し、卒業後はデータサイエンティストとしてキャリアをスタートする。

さまざまな会社で分析コンサルを経験した後、世界最大の外資系ECサイト会社でデータサイエンスの知識を深める。

現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。