データ分析やAI予測の基本中の基本「回帰分析」「最小二乗法」の基礎をPythonコードと図で理解する:「AI」エンジニアになるための「基礎数学」再入門(15)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は「回帰分析」「最小二乗法」について、図版とPythonコードを交えて解説します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回まではSeason1として基礎を学んできました。
今回からはSeason2、応用編として下記の範囲を学んでいきます。
応用編初回のテーマは「最小二乗法」です。
データ分析やAI予測の基礎「回帰分析」とは、「最小二乗法」とは
皆さんは「Microsoft Excel」などで「回帰分析」を行ったことはあるでしょうか。
経験のある方は必見です。今回の記事を読めばモデル(=予測線)がどのように生成されるかが理解できます。これまでなんとなくポチっとボタンを押すと引かれていた線が、どのような線なのかが気になってきませんか。
なお、「回帰分析とは何ぞや?」という方のために説明すると、概要はこちらの通りです。
- 量的データ(連載第2回参照)の予測を直線で行う手法
- 図1は「アイスの販売個数」を「気温」を用いて予測する様子
図1のような線があれば「明日は27度になるそうだ」と分かり、「明日は240個ほどアイスが売れそうだ」と予測できるわけです。
2点を通る直線
まずは高校数学の内容から思い出してみましょう。図2のような2点を通る直線はどのように求めるか覚えていますか?
このように解きます。
まず、仮の線を「y = ax + b」と置く。
点A (1,1) から、「1 = a + b」が成り立つ【1】。
点B (2,2) から、「2 = 2a + b」が成り立つ【2】。
ここで、【1】から、「a = 1 - b」を?に代入すると、「b = 0」となる【3】。
【3】を【1】に代入すると、「a = 1」となる。
よって、点A、点Bを通る直線は、「y = x」となる。
これは比較的簡単ですね。
3点ある場合(直線的ではない)どうする?
では図3のような3点がある場合に、「全ての点の近くを通る線を求めよ」といわれたら、どのような線が適切でしょうか?
問いをもう少し具体化します。仮の線を「y = ax + b」とすると、先ほどのようにa,bの値が決まれば線が決定します。
従って、「どのような線を描くか?」=「a,bの値はいくつか?」ということになります。それでは、a,bはどのように求めるのでしょうか?
求める方法の一つに「最小二乗法」があります。
最小二乗法は“誤差の2乗”を“最小”にする方法
最小二乗法を使って図3の線を求めます。まずは、線と各点の距離を考えてみましょう。
- da = 1 - ( a + b)
- db = 2 - (2a + b)
- dc = 1 - (2a + b)
各点と線の距離はこのように表現できます。
ここで、「全ての点の近くを通る線」というのは上記1と2と3が全体的に最も小さくなるような線ということが分かってきます。では、1と2と3の“合計”が小さくなればよいのでしょうか? 実はそれだと不都合が出てきます。その理由を知るために次のケースを計算してみましょう。
da + db + dc = -2 + 2 + 0 = 0
なんと、全ての点を通っているわけではないのに、0になってしまいました。
このように、単に合計してしまうと線より上の点と下の点で互いに打ち消し合ってしまいます。これでは線の良しあしを正しく評価できません。では、どうするかというと、各距離を2乗します。
- da2 = (1 - a - b)2
- db2 = (2 - 2a - b)2
- dc2 = (1 - 2a - b)2
こうすることで、点の上下で距離を打ち消すことはなくなるので、安心して合計できます。
SSE = 6 + 9a2 + 3b2 - 14a - 8b + 10ab
ようやく出来上がった1と2と3の2乗の合計は、「残差平方和(SSE:Sum of Squared Error)」といいます。次のステップでは、この二乗誤差を最小にするようなa,bを求めます。
最適なa,bはいくつ?
先ほど算出した二乗誤差の値に注目します。二乗誤差はa,bによって値が決まることが分かります。つまり、a,bの「関数」になっていることが分かります。補足すると、デタラメに大きな値をa,bに代入したならばSSEの値もデタラメに大きくなり、逆に適切な値をa,bに代入するとSSEは小さくなるということです。
従って、SSEを“最小”にするa,bは「微分」を用いれば求めることができるのではないでしょうか。求める方法は下記の通りです。
これを詳しく説明しても退屈だと思います。本当にこのa,bの値が最適な値なのか、Pythonのプログラムで確認してみましょう。
import matplotlib.pyplot as plt
# データの作成
data = [
["A",1,1],
["B",2,2],
["C",2,1]
]
# y=ax+b
f = lambda x: a*x + b
# SE算出
get_error = lambda x,y: (y - f(x))**2
# aの検証
b = 0.5
res = list()
for a in range(0, 11):
a = a/10
SSE = sum([get_error(r[1], r[2]) for r in data])
res.append([a,SSE])
plt.scatter(x=a, y=SSE, c="red")
plt.xlabel("a")
plt.ylabel("SSE")
plt.show()
# bの検証
a = 0.5
res = list()
for b in range(0, 11):
b = b/10
SSE = sum([get_error(r[1], r[2]) for r in data])
res.append([b,SSE])
plt.scatter(x=b, y=SSE, c="red")
plt.xlabel("b")
plt.ylabel("SSE")
plt.show()
確かに、SSEを最小にするa,bはそれぞれ0.5,0.5で正しそうです。
単回帰分析、重回帰分析への拡張
ここからは現実にありそうなサンプルデータを使って説明します。図1の散布図を再度見てみましょう。
横軸をx、縦軸をyとしてこの図を眺めてみます。この場合、図3の3点の場合と何が違うでしょうか? それは点の数です。むしろ点の数以外は何も変わりません。
よって、図1のような単回帰分析はどのように行われているかというと、前述したa,bを求める方法と全く同様なのです。おさらいしましょう。
- y = ax + bを仮定する
- SSEを求める
- 微分によってSSEを最小にするa,bを求める
いかがでしょうか。これまでの「ポチっとボタンを押すと引かれていた線」の裏ではこのようなことが行われていたのです。
では、重回帰分析はどうでしょうか? アイスの販売個数に対する重回帰分析なら、下記が想定できるでしょう。
アイスの販売個数 = a気温 + b湿度 + c
これを求める場合のステップは下記の通りです。
- y = ax1 + bx2 + cを仮定する。
- SSEを求める。
- 微分によってSSEを最小にするa,b,cを求める。
このように、実は微分の回数が増えただけなのです。
ここまで単回帰/重回帰分析の中身を解説してきました。一般的にxxx分析と聞くと、「何やら難しいことをやっている」と思う方もいますが、一つ一つ解き明かしていけば、このようにシンプルなことでもあるのです。
まとめ
- 最小二乗法は、誤差の“2乗”を“最小”にする係数を求める手法
- 単回帰分析も重回帰分析も中の処理は同様に「最小二乗法」が行われている
今回学んだ単回帰/重回帰分析は最もシンプルで古典的な分析手法ですが、その扱いやすさ、解釈のしやすさから今でも多くの現場で使用されています。中身を理解することは、これからの学習に大いに応用できるので、しっかり押さえておきましょう。
関連記事
![[AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する](https://image.itmedia.co.jp/ait/articles/2006/04/news013.jpg) [AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する
[AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する
微分の考え方と計算方法を理解したら、次は微分の公式を押さえて活用してみよう。幾つかの公式を紹介し、応用例として回帰分析を行うための最小二乗法について基本的な考え方を見ていく。![[AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する](https://image.itmedia.co.jp/ait/articles/2007/14/news021.jpg) [AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する
[AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する
「偏微分」って何? いかにも難しそうな名前だが、微分を理解していれば意外に簡単。前回までの知識を踏まえて、今回は偏微分の意味と計算方法を理解しよう。![[AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する](https://image.itmedia.co.jp/ait/articles/2007/28/news014.jpg) [AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する
[AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する
これまでに見てきた、説明変数が1つだけの回帰分析と偏微分の基本知識を踏まえて、複数の説明変数がある重回帰分析を行うための基本的な方法を理解しよう。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

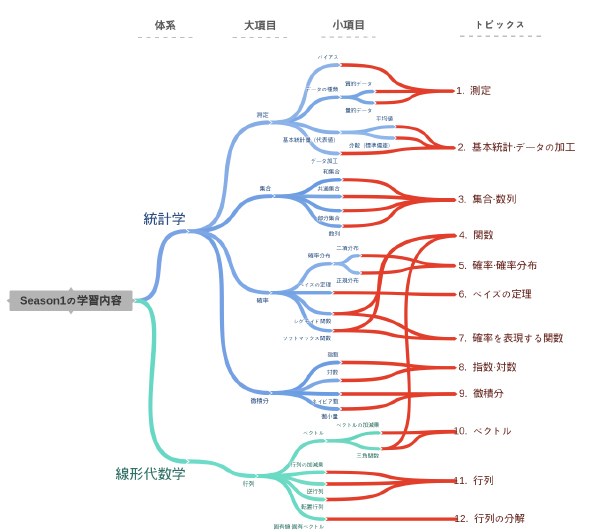 Season1基礎編の学習範囲(
Season1基礎編の学習範囲(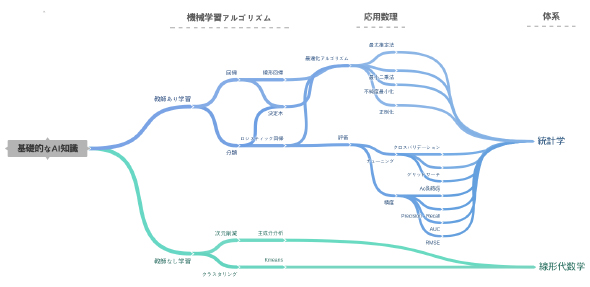 Season2応用編の学習範囲(
Season2応用編の学習範囲(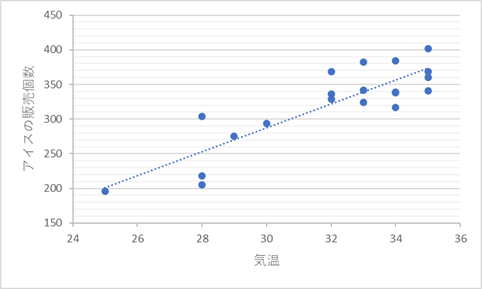 図1
図1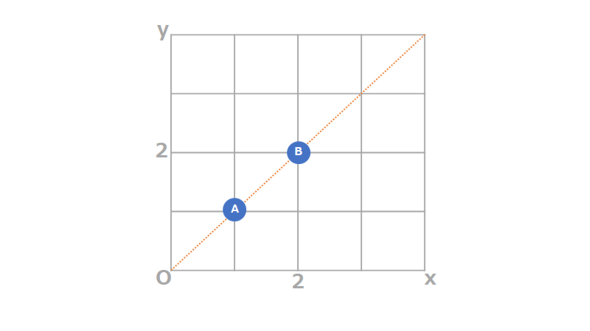 図2
図2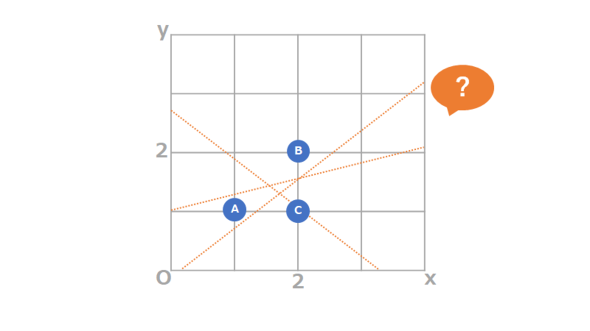 図3
図3 図4
図4 図5
図5





