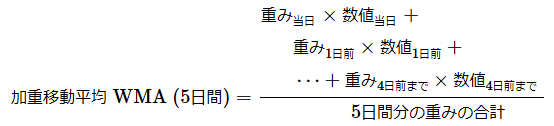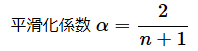移動平均(Moving Average)とは? SMA/WMA/EMAの違い:AI・機械学習の用語辞典
用語「移動平均」について説明。時系列データ(例: 株価)を平滑化すること、具体的には一定期間(例:5日間)の平均値を計算することをデータポイントごとに繰り返し、計算後の一連の平均値を線でつなぐこと(移動平均線)。データの長期的な傾向や短期的な動きを把握するのに役立つ。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
金融分野や数学/統計学/機械学習における移動平均(Moving Average)とは、時系列データ(例えば毎日の株価データ)の変動を平滑化(=なだらかに)することで、データの傾向や動きを見やすくする方法である。
具体的には、計算対象となる1つのデータポイント(例:ある1日の株価)に対して「特定の期間分のデータポイント(例:過去5日間分の株価)の平均値」を計算する。そして、次のデータポイント(例:次の日)に1つ移動して、再び新しい平均値を計算する、という過程を後続のデータポイントでも繰り返す。このようにして得られる一連の平均値を線でつなぐことで、平滑化された変動(例:5日間平均の株価の動き)を可視化できる。これにより、例えば「この期間は株価が上昇傾向にある」といった長期的な傾向が捉えやすくなるというわけだ。ちなみに、つながれた線は移動平均線と呼ばれる。
移動平均には、幾つかの種類がある。一般的には、「移動平均」と言えば単純移動平均(SMA:Simple Moving Average)を表すが、他にも加重移動平均(WMA:Weighted Moving Average)や指数移動平均(EMA:Exponential Moving Average)などがよく使われている。この他にも修正移動平均(MMA:Modified Moving Average)や三角移動平均(TMA:Triangular Moving Average)などの計算方式が存在するが、これらは特定の応用や研究の文脈で主に使われるため、本稿では説明を割愛する。
以下では、SMA/WMA/EMAの計算方法と特徴について説明した後で、それらの使い分け方針をまとめる。最後に移動平均全般の用例についてもまとめる。
SMA(単純移動平均)の計算方法と特徴
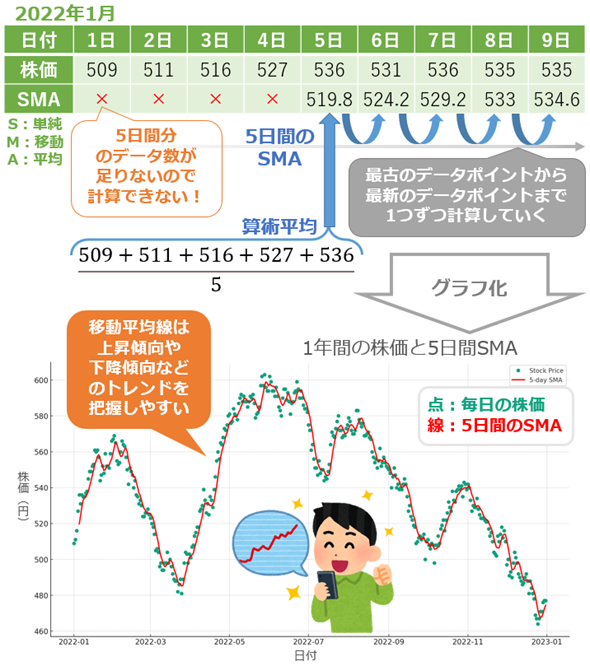
SMAの計算方法は、特定の期間に対する算術平均となる。算術平均(Arithmetic Mean)とは、データの各数値(xiは、データポイントである数値1, 数値2, ..., 数値nのいずれかの数値)を全て足した合計値をデータ数(n)で割ることである(相加平均とも呼ばれる)。よって例えば5日間のSMAの計算式は次のようになる。
また、5日間の5をnという変数に置き換えると、次のようにより汎用(はんよう)的に使える一般化された公式となる。これは算術平均と全く同じ式である。
この計算式は1つのデータポイントに対するもので、同様の計算を後続の各データポイントに対しても行っていく必要がある。SMAを計算する際には、通常、最古(=最初)のデータポイントから最新(=最後)のデータポイントに向かって進むことになる。ただし、特定の期間のSMAを計算するためには、その期間分のデータポイントが必要だ。例えば、5日間のSMAを計算する場合、「過去」5日間分のデータが必要になるため、データセットの最初にある4日間の各データポイントではSMAを計算しようにもデータ数が足りないことになる。このため、最初の4日間はSMAが計算できないことに注意が必要である。
SMAの特徴は、特定の期間(例:5日間)における各データポイントを均等に扱うことで、データの動き(傾向の変化)をバランス良く安定して捉えられることだ。
WMA(加重移動平均)の計算方法と特徴
WMAの計算方法は、特定の期間に対する加重平均である。加重平均(Weighted Mean)とは、データの各数値に重み(wiは、重み1, 重み2, ..., 重みnのいずれかの数値)を乗じたものを全て足し合わせ、それを重みの合計で割ることである。よって例えば、5日間のWMAの計算式は次のようになる。なお、各「重み」をどのように決定するかについては後述する。
また、5日間の5をnという変数に置き換えると、次のようにより汎用的に使える一般化された公式となる。これは加重平均と全く同じ式である。
この計算式は1つのデータポイントに対するもので、同様の計算を後続の各データポイントに対しても行っていく必要がある。WMAを計算する際には、通常、最古のデータポイントから最新のデータポイントに向かって進むことになる。従って、例えば5日間のWMAを計算する場合、最初の4日間の各データポイントではデータ数が足りないためWMAを計算できないことに注意してほしい。
WMAの「重み」は、特定の期間(例:5日間)における最新のデータポイント(例:当日)に対しては大きく、それより過去のデータポイント(例:1日前、2日前、3日前、4日前)に遠ざかるにつれ徐々に小さくしていくのが一般的だ。その重みを決定する代表的な手法には以下のものがある。
- 「線形的」な重み決定: 特定の期間における最新のデータポイントの重みから1ずつ線形的に減らす手法。例えば5日間のWMAの場合、当日が5で、1日前が4、2日前が3、3日前が2、4日前が1と減らしていく。重みの合計が1.0になるようスケール調整する場合もある。
- 「指数的」な重み決定: 後述のEMA(指数移動平均)に近い考え方で、特定の期間における最新のデータポイントの重みから指数関数的に減らす手法。線形的な場合よりも、最新のものはより大きな重みになり、過去になるほどより小さな重みになる。最新の情報に非常に敏感なWMAを作成できる。
- 「カスタム」重み決定: データ分析者が重みを独自に定義する。特定のデータポイントに特別な重要性を持たせたい場合に使う。
WMAの特徴は、特定の期間(例:5日間)における最新のデータポイントに大きな重みを置くことで、直近のデータの動き(傾向の変化)に敏感に反応できることだ。
EMA(指数移動平均)の計算方法と特徴
EMA(Exponential Moving Average:指数移動平均)は、指数平滑移動平均(Exponentially Smoothed Moving Average)とも呼ばれることも多い。また、指数加重移動平均(EWMA:Exponentially Weighted Moving Average)という呼び方もある。
EMAの計算方法は、現在計算対象としているデータポイント(=現在のDP)に定数α(アルファ、後述)を乗じた値と、1つ前のデータポイント(=1つ前のDP)に対するEMA値に1−αを乗じた値とを合計することである。数式で表現すると、次のようになる。
ちなみに、この式は次のように変形することもできる(※以下の説明では、この数式ではなく、上の数式を参照してほしい)。
EMAを計算する際には、通常、最古のデータポイントから最新のデータポイントに向かって進むことになる。最古のデータポイントには、「1つ前のDP」が存在しないため、通常のEMA計算はせずに、最古のデータポイントの数値そのものをEMAの初期値として用いればよい。もし最古のデータポイントでも、特定の期間に対する算術平均(つまりSMAと同じ計算)が可能な場合は、その算術平均値をEMAの初期値として用いればよい。
上記の数式で数値への「重み(Weight)」付けに使われている定数αは、平滑化係数と呼ばれる。その数式の定義は以下の通りだ。nは特定の期間を表す。
例えば特定の期間が「5日間」(n=5)のEMAを計算する場合は、次のように平滑化係数αが求まる。
前述したEMAの数式には「1つ前のDP」が含まれているため、「現在のDP」までに計算してきた全てのEMAの内容が継承されるイメージとなる(「1つ前」の中にある、「1つ前」の中にある、「1つ前」の中……という形で、マトリョーシカ人形のような入れ子をイメージしてほしい)。ただし、最新のデータポイントから遠いデータポイントであればあるほど、その数値は指数関数的に小さな影響(=重み)しか持たないという特徴がある。
例えば5日間のEMAであれば、平滑化係数は1/3(3分の1)であるため、1−α=2/3(3分の2)が「1つ前のDP」に乗じる重みとなる。これに基づき、「現在のDP」〜「3つ前のDP」に対して乗算する「重み」の数値だけを計算すると、以下のようになる。
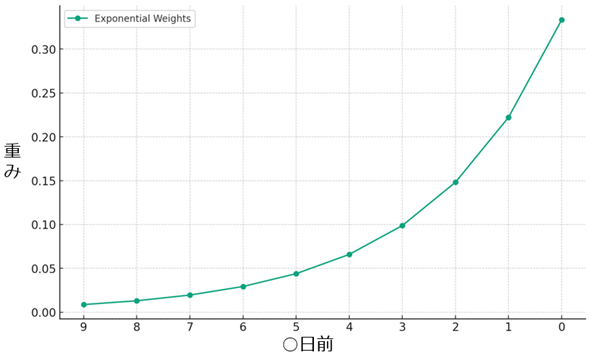
このようにデータポイントが過去であればあるほど指数関数的に、そのデータポイントに乗算する「重み」は減衰していく。図2は、5日間のEMAの場合に「現在(0日前)と、1〜9日前のDP」に乗じる「重み」をそれぞれ点でプロットし、それを線でつなげてグラフ化したものである。
図2を見ると、最新のデータポイントほど重要視し、過去のデータポイントほど指数関数的に軽視していくのが分かるだろう。
EMAの特徴は、特定の期間(例:5日間)における最新のデータポイントに指数関数的に大きな重みを置くことで、直近のデータの動き(傾向の変化)にWMAよりも大きくかつ早期に反応できることだ。
SMA/WMA/EMAの使い分け指針
SMA/WMA/EMAの特徴については、上記の各「計算方法と特徴」節の最後に1文でまとめた。これらを参考に、以下に使い分け方針をまとめておく。
- 長期的なデータのパターンや季節性をバランスよく安定して把握したい場合 → SMA(単純移動平均)
- 短期的なデータの動き(傾向の変化)を把握したい場合や、直近のデータの動きに敏感に反応させたい場合 → WMA(加重移動平均)
- 短期的なトレンド(=データの動き、傾向の変化)を検出したい場合や、データの急激な変化に大きく早期に反応させたい場合 → EMA(指数移動平均)
つまり、安定性では基本的に「SMA > WMA > EMA」となり、トレンドの追随しやすさは基本的に「EMA > WMA > SMA」となる。
移動平均の用例
最後に移動平均の代表的な利用場面について箇条書きで紹介する。
- トレンド把握: 移動平均の最も代表的な使い方。移動平均線が上昇傾向にあるか、下降傾向にあるかを目視で確認する。
- 取引シグナル: 株などの売買タイミングとして、「短期(例:5日間)移動平均線」が「中長期(例:25日間)移動平均線」を下から上に突き抜けるゴールデンクロスと、逆に上から下に突き抜けるデッドクロスが有名。
- ノイズ軽減: 移動平均はデータを平滑化するので、ノイズを減らせる。機械学習ではデータをスムージング(平滑化、ノイズ除去)して新たな特徴量を作る場合や、工学分野では信号処理のノイズ除去をする場合が考えられる。
Copyright© Digital Advantage Corp. All Rights Reserved.