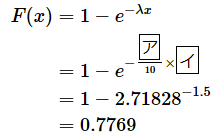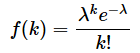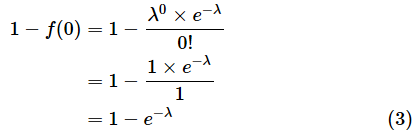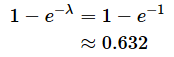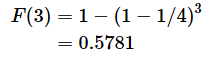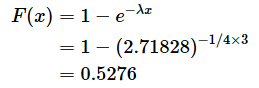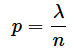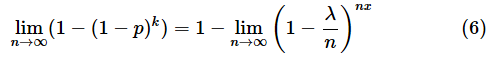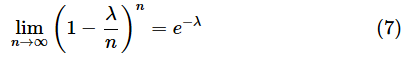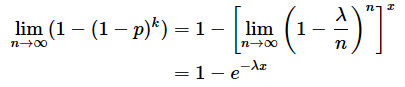［データ分析］指数分布～ 5分以内に次の顧客が到着する確率は？：やさしい確率分布

データ分析の初歩から学んでいく連載（確率分布編）の第10回。指数分布は待ち行列の分析などに使われる分布です。一定期間に起こる事象の数が分かっているときに、ある期間内にその事象が起こる確率が求められます。今回は具体例を基に、確率を求めたり、指数分布の確率密度関数や累積分布関数の形を見ていきます。

» 2024年11月07日 05時00分公開

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第10回です。前回は、分散の比に関連する分布として、F分布を取り上げました。今回は待ち行列の分析などに使われる指数分布について、その特徴や意味を基本から解き明かし、確率密度関数／累積分布関数の求め方、利用例などを見ていきます。

一定時間内に顧客が来る確率は？～指数分布の利用

　指数分布は、一定の時間内に事象（何らかの出来事）が何回か起こることが分かっているときに、ある時間間隔でその事象が起こる確率を表す分布です。これは、具体的な例で説明した方が分かりやすいでしょう。例えば、ある店舗で、顧客が10分当たり3人来ることが分かっている場合、次の5分間に顧客が来る確率を求める、といった場合に使われます（図1）。

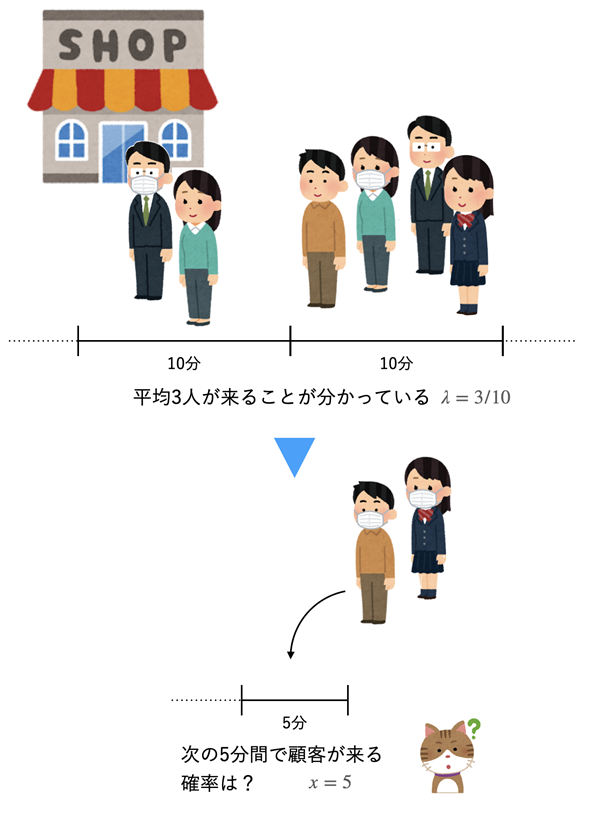図1　ある時間内に顧客が来る確率を知りたい！
単位時間に事象が起こる回数λが分かっているとき、目的の時間間隔xの間にその事象が起こる確率を求めるのに指数分布（の累積分布関数）が使える。顧客が10分当たり3人来る場合、単位時間は「分」なので、λの値は3/10。目的の時間間隔が5分ならx＝5となる。

　指数分布の確率変数xは目的の時間間隔です。単位時間内で事象が起こる回数をλ（ラムダ）とすると、指数分布の確率密度関数と累積分布関数は以下の式で定義されます。eは自然対数の底（＝2.71828...）です。

◆ 指数分布の確率密度関数

◆ 指数分布の累積分布関数

　母数はλだけなので、λの値が決まると関数の形が決まります。指数分布の累積分布関数を使えば、目的の時間内に次の顧客が来る確率が求められるので、図1の例で計算してみましょう。

　単位時間は「分」とします。10分当たり3人の顧客が来るということは、1分当たりλ＝3/10人が来るということです。目的の時間間隔は5分なので、x＝5です。（2）式に当てはめてみましょう。簡単な穴埋め問題にしてあります。オレンジ色の部分をタップまたはクリックすると答えが表示されます。

　答え：ア＝　3　、イ＝　5　

　なお、指数分布の累積分布関数は、目的の時間内に次の顧客がちょうど1人来る確率ではないことに注意してください。顧客は何人来てもいいので、顧客が0人ではない（＝少なくとも1人来る）確率であると考えられます。

　指数分布が問題としているのは、何人の顧客が来るかということではなく、あくまでも、次の顧客が来るのが目的の時間内である確率です（目的の時間間隔が指数分布の確率変数であることからも明らかです）。

　指数分布は一定時間内に機械が故障する確率を求めたり、一定期間内に株価が暴落する確率を求めたりするなど、さまざまな場面で応用されます。

　では、次に指数分布の確率密度関数と累積分布関数を可視化してみましょう。

指数分布ってどんな感じの分布（1）～確率密度関数を可視化してみよう

　指数分布の確率密度関数や累積分布関数を可視化するには（1）式や（2）式をそのまま使ってもいいですが、ExcelのEXPON.DIST関数を使うのが簡単です。EXPON.DIST関数の形式を見ておきましょう。

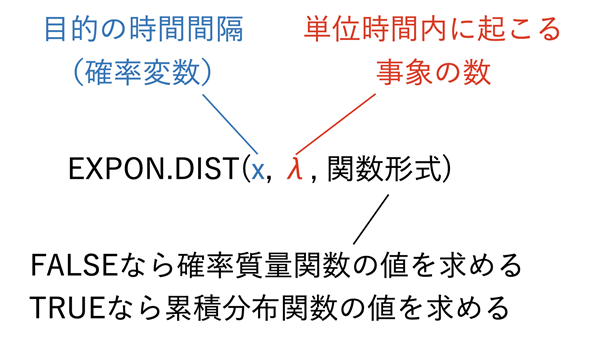図2　EXPON.DIST関数に指定する引数
EXPON.DIST関数には、目的の時間間隔xと、単位時間内で事象が起こる回数λを指定する。関数形式についてはこれまでの連載で見てきた関数と同様、FALSEを指定すれば確率密度関数の値が、TRUEを指定すれば累積分布関数の値が求められる。

　まず、確率密度関数から見ていきます。図3は、幾つかのλの値を想定し、x＝0.0～15.0までの確率密度関数の値をプロットしたものです。表の作成手順は図の後に記しておきます。

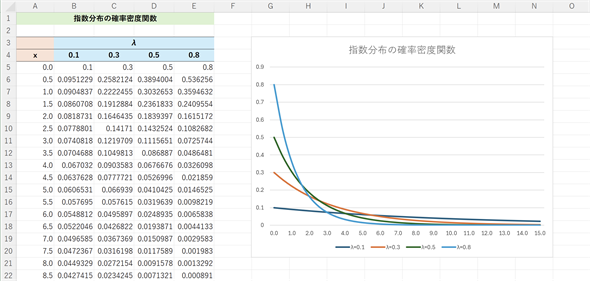図3　指数分布の確率密度関数の例
λは0.1, 0.3, 0.5, 0.8とし、x＝0.0～15.0までの確率密度関数の値を0.5刻みで求め、グラフを描いてみた。xと表記されているA列の値が確率変数。B～E列はそれぞれのλに対する確率密度関数の値。

　確率密度関数の値を求めるための手順は以下の通りです。可視化については単に折れ線グラフを描くだけなので、関数の入力にのみ焦点を当てることにします。グラフ作成の手順についてはサンプルファイル内に掲載しておきます。

　サンプルファイルをこちらからダウンロードし、［指数分布］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］－［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。なお、（1）式の通りに計算した例も［指数分布（定義通りに作成）］ワークシートに含めてあります。

◆ Excelでの操作方法

セルB5に=EXPON.DIST(A5:A35,B4:E4,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB5～E35）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

セルB5に=ARRAYFORMULA(EXPON.DIST(A5:A35,B4:E4,FALSE))と入力する

● グラフの作成方法

サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

指数分布ってどんな感じの分布（2）～累積分布関数を可視化してみよう

　続いて、累積分布関数です。こちらは、λ＝0.3の例だけを見ておきます（図4）。［指数分布累積］ワークシートを開いて、図の後の手順で試してみてください。

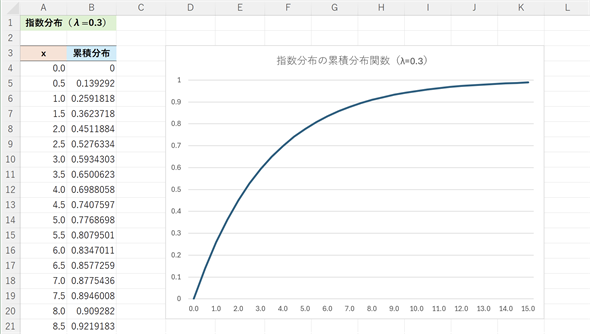図4　指数分布の累積分布関数の例
λ＝0.3とし、x＝0.0～15.0までの累積分布関数の値を0.5刻みで求め、グラフを描いてみた。最初に見た顧客の例（λ＝0.3, x＝5.0の値）は、セルB14で求められている（0.7769となっている）。

　累積分布関数の値を求めるための手順は以下の通りです。ここでも、関数の入力にのみ焦点を当てることとし、グラフ作成の手順についてはサンプルファイル内に掲載しておきます。

◆ Excelでの操作方法

セルB4に=EXPON.DIST(A4:A34,0.3,TRUE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB4～B34）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

セルB4に=ARRAYFORMULA(EXPON.DIST(A4:A34,0.3,FALSE))と入力する

● グラフの作成方法

サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

　指数分布では、確率変数を求めるための計算などもなく、また、累積分布関数が直接応用に結び付くので、比較的すんなりと理解できるのではないかと思います。ここからは、少し発展的なお話としてポアソン分布との関係や幾何分布との関係を見てみます。実用的には知らなくてもあまり問題がないので、数式が苦手な方は、最後の「この記事で取り上げた関数の形式」を確認して、今回はお開きとしてもらっても構いません。

コラム　指数分布とポアソン分布の関係

　指数分布のお話を読みながら、何か前にやったことがあるような……という既視感にとらわれた方もいるのではないでしょうか。この連載の第4回で紹介したポアソン分布の確率質量関数に似ていますよね。100年に1人の天才が今後100年間に何人か現れる確率を求めるのにポアソン分布の確率密度関数を使いました。具体例で比較してみましょう。

ポアソン分布の確率質量関数の例： 100年に1人の天才が、今後100年間にk人現れる確率はいくらか
指数分布の累積分布関数の例： 100年に1人の天才が、期間x内に少なくとも1人現れる確率はいくらか

　一般化するために、100年を単位時間として書き直してみましょう。単位時間当たりに起こる事象の数はλと表せます（ここではλ＝1です）。

ポアソン分布の確率質量関数の例：単位時間にλ人の天才が、単位時間内にk人現れる確率はいくらか
指数分布の累積分布関数の例：単位時間にλ人の天才が、期間x内に少なくとも1人現れる確率はいくらか

　上の箇条書きで太字にした部分、つまり、ポアソン分布の事象の数をk＝1とし、指数分布の期間を単位時間x＝1とすれば、どちらもほとんど同じです。が、重要な違いがあります。

　それは、ポアソン分布ではk＝1人現れる確率はいくらか、ということであるのに対し、指数分布では少なくとも1人現れる確率はいくらか、つまり0人でない確率はいくらかということです。……ということは、ポアソン分布でk＝1の確率ではなく、k＝0でない確率を求めれば、指数分布の累積分布関数と同じ値になるはずですね。

　ポアソン分布の確率質量関数は以下の式で定義されます。

　k＝0でない確率は1－f(0)なので、

　一方、指数分布の累積分布関数は以下の通りでした。

　x＝1を代入すると、

となり、（3）式と（4）式がちゃんと一致します。上の例では、100年を単位時間として（100年を1として）、その期間に1人の天才が現れるのでλ＝1です。その場合、今後100年間に少なくとも1人の天才が現れる確率は、

となります。

　というわけで、λが等しく、xが単位時間と等しい場合、次の単位時間内に少なくとも1回の事象が起こる確率は、ポアソン分布の確率質量関数を使っても、指数分布の累積分布関数を使っても求められるというわけです。なお、上の事例をEXPON.DIST関数とPOISSION.DIST関数で計算した例、定義に従って計算した例の両方を［指数分布とポアソン分布］ワークシートに含めてあるので、興味のある方はご参照ください。

コラム　指数分布と幾何分布の関係

　既視感と言えば、指数分布は第5回で紹介した幾何分布の累積分布関数にも似ているような気がしませんか。幾何分布の累積分布関数F(k)は、k回目までに目的の事象が起こる確率を表します。

　連載の第5回では、当選確率がp＝1/4のライブチケットの抽選で、k＝3回目に当選する確率を求めるのに幾何分布の確率質量関数を利用しました。k＝3回目までに当選する確率を求めるなら、幾何分布の累積分布関数を利用すればいいですね。（5）式にpとkの値を代入すると、

となります。

　上の例は、指数分布ではλ＝1/4、x＝3となります（4回に1回当選する抽選に、3回のうち少なくとも1回当選する確率ということですね）。既に見た、指数関数の累積分布関数の（2）式に当てはめると、

となります。違いが生じるのは、指数分布が、幾何分布の回数を細かく分けた場合の近似値となっているからです。ここでは回数をあまり細かく分けていないので、違いが大きくなっていますが、pやλを小さくし、kやxを大きくすれば、ほぼ等しくなります。

　上の事例をEXPON.DIST関数とNEGBINOM.DIST関数で計算した例、定義に従って計算した例の両方を［指数分布と幾何分布］ワークシートに含めてあるので、興味のある方はご参照ください。例えば、pやλの値として0.01、kやxの値として100などを指定すると、結果はほぼ一致します。