クラウドサービスに最適な暗号方式とは？――暗号化したまま計算する「準同型暗号」：クラウド時代の暗号化技術論（4）（2/2 ページ）

[光成滋生，＠IT]

完全準同型暗号

　前節で紹介したのは加法準同型暗号でした。これと同様に、暗号化したまま乗算ができる「乗法準同型暗号」というものもあります。しかし、「加法と乗法の両方を同時に実現する」準同型暗号は長らく実現していませんでした。そのような暗号を「完全準同型暗号（FHE：Fully HE）」といいます。

　0と1からなる「2で割った余りの世界」では、乗算は論理積（AND）、加法は排他的論理和（XOR）に相当し、ANDとXORの組み合わせだけで任意の演算を構成できることが知られています。そのため、加法と乗算の両方ができると、“完全”準同型暗号といわれるのです。式で書くと任意の関数fに対して、

　f(Enc(m))=Enc(f(m))

と表現できます。

表1 0と1のANDとXOR

AND（×）	0	1
0	0	0
1	0	1

XOR（＋）	0	1
0	0	1
1	1	0

　2009年、暗号研究者たちの夢であったこのFHEを、クレイグ・ジェントリー（Craig Gentry）氏が初めて実現しました。ジェントリー氏の作ったFHEは、鍵や暗号文が数百MバイトからGバイト単位と巨大で、実用的とはとても呼べませんでしたが、このブレークスルー以降、研究は急速に進んでいます。とはいえ、任意回の加法と乗算が可能という性質を実現するのはなかなか大変で、気軽に利用できるようになるのはまだしばらく先でしょう。

　ところで、準同型暗号の応用例を考えると、分散、相関、ベクトルの内積などを暗号化したまま処理したい場面が多いことが分かりました。これらの計算は、以下のように、2個の数値を一度だけ乗算したものを足し込むという操作で表現できます。

　(a₁,…,a_n)・(b₁,…,b_n)=a₁・b₁+a₂・b₂+…+a_n・b_n

　そこで、これらの処理だけはできるような制限付きの「ちょっとだけ準同型暗号（SHE：Somewhat HE）」にターゲットを絞った研究もされています。表2は各暗号において可能な演算と性能をまとめたものです。可能な乗算回数が増えるほど、できる計算の種類は増えますが、処理性能が悪くなります。

表2 準同型暗号の比較

	加算回数	乗算回数	処理性能	計算
従来の暗号	×	×	◎	暗号化のみ
加法HE	任意回	×	○	平均など
SHE	十分な回数	数回	△	分散、内積など
FHE	任意回	任意回	×	任意の演算

　SHEやFHEの実用化を目指した研究としては、例えば次のようなものがあります（各大学、研究所が活発に研究していますので、ここで挙げたものはそのごく一部です）。

表3 SHE、FHEに関する近年の研究例

発表年	組織	概要
2013	富士通研究所	『世界初！暗号化したまま統計計算や生体認証などを可能にする準同型暗号の高速化技術を開発』 指紋や静脈データといった生体認証の照合に必要な内積演算を高速化しています。複数の企業間での医療や生化学データなどの機密情報のデータ分析にも利用できるだろうとのことです。 http://pr.fujitsu.com/jp/news/2013/08/28.html
2014	NTTセキュアプラットフォーム研究所	『整数上完全準同型暗号の研究』 アルゴリズムを改良した高速なFHEを提案、実装しています。例えば、FHEを使用して作ったAESの回路に、FHEで暗号化したデータを入力し、「FHEで暗号化したデータをさらにAESで暗号化したもの」を出力するということも、数十秒程度で可能だそうです。 http://www.ntt.co.jp/journal/1403/files/jn201403071.pdf
2015	情報通信研究機構（NICT）	『暗号化状態でセキュリティレベルの更新と演算の両方ができる準同型暗号方式を開発』 暗号化したままデータのセキュリティレベルを更新することを可能にしています。従来、データの暗号方式を更新するには、データを一度ダウンロードして復号し、新しい方式で暗号化し直してからアップロードする必要がありました。NICTの手法では、データを暗号化したまま、クラウド上で鍵長を長く暗号化し直せるとのことです。 http://www.nict.go.jp/press/2015/01/19-1.html

「格子暗号」――SHE、FHEの実現方法

　今のところ、SHEやFHEは「格子」を使って実現されるものが主流です。格子とは、障子やジャングルジムなどのように空間を等間隔に区切ったものです（直角である必要はありません）。

図3 2次元格子と誤差付きベクトルの加算

　非常に大ざっぱで厳密ではないのですが、概要を説明します。格子を使った準同型暗号は、暗号文を格子点の上で表現するときに誤差を付与します。xを平文の情報を正しく持つきれいな値、ϵを誤差とすると、暗号文はx+ϵの形をしています。秘密鍵を持っている人は誤差を取り除いて元の平文を復号できますが、秘密鍵を知らない人は誤差を取り除くことが困難で、解読できません。

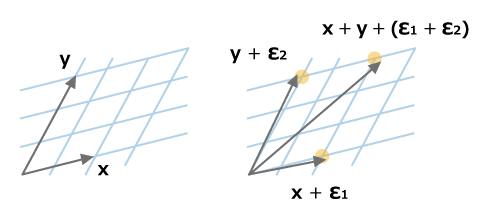
　さて、2個の暗号文x+ϵ₁、y+ϵ₂を用意して、これらを足します。

　(x+ϵ₁)+(y+ϵ₂)=(x+y)+(ϵ₁+ϵ₂)

　これは正しい値(x+y)と誤差(ϵ₁+ϵ₂)の形をしています。そこで秘密鍵を使うと、x+yを取り出せます。これが加法準同型暗号に相当します。

　次に、これらの暗号文を掛けてみます。

　(x+ϵ₁)(y+ϵ₂)=(xy)+(ϵ₁y+ϵ₂x+ϵ₁ϵ₂)

　ϵ₁、ϵ₂がx、yに比べて小さければ、これも正しい値(xy)と誤差の和という形です。秘密鍵を使えばxyを取り出せます。これが乗法準同型暗号に相当します。加法と乗法ができるので完全準同型を構成できるというわけです。

　この方式は、何度も計算すると誤差が蓄積してうまく復号できなくなります。そのため、演算回数に制約が発生します。その制約のまま使うのがSHE、さまざまな手法を用いて制約を取り払ったものがFHEです。

　最後に、量子コンピューターとの関係についても紹介します。RSAや楕円曲線を使った暗号は、将来量子コンピューターが登場すると、効率のよいアルゴリズムを用いて破られるといわれています。しかし格子暗号は、量子コンピューターに対しても安全とされています。そのため格子暗号は、完全準同型を実現できるというだけでなく、耐量子コンピューター暗号としても注目されているのです。

今回のまとめ：

• 準同型暗号は暗号化したまま計算できるためクラウドと相性がよい。
• 楕円曲線を用いて加法準同型暗号、格子を用いて完全準同型暗号を構築できる。
• 格子暗号は耐量子コンピューター暗号としても注目されている。

参考文献――より詳しく学びたい人のために：

準同型暗号や格子暗号を一般向けに解説したテキストはまだあまりありません。Web上で閲覧できるものや書籍として入手できるものとしては、以下のようなものがあります。

• 『クラウドを支えるこれからの暗号技術』（光成滋生）
• 『イデアル格子暗号入門』（有田正剛）
• 『量子コンピューターの解読に耐えうる暗号アルゴリズム――「格子暗号」の最新動向』
  （清藤武暢、青野良範、四方順司）

「クラウド時代の暗号化技術論」バックナンバー

• まだまだ広く深い、暗号の世界――匿名認証や電子投票に利用される「ブラインド署名」「グループ署名」「ゼロ知識証明」
• マイナンバーの漏えい対策にも利用される「検索可能暗号」とは――安全性と利便性の両立を目指す注目の暗号技術
• 動画配信サービスにも応用できる暗号とは――アクセス権を制御する「属性ベース暗号」
• メールアドレスを公開鍵にする――「ペアリング」とその応用例
• クラウドサービスに最適な暗号方式とは？――暗号化したまま計算する「準同型暗号」
• 鍵が漏れることも想定せよ――クラウド時代における「楕円曲線暗号」の必然性
• “安全な暗号”とは何か――「強秘匿性」「頑強性」という概念
• 重要なデータを守るため、もう一度暗号化技術をおさらいしよう

光成滋生（みつなり　しげお）

サイボウズ・ラボ株式会社

　サイボウズ・ラボ株式会社にてセキュリティとインフラ周りの研究開発に携わる。「数論アルゴリズムとその応用」研究部会（JANT）幹事。

• 2004年放送型暗号の実装でIPA未踏スーパークリエータ認定
• 2005年ストリーム暗号Toyocryptの解読で情報化月間推進会議議長表彰
• 2010年ベクトル分解問題についての論文で電子情報通信学会論文賞受賞
• 2015年 Microsoft MVPアワード Developer Securityを受賞

　近著に「応用数理ハンドブック」（朝倉書店、2013：楕円曲線暗号、ペアリング暗号の項目担当）、「クラウドを支えるこれからの暗号技術」（秀和システム、2015）がある。