数値と算術演算:Python入門(1/2 ページ)
Pythonはさまざまな種類の数値を扱える。今回は整数と浮動小数点数について簡単に見た後、それらを利用して四則演算などの操作を行ってみよう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
* 本稿は2019年4月9日に公開された記事を、Python 3.11.5で動作確認したものです(確認日:2023年9月11日)。
前回はPythonプログラムを構成する変数や文字列、関数といった基本要素を見た。今回はPythonで整数と実数(浮動小数点数)の計算をしながら、以下の要素について見ていくことにしよう。
Pythonで計算してみよう
コンピュータは「計算機」であり、Pythonは「計算機を操るためのプログラミング言語」なので、Pythonはもちろん計算にも使える。Pythonで扱える数値の種類には主に以下がある。
- 整数
- 実数
そこで「1+1」の計算をしてみよう。Jupyterのノートブックを開き(開き方は第1回を参照のこと)、セルに「1 + 1」と入力して、[Run]ボタンをクリックするだけだ。
ここで注意したいのは、「1」と「+」はどちらも「半角文字」である必要があることだ。それから「1」と「+」の間には空白文字を含めても構わない。上では含めている。このように、数値と記号などを区切ったり、コードを見やすくしたりするために空白文字を含めるのはPythonに限らず、多くのプログラミング言語で行われている。
今見たのは整数の加算だ。今度は実数で引き算(減算)をしてみよう。上と同様にして、セルに「1.0 - 1.0」と入力して実行ボタンをクリックしてみよう。
注目したいのは引き算の結果だ。「0.0」と表示されている。「1 - 1」の結果はどうなるだろう。
こちらの計算結果は「0」となっている。これらのことから想像できる人もいるだろうが、Pythonでは整数は「小数点なし」で表現され(当たり前だが)、実数は「小数点付き」で表現される。そして、Python内部ではこれらは違う種類のデータとして扱われている。その区別のことを「データ型」あるいは省略して「型」などと呼ぶ。
Pythonでは整数値は「int型」に属し、実数は「float型」に属する。「int」は整数を意味する「integer」を略したもので、「float」はPythonでは実数が「浮動小数点数」(floating point number)として表現されることに由来している。同様に、前回に見た文字列にも型があり、文字列はstr型に属する。こちらは文字列を意味する「string」に由来する型の名前だ。また、ある「型」に属する個々の値のことをPythonでは「オブジェクト」と呼ぶ。「1」はint型のオブジェクト、「1.0」はfloat型のオブジェクトである。
整数型/int型
今述べたように、整数はint型の値で小数点なしの数として表現される。
実際にint型の値であることは、Pythonの組み込み関数(Pythonが標準で提供している関数)のtype関数を使って調べられる。例えば、セルに「type(1)」と入力して、実行ボタンをクリックしてみよう。
type関数は引数に指定した値(オブジェクト)の型(type)が返される。上の例を見ると、確かに整数「1」というオブジェクトの型は「int」となっている。
ここまでに見てきた整数は全て「10進数」として表記されたものだが、Pythonでは加えて、2進数/8進数/16進数の数値としても記述できる。
- 2進数:先頭に「0b」を置き、その後に「0」と「1」で構成された2進数値を続ける
- 8進数:先頭に「0o」を置き、その後に「0」〜「7」で構成された8進数値を続ける
- 16進数:先頭に「0x」を置き、その後に「0」〜「9」「A」または「a」(10進数の「10」を表す)〜「F」または「f」(10進数の「15」を表す)で構成された16進数値を続ける
例えば、10進数の「253」は2進数では「11111101」と、8進数では「375」と、16進数では「FD」と表現できる。そこで、それぞれの表現に「0b」「0o」「0x」などを付けたものをセルに入力して、実行ボタンを押してみた結果を以下に示す(以下では16進数表記で大文字の「FD」ではなく「fd」という表記を使っている)。各セルの下には10進数の「253」が表示されているのが分かるはずだ。
普段は2進数/8進数/16進数の表記を使うことはあまりないかもしれないが、「ビット処理」と呼ばれる「2進数の各桁」を使って情報を処理する際などにこうした表現を使うこともあるだろう(2進数では各桁が0か1を示すので、これを使って何らかの「フラグ」のオン/オフを表現できる。プログラムで何らかの「フラグ」を大量に扱う場合には個別の変数にそれらのフラグのオン/オフを保存するのではなく、1つの整数値にそれらをまとめて保存すると便利なことがある)。
なお、数値を表記する際には間にアンダースコア「_」を挟み込んでもよい。桁数が多いときなどに、桁区切りのカンマ「,」の代わりに入れるものだと考えられる。例えば、10進数では3桁区切りでカンマを入れることでその値を見た目に理解しやすくなる。特に2進数は桁が多くなることがあるので、4桁ごとに「_」を入れるとコードが見やすくなるだろう。以下はその例だ。
ちなみに、「1」や「42」など、整数を「そのままの見た目」で表記したものを「整数リテラル」と呼ぶことがある。リテラル(literal)は「文字通りの」といった意味の言葉で、プログラムコード中に「文字通り」に表記された整数値や実数値(あるいは文字列値など)をそのように呼ぶ。
浮動小数点数型/float型
既に見たように、実数は「小数点付き」で表現される数値(オブジェクト)だ。小数点の後を省略して表記してもよい。例えば、「1.」はfloat型の「1.0」を意味する。以下を見てほしい。
最初のセルは「1.」の値を示したもので、次のセルはその型を調べたものだ。「1.」が実数の「1.0」で、その型が「float」であることを確認してほしい。
先ほど「floatは浮動小数点数(floating point number)に由来する」と述べたが、これは実数を表記する際の「7.73×102」のような記述に似たものだ。浮動小数点数は「仮数」「基数」「指数」の3つで構成される。例えば、今の例であれば仮数は「7.73」に、基数は「10」に、指数は「2」になる。
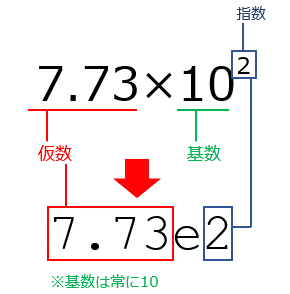
ただし、Pythonでは浮動小数点数リテラル(コード中に直接書いた浮動小数点数値)の基数は常に10となる(仮数部も10進数値として扱われる)。そして、これをPythonでは次のような構文で記述する。
「773.0」と「7.73e2」のいずれの表記を使っても、Pythonではそれがfloat型の値として扱われる。「e付きの表記法」では「仮数はそのまま」「指数をeの右に置く」というのがポイントだ(基数は10固定)。
幾つか例を見ながら、浮動小数点数に慣れてみよう。まず、マイナスの値はどうなるだろう。「-9876.5432」という値は、浮動小数点を使うと「-9.8765432×103」と書ける。ということは、これはPythonの「e付きの表記法」では「仮数はそのまま」「指数をeの右に置く」ことから、これは「-9.8765432e3」と書ける。なお、指数が正の値のときにはeの右に置く数値に明示的に「+」を付けてもよい。つまり、「-9.8765432e+3」のように書いても同じことになる。
「指数が正の値のとき」と今書いたが、指数は「負の値」となることもある。「0.0001234」のように、1より小さな値を浮動小数点を使って表すときにはそのようになる。「0.0001234」を浮動小数点表記にすると「1.234×10-4」となるので、e付きの表記方法ではこの値は「1.234e-4」となる。
これまでに出た数値を含めて、幾つかの例を以下の表にまとめる。
| 10進数の固定小数点表記 | 浮動小数点表記 | Pythonでの「e」付きの書き方 |
|---|---|---|
| 773.0 | 7.73×102 | 7.73e2 7.73e+2 |
| -9876.5432 | -9.8765432×103 | -9.8765432e3 -9.8765432e+3 |
| 0.0001234 | 1.234×10-4 | 1.234e-4 |
| -0.1234567 | -1.234567×10-1 | -1.234567e-1 |
| 987654321.012 | 9.87654321012×108 | 9.87654321012e8 9.87654321012e+8 |
| 浮動小数点数の例 | ||
先ほども述べたが、指数部が大きければ絶対値の大きな値を表現し、指数部が小さければ絶対値の小さな値(0に近い)値を表現することになる。どのくらいの範囲の数値を表現できるかどうかは、使用するPython環境にもよるが、多くの場合は次のような範囲になる。
- -1.7976931348623157×10308〜1.7976931348623157×10308
といっても、上の範囲を見ても、この値がどれくらいの値か分かりにくい。要するに「1.79769……」の小数点が300個以上右の桁に移動するということだ(途方もなく大きな値であることは分かるだろう)。一方、多くのPython環境で表現可能な最小の正の値は2.2250738585072014×10-308となる。これは、小数点以下に0が300個以上並んでから仮数に置いた「22507……」が続くということだ。なお、無限大を表す「inf」という値も扱える(「inf」は「infinity」の意味)。
浮動小数点数(float型)には「誤差」や「精度」(有効桁数)なども付きものであることは忘れないようにしよう。例えば、「0.1 + 1.6」という足し算の結果はどうなるだろう。普通に考えると「1.7」となる。
直観で得られる「1.7」ではなく「1.7000000000000002」となっている。これはコンピュータ内部での浮動小数点数の表現方法に起因するもので、避けることができない。ただし、「1.7×100」と「1.7000000000000002×100」の差は「0.0000000000000002」≒「2.0×10-16」であり、十分に「1.7」と同一視できるものと扱える(と考えるようにしよう)。
今見たように、浮動小数点数(float型)には誤差が付きものだ。だが、多くのPython環境では、浮動小数点数は15桁の精度(有効桁数)までは正確に表現できるようになっている。これだけの精度があれば、誤差は無視できる場面が多いはずだ。円周率は無限小数(無理数)だが、日常的には「3.14」とか「3.14159」とかと見なすのと似た感覚だ。
なお、10進数の浮動小数点数をより正確に取り扱うための機構として、Pythonにはdecimalモジュールがあるが、これについては本稿では取り上げない。興味のある方はPython公式サイトのドキュメント「decimal --- 十進固定及び浮動小数点数の算術演算」を参照されたい。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

![セルに「1 + 1」と入力して、[Run]ボタンをクリック](https://image.itmedia.co.jp/ait/articles/1904/09/di-pybasic0301.gif)

 実数の減算をしたところ
実数の減算をしたところ 「1 - 1」の計算結果
「1 - 1」の計算結果 type関数を使うと、引数に指定した値の型を調べられる
type関数を使うと、引数に指定した値の型を調べられる 10進数の「253」を2進数/8進数/16進数を使って表現
10進数の「253」を2進数/8進数/16進数を使って表現 桁区切りに「_」を入れたもの
桁区切りに「_」を入れたもの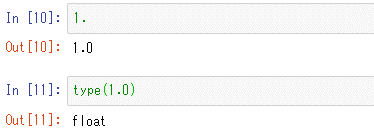 「1.」はfloat型の「1.0」
「1.」はfloat型の「1.0」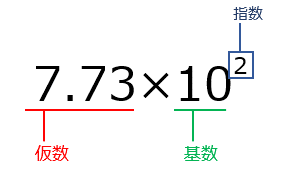
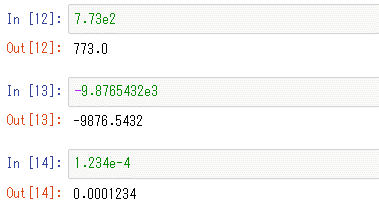 浮動小数点数の例
浮動小数点数の例 「0.1 + 1.6」は?
「0.1 + 1.6」は?



