[NumPy超入門]逆行列、行列式、固有値と固有ベクトルを計算してみよう:Pythonデータ処理入門
NumPyが提供するndarrayオブジェクトで行列を扱う際には、逆行列や行列式、行列の固有値と固有ベクトルが簡単に求められます。その基本を見ていきましょう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
連載概要
本連載はPythonについての知識を既にある程度は身に付けている方を対象として、Pythonでデータ処理を行う上で必須ともいえるNumPyやpandas、Matplotlibなどの各種ライブラリの基本的な使い方を学んでいくものです。そして、それらの使い方をある程度覚えた上で、それらを活用してデータ処理を行うための第一歩を踏み出すことを目的としています。
逆行列を求めるには
ある正方行列A(行数と列数が同じ行列)があったときに、Aとの行列積を計算すると単位行列(行列の左上から右下に向けた対角要素の値が1、他の要素の値が0となるような行列)となるような行列のことを逆行列と呼び、A-1と表記します。Iを単位行列とすると、A・A-1=A-1・A=Iとなるような行列のことです。ただし、全ての行列に逆行列が存在するわけではないことには注意が必要です(逆行列が存在する行列のことを正則行列と呼びます)。
以下に例を示しましょう。
import numpy as np
a = np.array([[1, 2], [3, 4]])
print(a)
# 出力結果:
#[[1 2]
# [3 4]]
ここでは2行2列の正方行列aを作成しています。この行列(2次元配列)には逆行列が存在します。2行2列の行列の逆行列は次の計算式で求められます。
上で作成した行列であれば、逆行列は次のようになります。
これを基に逆行列を作成したのが以下です。
inva = np.array([[-2, 1], [1.5, -0.5]])
print(inva)
# 出力結果:
#[[-2. 1. ]
# [ 1.5 -0.5]]
invaという名前にしたのは逆行列の英語表記である「inverse matrix」から頭の「inv」をもらったからです。では、invaがaの逆行列かどうかを確認してみましょう。これにはaとinvaの行列積を計算して、その結果が単位行列となるかどうかを見るだけです。ここではnumpy.dot関数を使っていますが、@演算子やnumpy.matmul関数を使っても同様です。
result = np.dot(a, inva)
print(result)
# 出力結果:
#[[1. 0.]
# [0. 1.]]
result = np.dot(inva, a)
print(result)
# 出力結果:
#[[1. 0.]
# [0. 1.]]
aとinvaの行列積、invaとaの行列積はどちらも単位行列となっていることが確認できました。よって、invaはaの逆行列(aはinvaの逆行列)であるということです。
上では逆行列を求める式から計算をしていましたが、NumPyでは逆行列をnp.linalg.inv関数で簡単に計算できます(しかも2行2列の行列に限らず任意の正則行列の逆行列を求められます)。引数は1つだけで、逆行列を求めたい行列(二次元配列)を与えます。以下はその例です。
inva = np.linalg.inv(a)
print(inva)
# 出力結果:
#[[-2. 1. ]
# [ 1.5 -0.5]]
出力結果を見ると分かるように先と同じ結果が得られたようです。では、ここでもaとinvaの行列積を計算してみましょう。ここでは@演算子を使ってみます。
result = a @ inva
print(result)
# 出力結果:
#[[1.0000000e+00 0.0000000e+00]
# [8.8817842e-16 1.0000000e+00]]
先ほどとは微妙に異なる値が表示されました。これは浮動小数点数値の計算誤差によるものでしょう。「8.8817842e-16」という値にギョッとする人もいるかもしれませんが、これは指数表記なので小数点以下にゼロが10個以上並んでいることに注意してください。実質的にはゼロと同等なので、計算結果は単位行列といってもよいでしょう。とはいえ、スッキリはしません。
numpy.set_printoptions関数
浮動小数点数値などをどのように表示するかは、numpy.set_printoptions関数で設定可能です(現在の設定を読み取るにはnumpy.get_printoptions関数を使います)。
詳しいことは上記のリンクから公式のドキュメントを参照していただくとして、幾つかのパラメーターを紹介しておきます。
| パラメーター | 説明 |
|---|---|
| precision | 小数点以下の精度。デフォルトは8。floatmodeの値によって表示される小数部の精度は変化する点には注意 |
| suppress | Trueなら常に固定小数点数値として表示。Falseなら多次元配列の要素の最小値が10-4より小さいか、要素の最小値と最大値の絶対値の比率が1000倍よりも大きいときには指数表記が行われる。デフォルトはFalse |
| nanstr | NaN値の文字列表記の指定。デフォルトは「nan」 |
| infstr | 無限大を表す値の文字列表記の指定。デフォルトは「inf」 |
| sign | 浮動小数点数値の符号の表示方法。'+'なら正値でも常に符号を表示。' 'なら正値は符号の位置に空白文字を表示。'-'なら符号を省略。デフォルトは'-' |
| floatmode | precisionパラメーターの解釈方法の指定。 'fixed'なら常にprecisionで指定された桁数で小数点以下を表示 'unique'なら各値の小数部の桁数が変化する 'maxprec'ならprecisionで指定された桁数を最長の文字数として、各要素の値をその精度で表示する。ただし、より少ない桁数で表示できるものについては末尾はゼロ埋めされるのではなく空白文字が表示される 'maxprec_equal'ならprecisionで指定された桁数を最小の文字数として、各要素の値をその精度で表示する。より少ない桁数で表示できるものについては末尾がゼロ埋めされる。デフォルト値は'maxprec'(ドキュメントでは'maxprec_equal’とありますが、たぶんこちらが正解のようです) |
| numpy.set_printoptions関数のパラメーター | |
少し例を示しましょう。
x = np.array([-1.23, 2.34567])
np.set_printoptions(floatmode='fixed', precision=4)
print(x) # [-1.2300 2.3457]
np.set_printoptions(floatmode='unique', precision=4)
print(x) # [-1.23 2.34567]
np.set_printoptions(floatmode='maxprec_equal', precision=4)
print(x) # [-1.2300 2.3457]
np.set_printoptions(floatmode='maxprec', precision=4)
print(x) # [-1.23 2.3457]
上はprecisionとfloatmodeの2つのパラメーターを指定したものです(といっても、precisionは全て4としています)。このとき、最初の例('fixed')では全ての要素が指定された桁数で小数点以下の値を表示しています。次の例('unique')では、要素の値を表示するのに必要な桁数が使われています(precisionの指定は無視されます)。3つ目の例('maxprec_equal')では小数点以下の桁数はprecisionで指定された4桁となって、値の丸めが発生する一方で、全ての要素の末尾が最大の桁数に合わせてゼロ埋めされています。最後の例('maxprec')でも小数手にかの桁数はprecisionで指定された4桁となって丸めが発生している点は'maxprec_equal'とは異なり末尾がゼロ埋めではなく空白文字で埋められています。
そこでfloatmodeを'unique'にして先ほど計算したaとinvaの行列積を表示してみます。すると次のような値となっていることが分かりました。
np.set_printoptions(floatmode='unique')
print(result)
# 出力結果:
#[[1. 0. ]
# [0.0000000000000008881784197001252 0.9999999999999996 ]]
floatmodeを'unique'にしたので各値の表示桁数がバラバラになっていますが、これを見れば、単位行列との誤差はほんのわずかであることが実感できるでしょう。
さらにsuppressをTrueに指定して、precisionとfloatmodeをデフォルト値(8と'maxprec')にすれば表示は次のようになります。
np.set_printoptions(suppress=True, precision=8, floatmode='maxprec')
print(result)
# 出力結果:
#[[1. 0.]
# [0. 1.]]
これで(表示と気分が)少しスッキリしました。
行列式を求めるには
ところで、先ほどは2行2列の行列の逆行列を求める式として以下を示しました。
この式で逆行列が求められるのは、「ad−bc」が0とはならないときだけであることに気が付いたでしょうか。これが0になるような行列(の要素の組)には逆行列は存在しないということです。この値は行列に逆行列があるかどうかを示す重要な値であり、「行列式」(determinant)と呼ばれています。行列Aの行列式は、記号を使うと「|A|」とか「det(A)」などと表記されます。
なお、ad−bcはあくまでも2行2列の行列の行列式であり、各行各列の要素数が増えると行列式の計算方法も変わりますが、ここでは触れないことにします。というのは、NumPyではもちろん、行列式の計算も簡単に行えるからです。
行列式を求めるにはnumpy.linalg.det関数を使います。以下に例を示します。
a = np.array([[1, 2], [3, 4]])
deta = np.linalg.det(a)
print(deta) # -2.0000000000000004
この例では先ほどの例と同じ2行2列の行列を作成して、その行列式を求めています。この場合、「ad−bc」は「1×4−2×3」=「−2」です(浮動小数点数計算による誤差があるのはご了承ください)。
では、行列式の値が0となる行列についても考えてみましょう。
b = np.array([[4, 10], [2, 5]])
detb = np.linalg.det(b)
print(detb) # 0.0
このときにはnumpy.linalg.inv関数による逆行列の計算も例外を発生します。
result = np.linalg.inv(b) # LinAlgError
このような行列のことを「特異行列」と呼びます(一方、逆行列を持つ行列は既に述べたように「正則行列」と呼びますが、「非特異行列」と呼ぶこともあります。他に「可逆行列」と呼ぶこともあります)。
行列の固有値を求めるには
最後に行列の固有ベクトルと固有値についても簡単に紹介しておきましょう。
例えば、次のような行列があったとします。
x = np.array([[4, -1], [2, 1]])
次に以下のようなベクトルがあったとします。
v = np.array([1, 1])
この行列とベクトルの積を計算します。
result = x @ v
print(result) # [3 3]
これは元のベクトルである(1, 1)を3倍したものです。このように、行列AとベクトルvがあったときにAv = λvとなる(行列とベクトルの積が元のベクトルのスカラー倍となる)ようなλのことを行列Aの固有値、vのことを固有ベクトルと呼びます(ただし、ベクトルは零ベクトル(0, 0)であってはなりません)。
NumPyではこの固有値と固有ベクトルを計算するのにnumpy.linalg.eig関数を使います。以下に例を示します(「eig」は「own」を意味するドイツ語の「eigen」に由来しているのでしょう)。
この関数は固有値を要素とする配列と、固有ベクトルを要素とする配列の2つの配列を返すことには注意してください。また、固有ベクトルは列方向に格納されている点にも注意が必要です。
以下は上で作成した行列の固有値と固有ベクトルを得る例です。
x = np.array([[4, -1], [2, 1]])
eigvals, eigvecs = np.linalg.eig(x)
print(eigvals) # [3. 2.]
print(eigvecs)
# 出力結果:
#[[0.70710678 0.4472136 ]
# [0.70710678 0.89442719]]
この例では固有値は3と2の2つがあり、固有ベクトルも(0.70710678, 0.70710678)と(0.4472136, 0.89442719)の2つがあるということです。先ほど見た固有ベクトルは(1,1)でしたが、ここでそうなっていないのはベクトルの長さが1になるように調整をしているからです(これをベクトルの規格化といいます)。
上述したように、固有ベクトルは列に沿って並んでいることにも注意してください。固有値を要素とする配列のインデックスと、固有ベクトルの列が対応します。そのため、固有ベクトルを取り出すには「eigvecs[:, 固有値のインデックス]」のようにします(これは固有値のインデックスの値で指定される列の全ての行を得ることを意味しています)。
for idx, val in enumerate(eigvals):
print(f'{val}: {eigvecs[:, idx]}')
# 出力結果:
#3.0: [0.70710678 0.70710678]
#2.0: [0.4472136 0.89442719]
つまり、固有値3に対応する固有ベクトルは(0.70710678, 0.70710678)で、固有値2に対応する固有ベクトルは(0.4472136, 0.89442719)となります。
実際に、行列xと固有ベクトルとの積を計算して、それが固有値倍の値になっているかも確認してみましょう。
for idx, val in enumerate(eigvals):
vec = eigvecs[:, idx]
result = x @ vec
print(result)
print(result / vec)
print(val)
print()
# 出力結果:
#[2.12132034 2.12132034]
#[3. 3.]
#3.0
#
#[0.89442719 1.78885438]
#[2. 2.]
#2.0
ここでは先ほどと同様に「eigvecs[:, idx]」として、固有値に対応する固有ベクトルを得た上で、元の行列xとの積を計算しています(x @ vec)。後はその結果と、結果を固有ベクトルで除算した結果、それから固有値を出力しています。ご覧の通り、固有ベクトルが固有値倍された結果が得られました。
データ分析の世界で固有ベクトルは主成分分析や特徴量の選択などを行う場面で使うことになるでしょう(現段階ではそこまでの道のりはまだまだ先のことではありますが)。ここでは取りあえず「そんなものがあるんだな」ということを覚えておきましょう。
というわけで、今回は逆行列、行列式、行列の固有値と固有ベクトルについて紹介しました。次回は基本統計量の求め方を見ていく予定です。
Copyright© Digital Advantage Corp. All Rights Reserved.

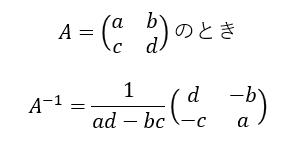
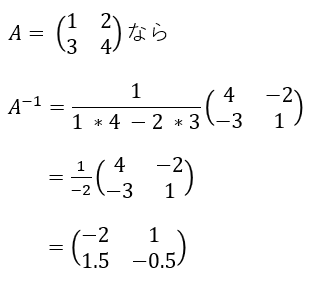 上で作成した行列の逆行列を計算
上で作成した行列の逆行列を計算




