第1回 初めてのニューラルネットワーク実装、まずは準備をしよう ― 仕組み理解×初実装(前編):TensorFlow 2+Keras(tf.keras)入門
機械学習の勉強はここから始めてみよう。ディープラーニングの基盤技術であるニューラルネットワーク(NN)を、知識ゼロの状態から概略を押さえつつ実装してみよう。まずはワークフローを概観して、データ回りの処理から始める。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本連載では、「ニューラルネットワーク」を難しくないものと捉え、できるだけ視覚的かつシンプルに説明を行う。「機械学習を始めてみたいけど、数学や統計から勉強を始めるのは大変だなぁ」と思っている人に、「まずは始めてみよう」というきっかけを与えることを目的として、記事を執筆した。
本連載の読者対象は、完全な初心者を想定している。機械学習の知識はゼロで構わず、数学は中学数学レベル(二次関数など)を見て何となく理解できるレベルで問題ない。Pythonのコードは出てくるので、不安がある場合は、下記の連載などに目を通すとよいだろう。
- 『機械学習&ディープラーニング入門(概要編)』……「ディープラーニングって何?」という人
- 『機械学習&ディープラーニング入門(コンピューター概論編)』……プログラミング未経験の人
- 『Google Colaboratory入門』……Jupyter Notebook/Google Colaboratory未経験の人
- 『機械学習&ディープラーニング入門(Python編)』……Python未経験の人
- 『機械学習&ディープラーニング入門(データ構造編)』……NumPy未経験の人
- 『Python入門』……Pythonをマスターしたい人
ニューラルネットワークは難しくない
「ディープラーニング」や、その基盤技術である「ニューラルネットワーク」について学び始めて、途中で挫折した人は少なくないだろう。実際に、ニューラルネットワークの解説を読むと、高校や大学以来、遠ざかっていた数式のオンパレードで、機械学習時の各ステップで用いられる各要素の技術/理論も多種多様である。まずこれに、面食らう人が少なくない。次に、そういった各要素を網羅的に勉強して、完全な知識としていくのは、それなりに時間のかかる大変な作業となる。このため、「本1冊最後まで読んでコードも書いてみたけど、全体的にはやっぱりよく分からない」という感想を持つ人も多いのではないだろうか。
確かに、実務で思い通りにディープラーニングを活用できるようになるまでには、やはり各要素技術/理論を十分に理解することが不可欠で、それでようやく技術や理論を適切に使い分けられるようになる。しかしながら、ニューラルネットワーク全体を概観してみると、やっていることはワンパターンで、コード内容も難しくないことに気付く。よって、とりあえずそのパターンを理解すれば、「ニューラルネットワークやディープラーニングがどのように機能するか」を理解するためのきっかけや枠組みとなるはずである。
そこで本連載では、最もシンプルなニューラルネットワークを実装しながら、そのパターンを説明する。それによって、「ニューラルネットワークがどのように機能するか」を理解することを目標としたい。
ニューラルネットワークの実装には、よりシンプルなコードとするため、Python(バージョン3.6)と、ディープラーニングのライブラリ「TensorFlow」の最新版2.0(バージョン2系)を利用する。TensorFlowには書き方が何種類かあるが、本連載では高水準APIのKeras(以下、tf.keras)を使用する。開発環境にGoogle Colaboratory(以下、Colab)を用い、ニューラルネットワークの視覚化に「ニューラルネットワーク Playground - Deep Insider」(以下、Playground)を利用する。
本連載のテーマは『仕組みの理解×初めての実装』とし、全3回で、以下のタイトルとなる。
- 前編: 初めてのニューラルネットワーク実装、まずは準備をしよう(今回)
- 中編: ニューラルネットワーク最速入門
- 後編: ディープラーニング最速入門
全3回の全てのサンプルコードは、下記のリンク先で実行もしくは参照できる。
さっそく前編の説明を始めよう!
ディープラーニングの大まかな流れ
機械学習/ディープラーニングの一般的な作業の流れは、『前掲の連載(概要編)』の「Lesson 3 機械学習&ディープラーニングの、基本的なワークフローを知ろう」という記事でも紹介しているが、本連載では、おおまかに下記の8つの工程に分けて、1ステップずつ進めることにする。
- (1)データ準備
- (2)問題種別
- (3)前処理
- (4)“手法” の選択: モデルの定義
- (5)“学習方法” の設計: モデルの生成
- (6)学習 : トレーニング
- (7)評価
- (8)テスト
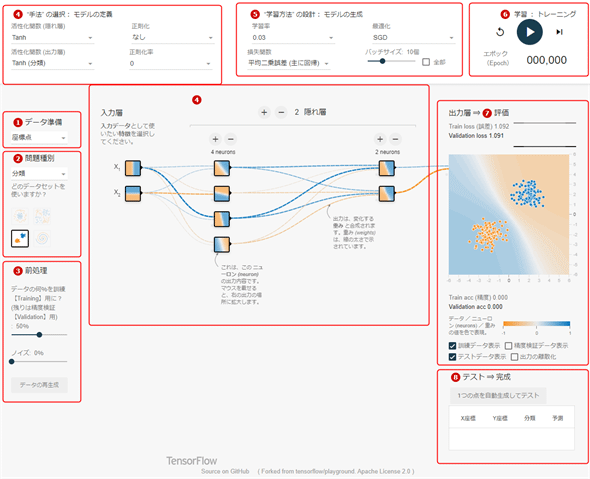
この工程は、Playground(図0-2)にある赤色の丸数字に対応している。
それでは(1)から順番に見ていこう。次回中編の(4)からニューラルネットワークの説明に入るが、その前に今回の前編ではその準備として(1)〜(3)のデータに関する説明をさせてほしい。
(1)データ準備
まず、データの準備を行う。事前に、こちらのPlayground(表示内容を絞り、初期値を設定済みのもの)をクリックして開いておいてほしい。
Playgroundによる図解
これをPlayground上で実行するには、図1-1のように、左上の(1)で「座標点」を選択すればよい(※これしか選択できない)。
ここでいう座標点とは、横のX軸が-6.0〜6.0、縦のY軸も-6.0〜6.0の数値を取る、2次元の座標系にたくさんプロット(=点描画)した全ての点のことである。今回は、このような点々データを使う。図1-2がそのプロット例である。
青色とオレンジ色の座標点がたくさんプロットされているのが分かる。点の色については後述する。
Pythonコードでの実装例
それでは、「座標点」データを準備するためのコードをPythonで記述してみよう。
点々の生成処理は、ニューラルネットワークとは関係がないので、筆者が実装したライブラリ「playground-data」を使うことにする。このライブラリをインストールするには、Colabで新規ノートブックを作って、1つのセルに以下を入力して実行してほしい(※Colabノートブックの作成方法はこちら、使い方はこちらを参照してほしい)。
!pip install playground-data
実際のデータ生成は、ステップ(3)で行う。
(2)問題種別
次に、問題種別を選択する。
Playgroundによる図解
これをPlayground上で実行するには、図2-1のように、左側の(2)で「分類(Classify)」を選択すればよい(※「回帰(Regression)」も選択できるが、今回は説明を割愛する)。
分類というのは、「写真が犬か猫か」を判定する機械学習モデルを想像すると分かりやすいだろう。今回は、「犬か猫か」ではなく、「青色(=1.0)か、オレンジ色(=-1.0)か」を判定する。
なお、前掲の図1-2で示した2次元座標系では、青色の点群は右上の方、オレンジ色の点群は左下の方に偏って存在していた。よって、点群と点群の間に「線」を引けば、線の右上にある点は青色、線の左下にある点はオレンジ色、と予測/推論できる。実際にこれを実現するのがトレーニング(=学習)後の機械学習モデル(通称:AI)なのである。
図2-2の背景色は、Playgroundでトレーニング後の機械学習モデルの予測結果を視覚化したものである(※プロットされている各点は、図1-2で示したデータと同じものである)。右上の青色の背景と、左下のオレンジ色の背景の間に白い線が出来ているのが分かるだろう。これが、前述の「線」に相当するもので、決定境界(Decision boundary)と呼ばれている。
ここまでで、「ニューラルネットワークで作成した機械学習モデルで、分類問題を解く」とは、どのようなことなのかがイメージできるようになっただろう。
なおPlaygroundでは、分類か回帰かで、選択できるデータの種類/種別が違う(※記事をコンパクトにするため、その違いの詳細は割愛する。選べる種別については後掲の図2-4を参照)。よってここで、データ種別も選択しておく。
今回は、図1-2や図2-2で示した2群に分かれて集まっている点データを使う。Playground上でこれを行うには、図2-3のように[どのようなデータセットを使いますか?]欄で「ガウシアン(Gaussian)」(=正規分布の「山」形状のように、ある基点に集中して分布するデータ)を選択すればよい。
ここでは「ガウシアン」を選択したが、それ以外のデータセットの表示例を参考までに図2-4にまとめた。
![図2-4 [どのようなデータセットを使いますか?]で選択できるデータセットの表示例](https://image.itmedia.co.jp/ait/articles/1909/19/di-02-4.gif) 図2-4 [どのようなデータセットを使いますか?]で選択できるデータセットの表示例
図2-4 [どのようなデータセットを使いますか?]で選択できるデータセットの表示例分類(=例えば犬猫のような離散的なデータの予測。この例では「青色か、オレンジ色か」)の場合は、円/XOR/ガウシアン/螺旋(らせん)が選択可能。
回帰(=例えば気温のような連続的なデータの予測。この例では「青色〜オレンジ色と連続する範囲のどのあたりの値か」)の場合は、平面/マルチガウシアンが選択可能。
Pythonコードでの実装例
それでは、「分類問題」と「データ種別」を設定するためのコードをPythonで記述してみよう。
なお本連載では、Pythonのバージョン3系を必須とする(※Colabにインストール済みのPythonバージョンが分からない場合は、import sys; print('Python', sys.version)を実行すれば、バージョンを確認できる)。Pythonのバージョンは、Colabにデフォルトでインストール済みのものをそのまま使えばよいはずだ(※2019年9月17日の執筆時はPython 3.6.8だった。バージョンの切り替え方法はこちらを参考にしてほしい)。
ここでは、ライブラリ「playground-data」のメインパッケージであるplygdataをpgという別名でインポートし、その中で定義されているDatasetTypeクラスのClassifyTwoGaussDataクラス変数の値(=分類で、2つのガウシアンデータ)を、定数PROBLEM_DATA_TYPEに代入することで(リスト2)、これを表現する。この定数をpg.generate_data()関数に指定して実際のデータ生成を行うが、このコードは後述のリスト3で説明する。※なお、データ生成方法は本連載独自のコードであるため、コード内容が理解できるよう意味を説明しているが、内容を覚える必要はない。
# playground-dataライブラリのplygdataパッケージを「pg」という別名でインポート
import plygdata as pg
# 問題種別で「分類(Classification)」を選択し、
# データ種別で「2つのガウシアンデータ(TwoGaussData)」を選択する場合の、
# 設定値を定数として定義
PROBLEM_DATA_TYPE = pg.DatasetType.ClassifyTwoGaussData
# ※実際のデータ生成は、後述の「pg.generate_data()関数の呼び出し」で行う
(3)前処理
それでは、実際のデータ生成を行おう。通常の機械学習では、収集しておいたデータから、使うデータを選別し、さらに機械学習モデルへの入力データとして使えるように欠損値を埋めたりなどして整え、最終的に、
- 学習用のデータ(=トレーニングデータ。以下、「訓練用」「訓練データ」と表記)
- 評価用のデータ(=精度検証データ。以下、「精度検証用」「精度検証データ」と表記)
に分割する。今回は独自にデータ生成を行うので、通常とは違い、これらの作業はひとまとめに行えるようになっている。
Playgroundによる図解
実際にPlayground上で行っているのが、図3-1だ。
図3-1のように、Playgroundの左側の(3)で[データの何%を訓練【Training】用に?]は「50%」を指定し、[ノイズ]は「0%」を指定する。
訓練用/精度検証用のデータ分割について
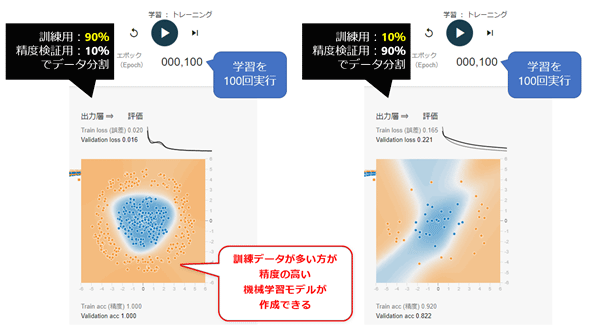
説明するまでもないと思うが、例えば訓練用を80%と指定すると、残りの20%が精度検証用になる。当然ながら、訓練データが多いほど、精度が高くなる。図3-2は、訓練データを最大の90%にした場合(左)と最小の10%にした場合(右)に、どちらも100回(学習単位は「エポック」と呼ばれる)学習した結果(背景)の比較である(※なお、この比較例では、差異が分かりやすくなるよう、データ種別として、より複雑な「円(サークル)」を選択した上で学習を実行した)。
左の90%の背景が色濃くきれいな円になっており、高い精度のモデルが生成できたことが分かる。
だからといって訓練データを何が何でも多くすればよいわけでもない。精度検証データが少なすぎると、「十分な評価ができない」という問題も生じる。適切な割合は、「機械学習&ディープラーニング入門(概要編) Lesson 3」を参考にしながら、自分で考えて決める必要がある。今回は、データを半々に分けている。
ノイズについて
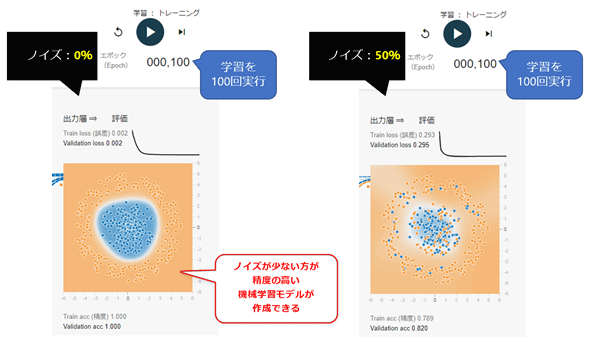
前掲の図3-1にあった[ノイズ]についても説明しておこう。ノイズ(noise)とは「外れ値などの余計なデータ」のことで、今回の座標点データセットでは、ノイズの数値を大きくすると、点群の散らばりが広くなる。当然ながら、ノイズが少ないほど、精度は高くなる。図3-3は、ノイズを最小の0%にした場合(左)と最大の50%にした場合(右)の、訓練データのプロット例(点描画)と、学習結果の比較(背景)である
左の0%の方は背景が色濃くきれいな円になっており、高い精度のモデルが生成できたことが分かる。
このように基本的には、ノイズや外れ値は取り除いた方が、学習の収束が早く、モデルの汎化性能(=未知のテストデータに対する学習済みモデルのパフォーマンス)も高まる。一方で、画像認識では画像にわざとノイズを乗せてより多く学習することで、より安定した学習モデルに仕上げるというテクニックがあるのも知っておいてほしい。要は、ノイズもケースバイケースで考えながら処理する必要があるというわけだ。今回は、ノイズを0%にしている。
Pythonコードでの実装例
それでは、「訓練用/精度検証用へのデータ分割」と「ノイズ」を指定してデータ生成するためのコードをPythonで記述してみよう。これは次のようなコードになる。
# 各種設定を定数として定義
TRAINING_DATA_RATIO = 0.5 # データの何%を訓練【Training】用に? (残りは精度検証【Validation】用) : 50%
DATA_NOISE = 0.0 # ノイズ: 0%
# 定義済みの定数を引数に指定して、データを生成する
data_list = pg.generate_data(PROBLEM_DATA_TYPE, DATA_NOISE)
# データを「訓練用」と「精度検証用」を指定の比率で分割し、さらにそれぞれを「データ(X)」と「教師ラベル(y)」に分ける
X_train, y_train, X_valid, y_valid = pg.split_data(data_list, training_size=TRAINING_DATA_RATIO)
リスト3ではまず、データ分割の割合を指定するTRAINING_DATA_RATIOと、ノイズを指定するDATA_NOISEという2つの定数を定義している。
その次に、pg.generate_data()関数を呼び出してデータを生成し、変数data_listに代入している。関数の引数には、リスト2で定義した定数PROBLEM_DATA_TYPEで「問題種別(分類)+データ種別(2つのガウシアンデータ)」を、さらに定数DATA_NOISEで「ノイズ(0%)」を指定している。
生成されたdata_list(多次元リスト値)と、定数TRAINING_DATA_RATIOで「ノイズ(訓練用を50%)」を引数に指定して、pg.split_data関数を呼び出してデータを分割している(ちなみに、このsplit_data関数は、データ分割でよく使われるライブラリ「scikit-learn」のtrain_test_split関数を模して作ったものだ)。分割後のデータは以下の変数に代入されている。
- X_train: 訓練データの座標点(X)。N行2列のデータ
- y_train: 訓練データの教師ラベル(y)。N行1列のデータ
- X_valid: 精度検証データの座標点(X)。N行2列のデータ
- y_valid: 精度検証データの教師ラベル(y)。N行1列のデータ
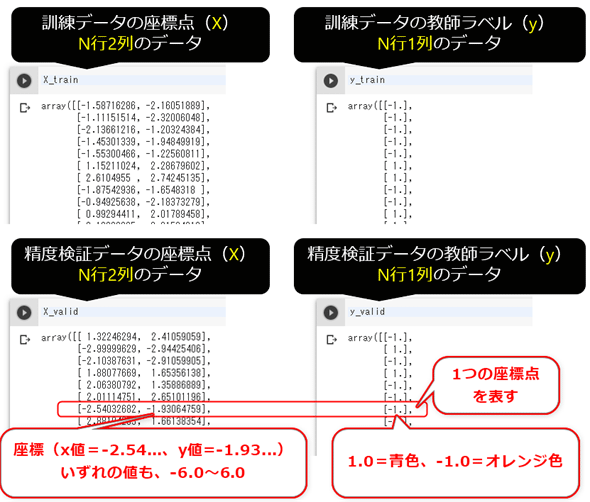
いずれの変数も、ライブラリ「NumPy」の多次元配列値となっている(※ディープラーニングのライブラリは基本的にNumPyに対応しているのでそのまま使用できる)。具体的にどのようなデータが入っているかというと、図3-4がその一部の出力例である。
各行は、個々の座標点を表している。
座標点(X)にある2列の数値の意味は「座標(横のX軸上の値、縦のY軸上の値)の点」であり、前述の通り、いずれも基本的に-6.0〜6.0の数値を取る。
教師ラベル(y)にある1列の数値の意味は、前述の通り、1.0=青色、-1.0=オレンジ色である。
以上でデータの生成(通常はデータの取得〜前処理)は完了だ。あとは上記の各データ変数を使って、ニューラルネットワークを説明していく。
今回前編ではワークフローの全8工程のうち、(1)〜(3)のデータに関する処理内容を説明した。今回のデータを、次回中編の(4)から説明するニューラルネットワークで使っていくことになる。次回は、ニューラルネットワークの基本単位であるニューロンの説明から始める。前編・中編・後編の三部作は、まとめて読むことで価値があるので、ぜひ次回中編も継続して読み進めてほしい。Please follow on Twitter @DeepInsiderJP.
Copyright© Digital Advantage Corp. All Rights Reserved.

 図0-1 あい博士「ニューラルネットワークは難しくない!」、マナブくん「えー……」
図0-1 あい博士「ニューラルネットワークは難しくない!」、マナブくん「えー……」

![図1-1 [データ準備]で「座標点」を選択](https://image.itmedia.co.jp/ait/articles/1909/19/di-01-1.gif) 図1-1 [データ準備]で「座標点」を選択
図1-1 [データ準備]で「座標点」を選択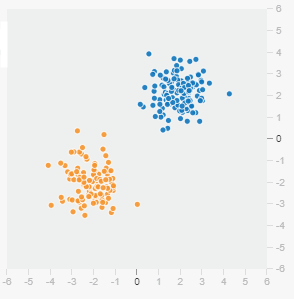 図1-2 座標点がプロットされた2次元座標系
図1-2 座標点がプロットされた2次元座標系![図2-1 [問題種別]で「分類」を選択](https://image.itmedia.co.jp/ait/articles/1909/19/di-02-1.gif) 図2-1 [問題種別]で「分類」を選択
図2-1 [問題種別]で「分類」を選択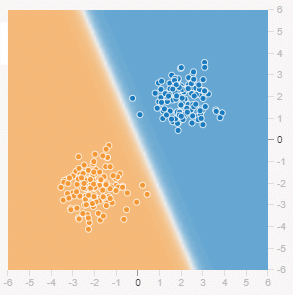 図2-2 訓練後の2次元座標系(白い部分が境界線)
図2-2 訓練後の2次元座標系(白い部分が境界線)![図2-3 [どのようなデータセットを使いますか?]で「ガウシアン(Gaussian)」を選択](https://image.itmedia.co.jp/ait/articles/1909/19/di-02-3.gif) 図2-3 [どのようなデータセットを使いますか?]で「ガウシアン(Gaussian)」を選択
図2-3 [どのようなデータセットを使いますか?]で「ガウシアン(Gaussian)」を選択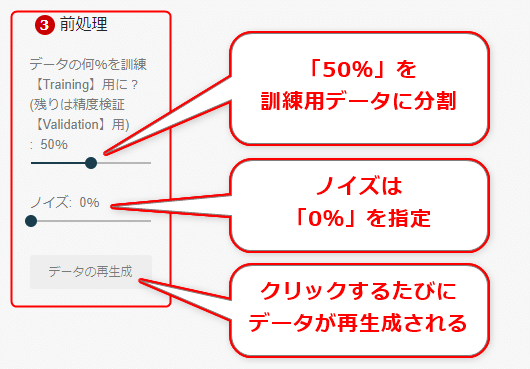 図3-1 前処理として訓練用/精度検証用へのデータ分割やノイズを設定
図3-1 前処理として訓練用/精度検証用へのデータ分割やノイズを設定