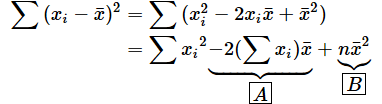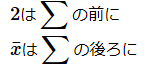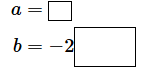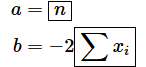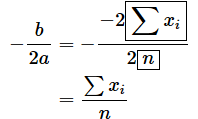[AI・機械学習の数学]総和を表すΣは機械学習に必須の記号:AI・機械学習の数学入門(4/5 ページ)
応用:Σを使って平均値を求める式を導き出す
前回、具体的な数値を使って、各データとの距離の二乗和が最小になるときの
の値こそが平均値である、というお話をしました。また平均値の話か、と思われた方もおられるかもしれませんが、前ページで示した目標【その2】の公式を使ったΣの計算に慣れるのに恰好(かっこう)のネタなので、少しお付き合いください。また、新たな気づきも得られるはずです。
さて、今回は、数値の代わりに文字を使い、総和をΣで表してみます。そうすれば、平均値を求める式を一般的に表すことができそうですね。そこで、各データを{x1,x2, ... , xn}とし、各データとの距離の二乗和が最小になるときの値を
として、
を求める式を導き出してみましょう。
図で表すと、以下の
が
を求めるということです(図3)。なお、2乗の総和のことを「二乗和(じじょうわ)」と略して呼びます。ここからは動画でも分かりやすく解説しているので、難しく感じた人は次の動画2を視聴してみてください。
動画2 距離の二乗和を最小にする「xバー」を求める(総和Σ活用編)
では、前回と同じようにやってみましょう。まず、
します(=距離の2乗を求める)。そして、それらを全て足します(=総和を求める)。
です。ここで、Σを使ってこの式を書いてみてください。またまた穴埋めです。「どこから」「どこまで」は自明なので省略しちゃいましょう。
答えは以下の通りです。
要するに、Σの中の式では、x1,x2,...,xnを一般的にxiと表せばいい、ということですね。
続いて、Σの中の式を展開していきましょう。展開? え? 何言ってるか分からない、という人もいるかもしれませんが、これまでに学んだ知識を思い出してください。
の部分を見てみると、(a−b)2=a2−2ab+b2の公式の左辺と同じ形になっていることに気がつきます。
です。従って、以下のように展開できます。
次に、目標【その2】で見たΣ(xi + yi) = Σxi + Σyiという公式を使ってみます。
[A]の項を見てください。
には添字が付いていないので定数として扱えます。
書かれていますが、単なる掛け算です。これは、
という公式を使っただけです。
[B]の項は単に
だけなので、
となりますね。
てみると、以下のようになります。
これが、
ですね。よくよく見ると、これは
です。ということは前回と同じように、平方完成すれば、
が求められます。が、わざわざ計算しなくても、係数だけを見れば
が求められることが分かっていました。つまり、
という式でaが正であれば、
を求めるだけでいい、というわけです(※この内容が分からない場合は、前回の平方完成の説明をもう一度確認してみてください)。そこで、式を見比べてみましょう。枠内には(2)式の係数を当てはめてみてください。
答えは、
ですね。従って、
となります。これで、(2)式全体を最小にする値が
だということが分かりました。ところで、
って何でしょう。Σは全ての値を足すこと、nは値の個数なので、日本語で言うと「全ての値を足して個数で割ったもの」となります。これは平均値を求めるための式そのものです!
ということで、各データとの距離の2乗の総和(二乗和)を最小にする値は、全ての値を足して個数で割れば求められること、そして、それが平均値(算術平均)である、ということが一般的に表せた、というわけです。
ここでは、Σの公式に慣れるために上のような計算をしてみましたが、実はそれ以上の意味合いがあります。それは、このような式の変形は、たくさんの項を+でつないで総和を求める書き方だと簡単には表せないということです。Σという記号を使ったからこそ、このような計算ができたのだ、ということが重要です。
数学で、さまざまな記号を使うのには、複雑な計算が簡単に表せるというメリットがあるからです。繰り返しになりますが、謎の呪文を使ってイジワルをしようというわけではないのです。
応用:重心を求める
最後に、次のページで「重心を求める」について解説します。これまでに学んだ知識を総動員しましょう。復習も兼ねています。
Copyright© Digital Advantage Corp. All Rights Reserved.

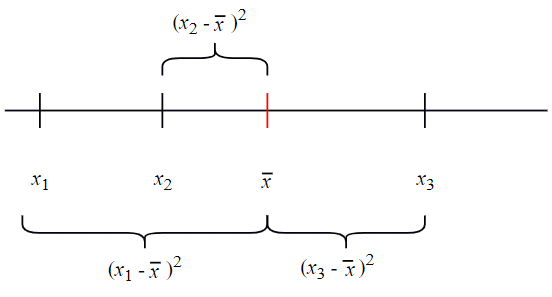 図3 各データからの距離の二乗和が最も小さくなる点を求める
図3 各データからの距離の二乗和が最も小さくなる点を求める