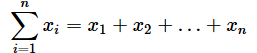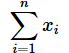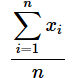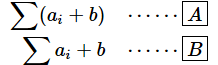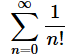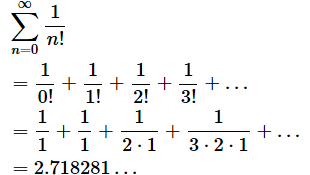[AI・機械学習の数学]総和を表すΣは機械学習に必須の記号:AI・機械学習の数学入門(1/5 ページ)
「Σ」を理解して総和をマスターしよう。応用で、Σの公式を使って平均を求めてみる(最小二乗法につながる基礎知識)。さらに、平均を使って重心を求める計算も行う(クラスタリング「k-means法」につながる基礎知識)。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回までで、中学までの数学のうち、最低限の知識についておさらいしました。演算のルールと文字式の取り扱いだけでしたが、それでも機械学習で使われる数学を垣間見ることができたと思います。添字は中学の数学には登場しなかったかもしれませんが、文字式の延長で理解できますね。
今回は、多くの数を足すときに便利な「総和」の記号Σの使い方を見ていきます。Σが使いこなせるようになると、複雑な計算も簡単に表せるようになります。
目標【その1】: 総和を求める
今回の最初の目標は、「総和」を求めるために使うΣの意味と書き方を理解することです。例えば、以下のような式に見覚えがあるでしょう(高校2年ぐらいの数学です)。
Σは「総和を求める」つまり「全部足す」ということを表す記号で「シグマ」と読みます。機械学習のための計算でよく登場するので、書き方と意味を丁寧に見ていきましょう。
解説:Σの意味と書き方をマスターする
前回、平均値を求める計算のお話をしました。平均値を求めるには「全ての値を足して、個数で割る」という計算をしますが、その「全ての値を足す」という部分を前回までの知識で書くと、以下のようになります。
上の式では、データの個数はn個ということになります。合計を求めるだけならこの書き方だけで十分な気がしますが、+や...という記号を幾つも書くのは面倒です。そこで、「こういうお約束に従って、全部足すんだよ」ということを簡単に表すための記号を使うことにしましょう。
それがΣです。この記号はギリシア文字のアルファベットのシグマ(大文字)で、英語で言えば、合計(SUM)の頭文字であるSに当たる文字です。Σの筆順は以下の通りです。
(1)式をもう一度見てください。xiという書き方を使って各データを表すのであれば、iの値を1,2,...nと変えて全て足すことにすればいいでしょう。このとき「全て足す」「iの値は1から始める」「iの値はnまで」「xiを」といちいち言うのが面倒なので、Σという記号を使って図2のように表します。
書き方を確認しておきましょう。Σの下には「どこからか」を、上に「どこまでか」を書き、右に「何を足すのか」を書きます。上の式の意味を改めて日本語で書き下すと「iが1から」「nまで」「xiを足す」ということになります。人によって読み方が違うかもしれませんが、この式は「シグマ、アイ、イコール、いちから、エヌまで、エックスアイ(をたす)」のように読みます。()内に書いたように、「シグマ」と意味は重なりますが、最後に「をたす」と付けることもあります。従って、
です。Σという記号はちょっとイカツイ面構えをしていますが、左辺を見ると、式を書く手間もスペースも省けることが分かります。しかも、足し算で表していたときの、途中の「...」が要らなくなったので、あいまいさがなくなり、どのような計算をするのかが正確に表せるようになりました。
なお、文章の中で数式を書く場合は、下限と上限を右下と右上に書いて、
のように表すこともあります。せっかくなので、ちょっと読んでみてください。答えは、オレンジ色の部分をクリックまたはタップすると表示されます。
は シグマ 、 アイ 、イコール、 いち から、 エヌ まで、 エックスアイ (をたす)と読みます
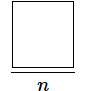
また、データが幾つかあって、それらを全部足すといった場合など、「どこからか」「どこまでか」が文脈から明らかな場合は、下限と上限を省略して、以下のように書くことがあります。
では、ちょっとしたクイズです。x1からxnまでの平均値を求める式を、Σを使って書いてみてください。ここでは、「どこから」「どこまで」を省略せずに書いてみまょう。
答えは以下の通り。真ん中にΣを書いて、下に添字の下限、上に上限、右に足し算をする値(文字)を書くだけです。既に見た通りでしたね。
Σとは要するに足し算です。何番から何番まで何を足す、と言う代わりに記号を使って簡潔に表しているだけのことです。別に謎の呪文を使ってイジワルをしようというわけではなく、カンタンに表したいだけのことなのです。
ここで、Σに関する言い回しで重要な補足をしておきます。これまで、書き方の説明として「Σの右にxiを書く」といった言い方をしてきましたが、意味としては、このxiはΣを使って合計する範囲の中にあるものなので、今後は「Σの中のxi」のような表し方にします。以下の例で確認しておいてください。
[A] …… Σの中の式は(ai+b)
[B] …… Σの中の式はaiだけ。bはΣの外
今回はもう少しお話がありますが、Σの書き方と意味が一通り分かったので、いったん練習問題に取り組んでみましょう。
練習問題
解答例
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

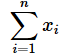
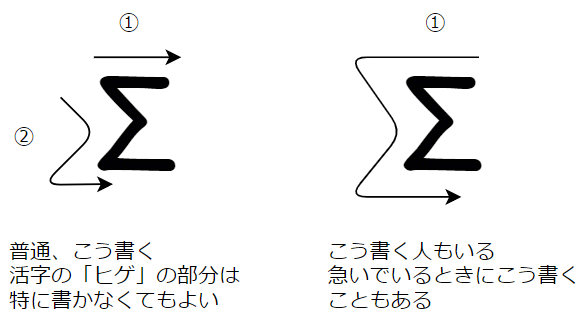 図1 Σの筆順
図1 Σの筆順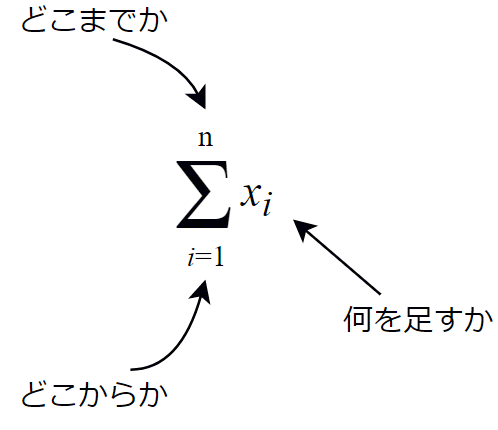 図2 Σの書き方と意味
図2 Σの書き方と意味