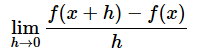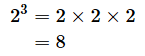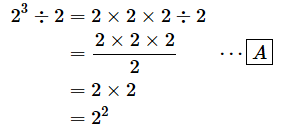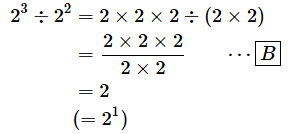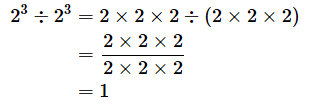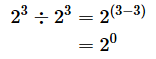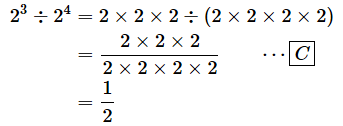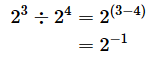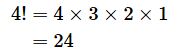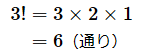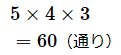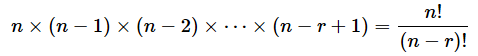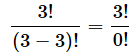[AI・機械学習の数学]「0」の取り扱い:AI・機械学習の数学入門
連載の通常の流れとは別の番外編。「0」の取り扱いについて3つのポイントを解説。0で割ること、0乗、0の階乗について説明する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
今回は連載の通常の流れとは別枠の「番外編その1」です。コラムを読むような気持ちで気楽に読んでみてください。通常とは異なり、例題や練習問題はありません。ポイント解説のみの短い記事です。
数学史では0の発見などについての興味深いさまざまな話がありますが、ここでは、そういった話ではなく、実用面に絞って0の取り扱い方を整理しておきます。今回は中学/高校数学の基礎のおさらいとなっており、基本的な約束事からべき乗や階乗での0の取り扱いについて見ていきます。
ポイント1 「0」で割ってはいけない
0で割り算(0除算)することはできない、というのはもはや常識といってもいいでしょう。一方、0を何かで割ることはできます。その場合の答えは0です。
プログラミング言語では、多くの場合、リスト1.1のように0で割り算をするとエラーになります(中には「無限大(∞)」と表示されたりするものもあります)。
>>> a=10
>>> b=0
>>> print(a/b)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ZeroDivisionError: division by zero …… エラーが表示された
>>>
具体的な数字を使っている場合には間違えることはないと思いますが、文字式では、割る数(つまり分母)が0になっていないことを確認しておく必要があります。また、プログラミングでは0での割り算が起こったときに備えての対応が必要です。なお、「0に限りなく近づく」という場合は0ではありません。以下の式は導関数の定義でしたね。この場合、hの値は限りなく0に近づきますが0ではありません。
ポイント2 何かを0乗すると1になる
どのような値であっても0乗すると1になる、というのを一般的に表すと以下のようになります。
このことを具体的な値で確かめておきましょう。べき乗というのは、同じ数を何回か掛けることでしたね。例えば、2の3乗は2を3回掛けることを表します。
答えは8です。では、2の3乗を2で割るとどうなるでしょうか。
[A] …… 2で約分できる
2の3乗を2で割ると、2の2乗になりますね。答えは4です。このことから、同じ値で割り算をするなら、指数を1つ減らせばいいということが分かります。では、2の3乗を2の2乗で割ってみるとどうなるでしょうか。
[B] …… 2×2で約分できる
2の3乗を2の2乗で割ると、答えは2になります。これは2の1乗です。やはり、以下のように指数を2減らせばいいということですね。
では、2の3乗を2の3乗で割ってみましょう。ある数を同じ数で割っているので、答えは1になるはず。これまでと同じように、掛け算と割り算でも表してみます。
これを、指数を加減した式で表すと、以下のようになります。
というわけで、20=1ということが分かりました。このことは、どんな値についても言えることなので、一般的に表すと最初に示したような以下の式になります。
さらに、2の3乗を2の4乗で割ってみましょう。
[C] …… 2×2×2で約分できる
指数を加減した式で表すと、以下のようになります。
つまり、
となります。これも一般的に表すと以下のようになります。
0を通り過ぎて、マイナスの話になってしまいましたが、指数を減らして「0乗」になる場面は、微分や偏微分でも登場しましたね。
ポイント3 「0」の階乗は1
階乗とは、値を1つずつ減らしていきながら1まで掛けるという計算で、値の後に「!」を付けて表します。例えば、4の階乗であれば、以下のようになります。
0の階乗、つまり0!の答えはいくらになるでしょうか。直感的には0のような気がしますが、実はこの答えは1です。
これは「そう取り決めておくと都合がいい」からです。
せっかくなので、階乗についても簡単に復習しておきましょう。階乗は順列や組み合わせの計算、確率の計算でよく使われます。例えば、A、B、Cの3人を順に並べる方法が何通りあるかを求めるには、最初の人が3人のうちのいずれかなので3通り、そのそれぞれに対して、次が2人のうちのいずれかなので2通り、最後は1人なので1通りです。従って、
となるわけです。また、A、B、C、D、Eの5人から3人を選んで順に並べるなら、以下のようになります。
階乗を使ってこれを表すなら、以下のようにできますね。
一般に、n個のうちからr個を選んで順に並べる場合の数(順列)は、以下の式で表されます。
A、B、C、D、Eの5人から3人を選んで順に並べる場合なら、nが5、rが3になります。上の式にそれらの値を当てはめてみると納得できるはずです。ところで、n=rの場合はどうなるでしょう。つまりn人の中からn人を選んで並べる場合です。
例えば、最初の例は3人のうちから3人を順に並べることになるので、それに当てはまりますね。上の式(の右辺)でn=3、r=3とすると、以下のようになります。
答えは最初に計算した通り、3!でした。ということは、0!=1としないとつじつまが合わないですね。そういった理由もあって、0!=1と定義されている、ということです。
今回の番外編は0の取り扱いについての留意点を見ましたが、折に触れて「=」の取り扱いや「自然対数の底e」のお話など、横断的なテーマを取り上げることとします。
Copyright© Digital Advantage Corp. All Rights Reserved.