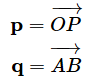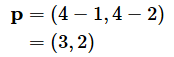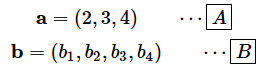[AI・機械学習の数学]ベクトルの基本と類似度の計算:AI・機械学習の数学入門(1/4 ページ)
機械学習では、普通、多くの変数や係数を同時に取り扱う。そのような場合にそれぞれの変数や係数を別々に取り扱うと数式が煩雑になってしまう。ベクトルや行列を利用すれば、複数の値をひとまとめにして取り扱えるので、数式が極めて簡潔になる。今回はベクトルについて、基本的な計算方法を紹介する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
第4回〜第8回までは微分について説明しました。機械学習の数学において微分は特に重要です。もう一つ重要なのが線形代数です。今回からは線形代数について学んでいきます。まずはベクトルの基本を学びましょう。
ベクトルについては、「大きさと向きを持った矢印のようなもの」というイメージを持っている人も多いと思います。高校の数学でもそういった例から話が始まっているはずです。もちろん、それは間違いではありませんが「位置」と「角度」を表す方法としてベクトルを使う、と言った方が応用の幅が広がります。また、ベクトルというものがあって何らかの(面倒な)ルールで計算する、と考えるよりも、複数の値をひとまとめにしてベクトルとして取り扱うと、複雑な計算が簡単にできるようになる、と考えた方が腑(ふ)に落ちることが多いと思います。
まずは、ベクトルの基本についておさらいしておきましょう。
目標【その1】: ベクトルとは
ベクトルとは、大きさと方向を合わせた量のことで、例えば点Oから点Pへの距離と方向、つまりベクトルOPを以下のように表します。
このように書くのはけっこう面倒なので、以下のように文字を太字で書いてベクトルを表すこともあります。この連載でも基本的に以下の書き方を使います。
例えば、点Oの座標が(0,0)、点Pの座標が(3,2)であれば、以下のように座標を使った表記もできます。この表し方を成分表示と呼びます。この例なら3と2が成分です。
成分表示のかっこには以下のように[]を使うこともあります。また、成分を縦に書くこともあります。
なお、基準となる点から見たある点の位置をベクトルで表したものを位置ベクトルと呼びます。取りあえず、位置ベクトルは点の座標を表すもの、と考えても差し支えありません。また、ベクトルを、単に複数の値をひとまとめにしたものと考えても構いません。
ベクトルに対して、通常の数値のことをスカラーと呼びます。
解説【その1】: ベクトルとは
目標で述べた内容については、高校数学のベクトルで最初に取り扱う内容なので、ほとんどの人にとっては既に知っている話かもしれません。念のため、図を使って解説しますが、先を急ぐ方は「ベクトルの定数倍と和の計算」や「ベクトルの内積を求める」に進んでいただいても構いません。
ベクトルの図形的なイメージを確認しておくと以下のようになります。
ここには、
という2つのベクトルが描かれていますが、以下のように1文字で表した方が簡単ですね。
ここで、ベクトルpとベクトルqは平行移動するとぴったりと重なるので、等しいものとみなされます。
成分表示にすると、
というのは簡単に分かりますが、qはどう表せばいいのでしょうか。等しいわけですから、成分表示も同じにならないといけないですね。というわけで、終点Bの座標(4,4)から始点Aの座標(1,2)を引いてX方向の大きさとY方向の大きさを求めます*1。
*1 pの方は、たまたま始点が(0,0)だったので、終点の座標がそのまま成分表示になりましたが、やはり、上と同じように終点の座標から始点の座標を引いて求めたわけですね。
成分は「距離」ではないので負になることもあります。例えば、
なら、(1-4,2-4)つまり(-3,-2)となります。なお、逆向きのベクトルは「−」を付けて表すことができます。例えば、
であれば、
と表されます。成分表示にすると、各成分の符号を逆にすればいいということも分かりますね。
ここでは、平面の例でベクトルの表し方を見ましたが、次元が増えても考え方は同じです。また、成分表示の場合、具体的な数値ではなく文字が使われることももちろんあります。いくつか例を示しておきましょう。
(例)
[A] …… 三次元ベクトル(X座標が2、Y座標が3、Z座標が4と考えればよい)
[B] …… 四次元ベクトル(図形的に表せないが、それぞれの軸の成分がb1、b2、b3、b4のベクトル)
四次元以上になると図で表すことはできませんが、多次元の空間の中で大きさと方向を持った値と考えることができます。ただ、あまり図形に頼って考えるよりは「そういうルールに従って取り扱えるもの」と割り切って捉えた方がかえって受け入れやすいのではないかと思います。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


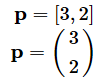
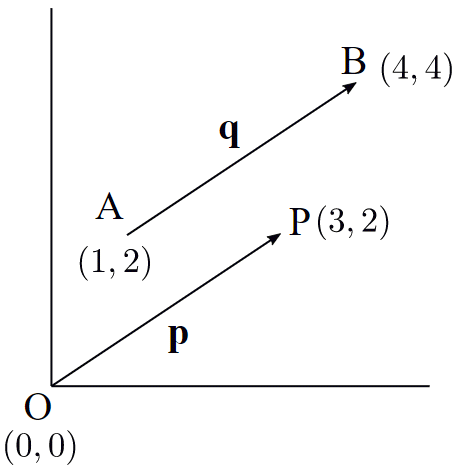 図1 ベクトルのイメージ
図1 ベクトルのイメージ