［評価指標］適合率（Precision、精度）とは？：AI・機械学習の用語辞典

用語「適合率」について説明。二値分類タスク（問題）に対する評価指標の一つで、機械学習モデルによる予測値が「陽性」で、かつ、実際の正解値も「陽性」だった正解数（＝TP）を、「陽性」と予測した全てのデータ数（＝TP＋FP）で割った値を指す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

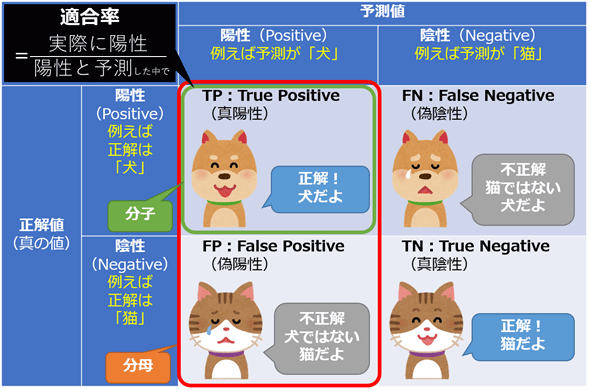
　統計学／機械学習における適合率（Precision、精密さ、精密度、精度）とは、（基本的に）二値分類のタスク（問題）に対する評価指標の一つで、「陽性（Positive、正例）」と予測したデータの中で実際に「陽性」が正解だった確率である。0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどより良い。

　言い換えると適合率は、機械学習モデルによる予測が陽性だった場合に、どれくらい正解に「適合」できるか、を表現したものだ。適合率の計算は、予測値が「陽性」で、かつ、実際の正解値も「陽性」だった正解数（＝TP）を、「陽性」と予測した全てのデータ数（＝TP＋FP）で割ることで計算できる（図1）。

図1　「適合率」のイメージ

　二値分類の混同行列を使ってあらためて計算式を書き出すと以下のようになる。

　適合率は、「陽性」の予測がより正確になっていることが重要な場面で使いやすい評価指標である。例えばあなたが果物屋さんで「個々のお客さんに対し、りんごの購入が必要かどうか」という二値分類を予測する機械学習モデルを作成したとする。

　このケースでは、「購入が必要」という陽性予測は、より正確で（＝「FP：偽陽性」ができるだけ低く）なければならないだろう。もし間違ってしまうと、リンゴを買ってもらう機会を損失してしまうからだ。

　一方で、「購入が不要」という陰性予測が、不正解であっても（＝「FN：偽陰性」が高くても）それほど問題ではない。なぜなら、実際にはリンゴの購入が不要である人に間違ってリンゴの購入をお勧めしてしまったとしても、いずれにしろ買ってはもらえず、結果的にはお店のメリットにはならないからだ。つまり果物屋さんにとっては、売れない予測についてはハズレようと実利面からは無視しても構わず、売れる予測の精密度を強化する方がより重要ということである。

　このケースでの評価指標としては、正解率（accuracy）や再現率（Recall、「FN：偽陰性」の低さを重視した評価指標）よりも適合率（「FP：偽陽性」の低さを重視した評価指標）を採用する方が好ましいと考えられる。まとめると適合率は、「陽性予測においては、できるだけ不正解を出したくない場合」に使えばよい。

　なお適合率は、場合によっては「精度」と記載される場合があるので注意が必要だ。「精度」という用語は一般的な意味で使われることが多く、その場合、「精密度（precision）」という意味ではなく「性能（performance）」もしくは「正解率（accuracy）」という意味である。混乱を避けるためにも、「精度」ではなく「適合率」や「precision」と表記したり説明したりする方が無難だろう。

　本稿で説明した「陽性予測に対する適合率」は陽性適中率とも呼ばれる。また「陰性予測に対する適合率」、つまり「陰性（Negative、負例）」と予測したデータの中で実際に「陰性」が正解だった確率は陰性適中率とも呼ばれる。

「AI・機械学習の用語辞典」