PyTorchでCIFAR-10を基にDCGANで画像生成をしてみよう:作って試そう! ディープラーニング工作室(1/2 ページ)
前回に作成したDCGANと同様な構造のニューラルネットワークモデルで学習をしながら、識別器が算出する値と損失関数の関係などについて考えてみましょう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
今回の目的
前回は畳み込みニューラルネットワークを使用したGAN、いわゆるDCGANを作り、MNISTの手書き数字っぽい画像を自動生成してみました。今回は、その学習時にフォーカスを当てて、実際にはどんなふうに学習が進んでいるのかを見てみることにしました。
といっても今回行ってみるのは、前回に紹介したDCGANの論文や、難しい数式をベースに話をするのではなく、識別器(ディスクリミネーター)からの出力がどんな値になっているかを主な話題とするつもりです。
そこで、識別器と生成器の役割について、ここで一度振り返っておきましょう。
- 識別器:訓練データおよび生成器から得た偽データを入力して、それらがどちらのデータであるかを識別する
- 生成器:識別器をうまいことだませるようなデータを生成する
DCGAN(Deep Convolutional Generative Adversarial Network)の「Adversarial」は「敵対的」という意味でした。このことからも分かる通り、識別器と生成器は相反する目的を持っています。識別器が訓練データと偽データとを完璧に識別できるのであれば、生成器が出力するデータの品質はあまり高くないと考えられます。DCGANは画像生成を目的する以上、これでは意味がありません。かといって、生成器が出力するデータがどんなものであっても、識別器が簡単にだまされるようでは、やはり問題です。
両者がいい感じに学習を進めて、最終的には生成器からの出力が訓練データと同等なものとなるのがベストです。そうなったときには、識別器は生成器からのデータを時には訓練データと識別し、またある時にはそれを偽データとして識別するようになるのではないでしょうか。と同時に、訓練データについても同様に訓練データと正しく認識することもあれば、偽データと間違って識別するようにもなるでしょう(識別器は最終的に負ける立場にあると考えられます)。
ここで、識別器をD()、生成器をG()、訓練データをx、生成器から得た偽データをG(z)とします(zは潜在変数で、前回までに見てきたようにここでは100次元の乱数です)。そうすると、識別器に訓練データを入力して得られた推測値はD(x)、識別器に生成器から得たデータを入力して得られた推測値はD(G(z))と表せます。これらを使って上の条件を表現してみましょう。
識別器の目標とするところは、学習が十分に進んだらD(x)が1(訓練データが入力された)という結果を返すように、D(G(z))は0(偽データが入力された)という結果を返すようになることです。一方、生成器が目標とするところは、D(G(z))が1(訓練データが入力された)という結果を返すような画像を生成することです。
前回作成したものと同様なニューラルネットワークモデルが果たして、そのような結果をもたらすかを、識別器の出力(や損失関数のグラフ)を見ながら考えてみるのが、今回の目的です。
コードについて
今回はMNISTではなく、CIFAR-10を使って画像を生成することにしました。ただし、識別器と生成器の基本構造は前回と変わりません(これらのコードはその都度、示すことにしましょう)。
また、CIFAR-10を読み込むことを除けば、データを読み込むコードもこれまで通りです。画像表示や、識別器と生成器を実際に生成するMakeFrom関数も前回同様となっています。これらについては、後でまとめて紹介することにしましょう。なお、全体のコードはこのノートブックで公開しているので、必要に応じて参照してください。少し説明が長くなっているので、とりあえず結果だけ見たいという方はこの先まで進んでしまい、結果を見てから、ここに戻ってくるのもありでしょう。
前回までと大きく変わったのは、学習を行うtrain関数です(かなり長くなったので、もっと短い関数の集まりに書き直して読みやすくしたくもなったのですが、それは今回はやめておきましょう)。
def train(netD, netG, batch_size, zsize, epochs, trainloader):
losses_netD = []
losses_netG = []
out_D_real = []
out_D_fake = []
out_G = []
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
netD = netD.to(device)
netG = netG.to(device)
one_labels = torch.ones(batch_size).reshape(batch_size, 1).to(device)
zero_labels = torch.zeros(batch_size).reshape(batch_size, 1).to(device)
criterion = nn.BCELoss().to(device)
optD = optim.Adam(netD.parameters(), lr=0.0002, betas=[0.5, 0.999])
optG = optim.Adam(netG.parameters(), lr=0.0002, betas=[0.5, 0.999])
fixed_noise = torch.randn(8, zsize, 1, 1).to(device)
for epoch in range(1, epochs+1):
running_loss_netD = 0.0
running_loss_netG = 0.0
for count, (real_imgs, _) in enumerate(trainloader, 1):
netD.zero_grad()
# 識別器の学習
real_imgs = real_imgs.to(device)
# データローダーから読み込んだデータを識別器に入力し、損失を計算
output_real = netD(real_imgs).reshape(batch_size, -1)
loss_real = criterion(output_real, one_labels)
loss_real.backward()
# 生成器から得たデータを、識別器に入力し、損失を計算
z = torch.randn(batch_size, zsize, 1, 1).to(device)
fake_imgs = netG(z).to(device)
output_fake1 = netD(fake_imgs.detach()).reshape(batch_size, -1)
loss_fake1 = criterion(output_fake1, zero_labels)
loss_fake1.backward()
# それらをまとめたものが最終的な損失
loss_netD = loss_real + loss_fake1
optD.step()
running_loss_netD += loss_netD # 1バッチ分の損失の平均値を加算
# 生成器の学習
netG.zero_grad()
z = torch.randn(batch_size, zsize, 1, 1).to(device)
fake_imgs = netG(z).to(device)
output_fake2 = netD(fake_imgs).reshape(batch_size, -1)
loss_netG = criterion(output_fake2, one_labels)
loss_netG.backward()
optG.step()
running_loss_netG += loss_netG # 1バッチ分の損失の平均値を加算
# 最初のエポックだけ10、20、……、100バッチ終了時の学習状況を表示
if epoch == 1:
if count < 100 and count % 10 ==0:
stat1 = f'epoch: {epoch:02d}, batch: {count}\t'
stat2 = f' lossD: {loss_netD:.4f}(real: {loss_real:.4f}, fake: {loss_fake1:.4f}),'
stat3 = f'lossG: {loss_netG:.4f}, D(x): {output_real.mean():.4f},'
stat4 = f'D(G(z)): {output_fake1.mean():.4f}, {output_fake2.mean():.4f}'
print(stat1, stat2, stat3, stat4)
if count % 100 == 0: # 1エポックの中で100回ごとに学習の状況を記録
out_D_real.append(output_real.mean())
out_D_fake.append(output_fake1.mean())
out_G.append(output_fake2.mean())
stat1 = f'epoch: {epoch:02d}, batch: {count}\t'
stat2 = f' lossD: {loss_netD:.4f}(real: {loss_real:.4f}, fake: {loss_fake1:.4f}),'
stat3 = f'lossG: {loss_netG:.4f}, D(x): {output_real.mean():.4f},'
stat4 = f'D(G(z)): {output_fake1.mean():.4f}, {output_fake2.mean():.4f}'
print(stat1, stat2, stat3, stat4)
running_loss_netD /= count # 1エポック終了時にその間の損失の平均を求める
running_loss_netG /= count
losses_netD.append(running_loss_netD)
losses_netG.append(running_loss_netG)
print(f'epoch: {epoch}, running_loss_D: {running_loss_netD}, running_loss_G: {running_loss_netG}', '\n')
if epoch % 5 == 0:
generated_imgs = netG(fixed_noise).cpu()
imshow(generated_imgs.reshape(8, 3, 32, 32))
return (losses_netD, losses_netG), (out_D_real, out_D_fake, out_G), (netD, netG)
大きく変わったと書きましたが、学習中にさまざまなデータを取り出したり、表示したりする部分が増えただけで、学習を行う部分は前回と変わっていません。特に変更した部分といえるのは、二重ループの内部にある2つのif文です。
1つ目のif文では、最初のエポックを学習する際のそのまた初期に重みの変化があると想定して、1エポック目の10、20、……、100バッチまでは10個のミニバッチごとに識別器に訓練データを入力した結果「D(x)」の値と、識別器に偽データを入力した結果「D(G(z))」の値、それから識別器と生成器の損失を画面に出力するようにしています(D(G(z))は、識別器の学習と生成器の学習で2回計算するので、両者を表示しています)。
# 最初のエポックだけ10、20、……、100バッチ終了時の学習状況を表示
if epoch == 1:
if count < 100 and count % 10 ==0:
stat1 = f'epoch: {epoch:02d}, batch: {count}\t'
stat2 = f' lossD: {loss_netD:.4f}(real: {loss_real:.4f}, fake: {loss_fake1:.4f}),'
stat3 = f'lossG: {loss_netG:.4f}, D(x): {output_real.mean():.4f},'
stat4 = f'D(G(z)): {output_fake1.mean():.4f}, {output_fake2.mean():.4f}'
print(stat1, stat2, stat3, stat4)
2つ目のif文では、100バッチごとに今述べたようなデータを画面に表示するとともに、関数の戻り値として呼び出し側に渡せるようにリストにそれらを保存しています。
if count % 100 == 0: # 1エポックの中で100回ごとに学習の状況を記録
out_D_real.append(output_real.mean())
out_D_fake.append(output_fake1.mean())
out_G.append(output_fake2.mean())
stat1 = f'epoch: {epoch:02d}, batch: {count}\t'
stat2 = f' lossD: {loss_netD:.4f}(real: {loss_real:.4f}, fake: {loss_fake1:.4f}),'
stat3 = f'lossG: {loss_netG:.4f}, D(x): {output_real.mean():.4f},'
stat4 = f'D(G(z)): {output_fake1.mean():.4f}, {output_fake2.mean():.4f}'
print(stat1, stat2, stat3, stat4)
もう1つ、ループを回して学習を始める前に変数fixed_noiseに100次元の乱数を8つ保存しています。5エポックが終わるごとに、この変数に保存された値を生成器に入力して、一定の値からどんな画像が生成されるかを確認するようにしました。
fixed_noise = torch.randn(8, zsize, 1, 1).to(device)
# …… 省略 ……
for epoch in range(1, epochs+1):
# …… 省略 ……
if epoch % 5 == 0:
generated_imgs = netG(fixed_noise).cpu()
imshow(generated_imgs.reshape(8, 3, 32, 32))
以上がtrain関数の主な変更部分です。
最後に、変更したわけではないですが、損失の計算について簡単に見ておきましょう。識別器には訓練データと偽データの2つのデータが入力されますが、では、その損失はどうなるでしょうか。訓練データが入力されたときの結果(推測値)は、先ほども述べたように、D(x)と表せます。また、偽データが入力されたときの結果はD(G(z))となります。前者については、「訓練データが入力された」ことを「1」とすれば、D(x)と1を損失関数に渡すことで損失が得られます。後者については「偽データが入力された」ことを「0」とすれば、D(G(z))と0を損失関数に渡すことで損失が得られます。そして、それらを足し合わせたものが識別器の全体としての損失となります。このようにすることで、識別器の重みの更新が「訓練データが入力されたら1を出力」「偽データが入力されたら0を出力」という方向で行われるはずです。
一方、生成器の学習では、偽データを識別器に入力した結果「D(G(z))」を「1」と比較しています。これはPyTorchのDCGANのチュートリアルなどを読むと、ちょっとしたテクニックとなっているようですが、直観的には「生成器の学習では、D(G(z))が1となる方向で重みを更新できるように損失を計算する」と考えてもよいかもしれません。
今回は、この損失の計算にPyTorchのBCELoss関数を使っています。
criterion = nn.BCELoss()
# …… 省略 ……
output_real = netD(real_imgs).reshape(batch_size, -1)
loss_real = criterion(output_real, one_labels)
ここでBCELoss関数がどんな値を返すのかを極端な例で示しておきます。そうすれば、この関数が実際にどんなふうに損失を計算しているかを何となく分かるかもしれません。
criterion = torch.nn.BCELoss()
ones = torch.ones(8) # 訓練データが入力されたことを表す
zeros = torch.zeros(8) # 偽データが入力されたことを表す
t1 = torch.ones(8) # 識別器に何かのデータを入力したら全て1という値になった
t0 = torch.zeros(8) # 識別器に何かのデータを入力したら全て0という値になった
print(criterion(t1, ones)) # tensor(0.)
print(criterion(t0, zeros)) # tensor(0.)
print(criterion(t1, zeros)) # tensor(100.)
print(criterion(t0, ones)) # tensor(100.)
この例では、変数onesには学習時に訓練データが識別器に入力されたとして、その結果と比較するための全要素が1となっているテンソルが格納されています。変数zerosにはその逆に偽データが入力されたことを意味する全要素が0のテンソルが格納されています。変数t1とt0には、識別器からの出力を模した値が格納されています。これらを、BCELoss関数で比較してみた結果、t1とonesの比較、t0とzerosの比較では結果は0となっています(損失0)。t1とzerosの比較、t0とonesの比較では結果は100になっています。
識別器からの出力は0〜1の値となるので、それらを0または1と比較した結果は上の通り、0〜100の範囲になります(深くは説明しませんが、PyTorchのBCELoss関数ではlog 0は-100となるようにすることで、エラーが発生しないようにしています)。大ざっぱな言い方をすれば、識別器からの出力が想定と異なる値になったときには100に近い値が、想定に近い値であれば0に近い値が返されると考えましょう。
というわけで、次に実際のDCGANを学習させて、識別器からの出力であるD(x)、D(G(z))の値や損失関数に注目してみましょう。
シンプルなバージョン
まずは前回も作成したConv2dクラスとConvTranspose2dクラスと活性化関数だけで構成される識別器と生成器で試してみます。生成器と識別器は次のような構造になっています。
discriminator = nn.Sequential(
nn.Conv2d(3, 64, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64, 128, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(128, 256, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(256, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
)
feature_maps = 64
zsize = 100
generator = nn.Sequential(
nn.ConvTranspose2d(zsize, feature_maps * 8, 4, 1, 0, bias=False),
nn.ReLU(inplace=True),
nn.ConvTranspose2d(feature_maps * 8, feature_maps * 4, 4, 2, 1, bias=False),
nn.ReLU(inplace=True),
nn.ConvTranspose2d(feature_maps * 4, feature_maps * 2, 4, 2, 1, bias=False),
nn.ReLU(inplace=True),
nn.ConvTranspose2d(feature_maps * 2, 3, 4, 2, 1, bias=False),
nn.Tanh()
)
netD = MakeFrom(discriminator)
netG = MakeFrom(generator)
EPOCHS = 80
losses, outs, nets= train(netD, netG, batch_size, zsize, EPOCHS, trainloader)
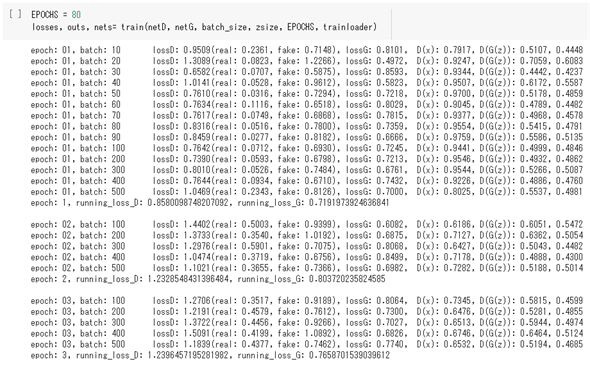
この実行結果の最初の部分を示します。
出力の右側には、「D(x) 」と「D(G(z)) 」という出力があります(D(G(z))は2つの値が表示されていることに注意)。繰り返しになりますが、D(x)は識別器に訓練データを入力した結果でした。よって、その値は「訓練データが入力された」ことを意味する「1」に近い値となるのが理想的です。一方、D(G(z))は100次元の乱数を生成器に入力して得られた偽データを識別器に入力した結果です。ということは、こちらの理想的な値は「偽データが入力された」ことを意味する「0」に近い値だと考えられます。これを踏まえて、出力を見ていきましょう。
D(x)については1に近い値が表示された後、次第に値が低くなっていくことが分かります。これは学習が進む中で、訓練データを入力した場合でも、偽データが入力されたと識別器が判断することが多くなったのだと推測されます。
D(G(z))については、最初に0.5近辺の値が続いています。これは識別器の学習がそれほど進んでいないためにどっちつかずの値が出力されているのでしょう。その後も値がそれほど変わらない理由は不明です(何らかの理由で最適化がこれ以上は進まなくなってしまったのかもしれませんし、そのスピードがとても遅いのかもしれません。あるいは別の理由があるかもしれません)。
識別器の損失(lossD)はかっこ内のrealとfakeの和です。realはD(x)の値が大きければ小さな値となります(識別器が正しい判定をした)。fakeはD(G(z))の1つ目の値が小さければ小さな値となります(識別器が正しい判定をした)。生成器の損失はD(G(z))の2つ目の値が大きければ小さくなります(生成器が識別器をだませた)。
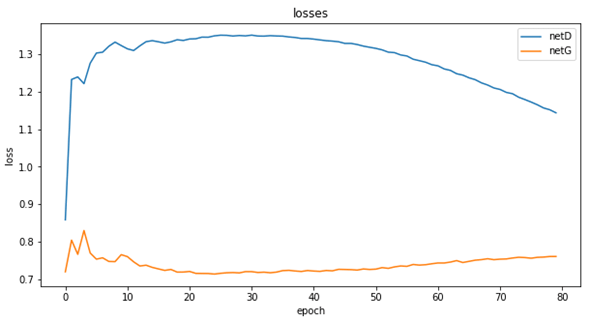
学習を通した損失がどのようになっているかを以下に示します。
このニューラルネットワークモデルでは、識別器の損失(青色の線)は最初にギュッと上がった後に緩やかに低下していっています。今回は80エポックの学習でしたが、もう少し学習すると損失はまだ下がっていたかもしれません。生成器の損失(オレンジ色の線)は初期に少し上がった後は緩やかに低下して、最後にまた上昇しています。これは、識別器の学習が進み(緩やかに損失が低下)、生成した画像がニセモノだと判定されている確率が少しずつ上がっているということでしょう。
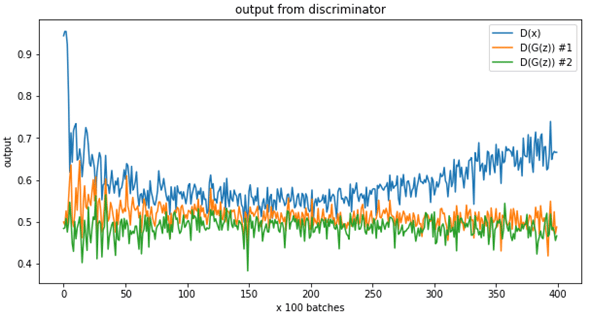
最後にD(x)、D(G(Z))の値の推移を以下に示します。
D(x)は訓練データをきちんと訓練データと識別できたかどうかを表す値です(青色の線)。学習初期には少しずつ低下していますが、後半に上昇基調となっているのは、上の損失関数のグラフで損失が低下した辺りとリンクしているようにも見えます。D(G(z))の2つの値は、最初はブレが大きくなっていますが、次第にその幅が狭まっていますね。これは識別器の精度がある程度上がっているのだと考えられるかもしれません。
最後に、80エポックを学習した後に変数fixed_noiseの値を基に生成された画像を以下に示します。
筆者の目には左から「動物か乗り物のような何か」「犬?」「何か」「建物」「建物」「飛行機?」「飛行機的な何か」「ピザ」のように見えます。が、CIFAR-10にこんな画像ありそうだとは思いませんか?(思いませんね)。
Copyright© Digital Advantage Corp. All Rights Reserved.