［データ分析］平均値の落とし穴 〜 平均給与が高すぎる？！：やさしいデータ分析
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第3回。分布の中心的な位置を表す値として代表値を取り上げ、尺度や分布によって適切な代表値を利用する必要があることを説明します。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第3回です。前回はデータ分析の進め方について見た後、オープンデータを利用した分析の方法を簡単に紹介しました。今回は、引き続き、分布の中心的な位置を表す値として代表値を取り上げます。代表値の求め方だけでなく、尺度や分布により、適切な代表値を利用する必要があることを説明します。なお、分布とはデータの散らばり具合、つまり、どのような値がどのような位置にどれだけあるかということです。
連載：
この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト（ExcelやGoogleスプレッドシート）を利用した作成例を紹介します。
必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
羽山博筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入（またもや金欠）。
サンプルファイルの利用について
本稿では、表計算ソフトを使って手を動かしながら学んでいきます。そこで、表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントがあれば使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントがあれば使える無料のGoogleスプレッドシート（Google Sheets）をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、.xlsxファイルをGoogleドライブにアップロードしてから開いた上で［ファイル］メニューの［Google スプレッドシートとして保存］を実行してください。
代表値として最もよく使われる平均値、でも万能ではない
私たちが小学校の算数や理科で学んだ平均値は、算術平均または相加平均と呼ばれるもので、全ての値を足して、個数で割れば求められます。しかし、Excelなどの表計算ソフトではそういった計算を行わなくても、AVERAGE関数を利用すれば簡単に平均値が求められます。
では、ウオーミングアップがてら、セルB2〜B1001に入力されている「勤め先収入」の平均値をセルD2に求めてみてください（図1）。単位は万円です。サンプルファイル（03a.xlsx）はこちらからダウンロードできます。ここでは、Windows 11上で、Microsoft 365（Excel 2019以降）のデスクトップ版を使って説明を行いますが、Microsoft 365オンライン版やGoogleスプレッドシートを利用する場合はこのページの上の「サンプルファイルの利用について」に示した方法でサンプルファイルをOneDriveやGoogleドライブにアップロードしてからご利用ください。入力する関数はいずれも同じです。
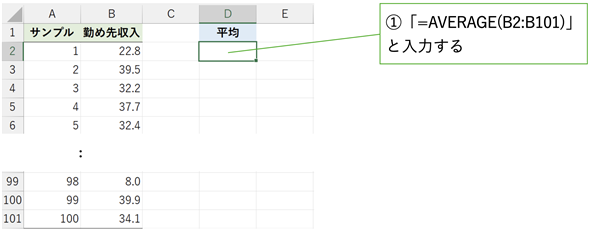図1 勤め先収入の平均値を求めてみるセルD2に「=AVERAGE(B2:B101)」と入力して平均値を求めよう。データは架空のものだが、勤労者世帯の勤め先収入の平均値（月49.2万円）と一致するように作成してある。平均値の出典は、総務省統計局の家計調査の統計表に掲載された2022年の値（※左記のリンクをクリックするとs01.xlsxファイルがダウンロードされます）。
答えは簡単、セルD2に「=AVERAGE(B2:B101)」と入力するだけです。基本の基本とも言える関数ですが、形式と説明をこの記事の最後にまとめておきます（以降、初出の関数名にリンクを設定しており、リンク先で形式と説明が見られるようにしておきます。リンク元に戻るにはWebブラウザーの［戻る］ボタンを使用してください）。
49.2という結果が得られたでしょうか。ダウンロードしたファイルには答えのワークシートも含まれているのでそちらもご参照ください（具体的には、表計算ソフトの下部にある［平均値を求める（答え）］をクリックしてください）。
なお、具体的な操作については、これ以降の例も含めて動画で説明しています。データ量が100件とかなり多いので、できるだけ効率よく操作を行いたいものですね。効率のよい方法を知りたい方は、ぜひご視聴ください。
動画1 Excelで平均値／中央値／最頻値を求める
さて、平均値を求めたところで、毎月の勤め先収入が月49.2万円もあるのは納得できないと思った方も多いのではないでしょうか（ま、そんなもんだろう、と思われる方もおられるかもしれませんが、少なくとも筆者はそんなにもらっていません……ちょっと話がそれますが、人それぞれに暗黙のうちに持っている基準と比較しているので、感じ方も人それぞれです。例えば、「月12.3万バーツ」だと言われると、バーツという通貨を日常的に使っていない人には高いのか安いのか判断できません。分析に当たっては、基準となる値や他の値と比較することが重要になってくるのですが、それについてはまた回を改めてお話します）。
話を元に戻しましょう。平均値は代表値としてよく使われる便利な値ですが、場合によっては実態を反映していないこともあります。実は、上で見た例では、収入が月100万円を超える人が3人いて、その中にはなんと月1,600万円という人もいます。このような外れ値と呼ばれる極端に大きな値（や小さな値）がデータに含まれていたり、分布（データの散らばり具合）に偏りがあると、平均値が代表値としてふさわしくないことがあります。
外れ値を見つけることはデータ分析においてとても重要なことです。上の例にある1,600万円という値に関しては、実際にそれだけの収入がある人がいるかもしれませんし、入力ミスなのかもしれません。分析の精度を上げるために、外れ値を除外して分析を行うこともあります。
ちなみに、TRIMMEAN関数を使えば、上下合わせて何パーセントかの値を除外した平均値が求められます。例えば「=TRIMMEAN(B2:B101,10%)」と入力すれば、上位5％と下位5％を除外した平均値が求められます（31.1万円になります）。
極端な値や分布の偏りに影響されにくい中央値
外れ値がある場合や、分布に偏りがある場合には、平均値の代わりに、中央値を代表値として使うこともよくあります。中央値（メディアン）とは、値を小さい順に並べたときに、ちょうど真ん中にある値のことです。データの件数が偶数個の場合、真ん中の値が2つありますが、そのときはそれらの値の平均値を中央値とします。
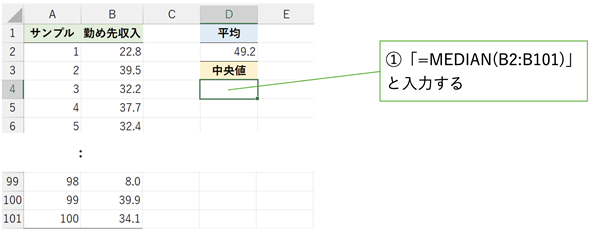
Excelなどの表計算ソフトでは、MEDIAN関数に値を指定すれば簡単に中央値が得られます。先ほどダウンロードしたサンプルファイル（03a.xlsx）のワークシート［中央値を求める］を開いてください。セルD3に「中央値」という見出しがあります。セルD4にMEDIAN関数を入力してみましょう（図2）。結果は31.4になるはずです。
あくまで上のデータは架空データなので、ここで求めた値が勤労者世帯の実情を正しく反映しているわけではありませんが、一般に、給与や収入に関しては分布に偏りがあり、一部の大きな値に引きずられて平均値が大きくなっていると言われています。その場合、中央値＜平均値となります。実情はさておき、このデータに関する限り、平均値の49.2万円より中央値の31.4万円の方が代表値として納得できる値と言えるでしょう。
尺度によって代表値が異なる 〜 平均値／中央値／最頻値の使い分け
私たちは平均値にあまりにも慣れ親しんでいるので、何でも平均値を基準に考えてしまう「平均値信仰」とでも言ったようなものに取りつかれている傾向があります。しかし、平均値がアテにならないこともある、というのは上で見た通りです。
加えて、代表値として使える値は尺度によって異なるということも理解しておきましょう（表1）。尺度については、前回解説しました。
| 尺度 | 利用できる代表値 | データの例 |
|---|---|---|
| 間隔尺度、比率尺度 | 平均値 | 身長、体重、反応時間など |
| 順序尺度 | 中央値 | ランキングの順位、5段階評価など |
| 名義尺度 | 最頻値 | 製品名、好きなスポーツの種類など |
間隔尺度なら平均値、順序尺度なら中央値、名義尺度なら最頻値を代表値として使う。以下の説明にあるように、上の方に記した尺度では、下の方に示した代表値も使える。
今回の勤め先収入の例であれば、間隔尺度なので平均値を使えばいいということが分かります。基本的に表1の上の方に記した尺度では、下の方に記した代表値も使えます。例えば、分布に偏りのある間隔尺度のデータであれば、中央値や最頻値（後述します）が使えます。しかし、その逆はできません。例えば、名義尺度の代表値として平均値や中央値を使うことはできません。ただし、順序尺度の場合、本来は中央値または最頻値を使いますが、5段階評価などの場合、分布に偏りがなければ、便宜的に間隔尺度と見なして平均値を使うこともあります。
最もよく現れる値も代表値として使える 〜 最頻値
では、代表値の3番手として登場した最頻値について見てみましょう。最頻値とは、最もよく現れる値のことです。
Excelなどの表計算ソフトでは、最頻値はMODE.SNGL関数またはMODE.MULT関数で求められます。最頻値が複数ある場合、MODE.SNGL関数は最初に現れた最頻値を返しますが、MODE.MULT関数は全ての最頻値を返します。
では、余暇に行うスポーツのデータを使ってセルD4に最頻値を求めてみてください。ここではMODE.SNGL関数を使うものとします（図3）。サンプルファイル（03b.xlsx）はこちらからダウンロードできます。データはセルB4〜B1003に入力されています。
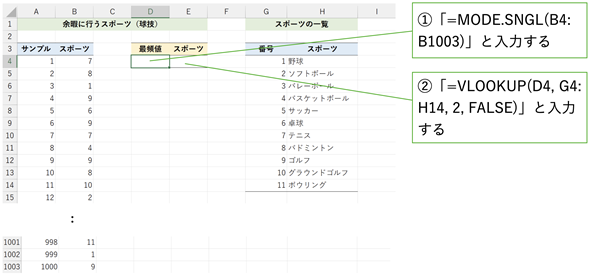図3 余暇に行うスポーツの最頻値を求めてみるセルD4に「=MODE.SNGL(B4:B1003)」と入力して最頻値を求めてみよう。このデータは、総務省統計局の社会生活基本調査（2021年）から球技だけを取り出して、同じ比率になるように加工したもの。スポーツの種類は［スポーツの一覧］表の［番号］列に数値で表されているが、この数値は単に種類を区別するためだけの、名義尺度のデータ。
最頻値として、9という値が得られれば正解です。
9は「ゴルフ」を表しますが、結果が数字で表示されるだけだと分かりにくいので、スポーツの名前も表示できるようにしてみましょう。そのために、VLOOKUP関数を使って、セルE4に「=VLOOKUP(D4,G4:H14,2,FALSE)」という式を入力します。もしくはMicrosoft 365で使えるXLOOKUP関数を使って、セルE4に「=XLOOKUP(D4,G4:G14,H4:H14,"",0,1)」と入力しても同じ結果が得られます。いずれの関数も、検索値（この場合は9）を基に表（この場合は［番号］列と［スポーツ］列を持つ［スポーツの一覧］表）を検索し、対応する値（この場合は「ゴルフ」）を取り出すためのものです。
余談ですが、上の調査は5年に1度行われており、前回の社会生活基本調査（2016年）では、球技の最頻値はボウリングでした。ボウリングがゴルフに首位を明け渡したのは、2019年以降のコロナ禍の影響で屋内でのスポーツができなくなったという要因があるのかもしれません（引用元のデータを見ると、全体的に屋内のスポーツが減少していることも分かります）。
度数分布表も作っておこう 〜 COUNTIF関数を使う
9番の「ゴルフ」が最頻値であるということは分かりましたが、1000人のうち、9番と答えた人は何人いるのでしょうか。そこで、それぞれのスポーツについて、度数（データが幾つあるか）を一覧にした表を作ってみましょう。そのような表を度数分布表と呼びます。
この例では、条件付きで個数を数えるので、COUNTIF関数を使います。引数には、データの範囲と条件を指定します。先ほどダウンロードしたサンプルファイル（03b.xlsx）のワークシート［度数分布表を作成する］を開いて、各［番号］に対する度数をセルI4〜I14に求めてみましょう（図4）。なお、度数分布表の作成についても、動画で操作方法を説明しています。動画を見ながら1つ1つ操作を丁寧に追いかけたい方は、ぜひご視聴ください。
動画2 Excelで度数分布表を作成する
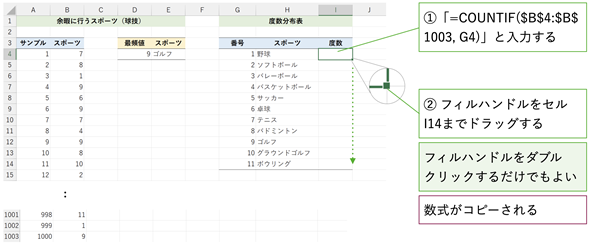図4 余暇に行うスポーツの度数分布表を作るセルI4に「=COUNTIF($B$4:$B$1003,G4)」と入力すれば、セルB4〜B1003の範囲で、セルG4の値（1）と一致するデータの個数が求められる。セルE4の右下に表示されているフィルハンドル（小さな■）をセルI14までドラッグすれば、数式がコピーされ、全ての値が求められる。なお、フィルハンドルをダブルクリックすると、隣接するセルにデータが入力されているところまで数式がコピーされる。コピーする行数が多いときにはフィルハンドルのダブルクリックが便利。
データの範囲であるB4:B1003の列番号と行番号の頭に「$」を付け、「$B$4:$B$1003」としてあります。このように、列番号や行番号の頭に「$」を付けてセル参照を表す方法を絶対参照と呼びます。絶対参照の場合、数式をコピーしてもセル参照は変わりません。
一方、条件を表すために指定した「G4」のような（頭に$を付けない）セル参照は相対参照と呼ばれます。相対参照の場合、数式をコピーするとコピーした方向に合わせて数式中のセル参照が変わります。この例では下方向にコピーするので、G4はG5、G6……と行番号が増えていきます（図5）。
図5 数式をコピーする（絶対参照と相対参照の違い）絶対参照の場合、数式をコピーしても数式中のセル参照は変わらない。相対参照の場合、数式を下方向にコピーするとセル参照の行番号が増え、右方向にコピーすると列番号が増えていく。
「相対参照だとコピーしたときにセル参照が変わる」ということは、Excelの基本なので、すでにご存じの方も多いと思います。しかし、「コピーしたときにセル参照が変わるのが相対参照」と言うと、語弊があります。そもそも、相対参照とは現在のセルから見てどの位置にあるかというセル参照の表し方を意味します。
例えば、セルI4に入力した「=COUNTIF($B$4:$B$1003,G4)」に含まれる「G4」は、セルI4から見て「1つ左の列で同じ行」ですね。そのセル参照を含んだ数式をセルI5にコピーすると「=COUNTIF($B$4:$B$1003,G5)」になりますが、この「G5」はやはりセルI5から見て「1つ左の列で同じ行」です。コピーしたときに列番号や行番号が変わるのはあくまでも結果としてそうなるだけのことで、単に「1つ左の列で同じ行」というセル参照がコピーされているだけなのです。
Excelのオプションで、数式の表示方法をR1C1形式に変更すると、そのことがよく分かるのですが、話が本筋から外れてしまうので、これ以上は触れないことにします。
なお、Microsoft 365（Excel 2019以降）には「スピル」と呼ばれる機能が備わっており、セルI4に「=COUNTIF(B4:B1003,G4:G14)」と入力して［Enter］キーを押すだけで（数式をコピーしなくても）、全ての結果が求められます。スピル機能の働きにより、1つの数式だけで複数の結果が得られるというわけです。
Googleスプレッドシートでは、セルI4に「=ArrayFormula(COUNTIF(B4:B1003,G4:G14))」と入力します。なお、Excel 2016以前では、スピル機能が使えないので、図5のように数式をコピーするか、数式を配列数式として入力すれば、全ての結果が得られます。配列数式を入力するには、あらかじめ結果を表示したいセル範囲を選択しておき、（数式バーではなく）選択したセル範囲の最初のセルに対して「=COUNTIF(B4:B1003,G4:G14)」と数式を入力し、入力の終了時に［Enter］キーではなく、［Ctrl］＋［Shift］＋［Enter］キーを押します。ただし、この連載ではスピル機能が使えるものとして話を進めます。
間隔尺度の最頻値は度数分布表を作って求める 〜 FREQUENCY関数を使う
間隔尺度のデータでは、ほとんどの値が1回〜数回しか現れないので、MODE.SNGL関数やMODE.MULT関数を使ってデータの個数を数えても最頻値は求められません。例えば、最初に見た勤め先収入の場合、24.9という値が最も多く現れますが、たったの3回だけです。
そこで、間隔尺度の場合は、データを一定の幅で区切って、その範囲に入る値の数を数えて度数分布表を作ります。その値の範囲を階級と呼びます。
もう少し正確に言うと、離散値（スポーツの種類を表す値や5段階評価のように、値が飛び飛びになっているもの）で、現れる値の種類が少ない場合には、MODE.SNGL関数やMODE.MULT関数を使って最頻値を求めます。一方、連続値（身長や体重など範囲内でどのような値でも取れるようなもの）で、現れる値の種類が多い場合には、度数分布表を作って最頻値を求めます。
では、勤め先収入の例で見てみましょう。度数分布表の作成にはFREQUENCY関数が便利です。サンプルファイル（03c.xlsx）はこちらからダウンロードできます。サンプルファイルを開いて、各階級の度数をセルF6〜F13に求めてみましょう（図6）。
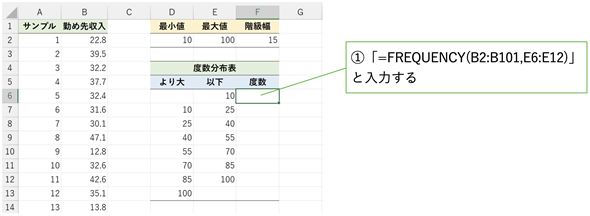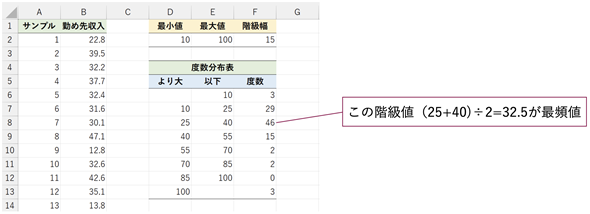
図6 階級を設定して度数分布表を作るセルD6〜セルE13で階級を設定している。ここでは、階級の幅を15とし、10以下の小さな値と、100より大きな値をひとまとめにした（階級数は8となる）。セルF6に「=FREQUENCY(B2:B101,E6:E12)」と入力すれば、度数分布表が作成できる。
FREQUENCY関数には、データの範囲と階級の範囲を指定します。階級としては「以下」を表すデータの並びを指定します。ただし、最後の階級（セルE13）は指定しなくて構いません。スピル機能により、1つの数式で全ての結果が求められます（図7）。
度数分布表から、25万円より大きく、40万円以下という階級に46人いることが分かりました。この最も度数の大きい階級値を最頻値とします。階級値は階級の（下限＋上限）÷2で求めます。つまり、（25＋40）÷2＝32.5が最頻値となります。度数の46が最頻値ではないことに注意してください。
なお、度数分布表はCOUNTIF関数やCOUNTIFS関数を使ってデータの個数を数えることによって作成することもできます。サンプルファイル（03c.xlsx）のワークシート［度数分布表を作成する（COUNTIFS)］にはその例も含めてあります。
階級数の決め方 〜 スタージェスの公式
補足ですが、階級数を幾つにするかは、スタージェスの公式と呼ばれる以下の式で求めた値が目安になります。nはサンプルサイズ（得られたデータの個数）です。
上の例であれば、サンプルサイズが100なので1＋log2100≈7.6となります。Excelなどの表計算ソフトで計算するならLOG関数を使って「=1+LOG(100,2)」という数式を入力すれば求められます。この値はあくまで目安ですが、図6や図7ではこの公式で求めた結果を基に、階級数を8としています。
コラム どの代表値も使えない？！ 〜 複数の集団が混在している場合
代表値は分布の中心的な位置を表す便利な値ですが、半面、落とし穴もあります。すでに述べたように、外れ値がある場合や分布に偏りがある場合、平均値が代表値としてはふさわしくないといったことなどです。従って、代表値を求める前には、分布を見ることが重要です。
分布は度数分布表でも確認できますが、ヒストグラム（度数分布表をグラフ化したもの）を作成すると、その特徴がよく分かります。以下の図8の例は勤め先収入の特徴をもう少し細かく見るために、階級の幅を5としてヒストグラムにしたものです。グラフを使った可視化の方法については、回を改めて紹介するので、ここでは結果だけを示します。
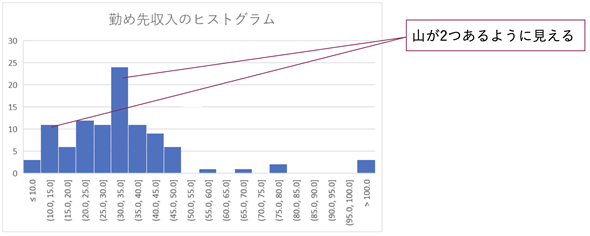図8 ヒストグラムにより度数分布表を可視化するヒストグラムは、棒グラフの棒同士の間隔を詰めたものと考えればよい。このグラフを見ると、30万円〜35万円に大きな山があるが、10万円〜15万円にも小さな山があるように見える。このような場合、複数の異なる集団のデータがまとめられている可能性がある。
実を言うと、このデータは、あえて10万円〜15万円のところと、30万円〜35万円のところに山ができるように作ったものです。つまり比較的収入の少ない集団と、そうでない集団とが混在しているというわけです。このような場合、それぞれの集団の分布に偏りがないとしても、それらの集団をまとめて求めた代表値は、全体を「代表」するのにふさわしい値ではないということになります。この例では、中央値が31.4万円で、大きな山のある階級に含まれるので、問題はなさそうに思われますが、その数値だけに頼ると、収入の少ない人たちを見失いがちになります（あくまで架空のデータですが）。
極端な例も紹介しましょう。ある公園の利用者の平均年齢が30歳だったとします。では、30歳に近い人たちに合わせて公園を整備するのが最適な施策なのでしょうか。その公園の利用者が小学生と老人ばかりだったとすると、平均年齢は30歳であっても、実際には30歳に近い人はほとんどいないことになります。極端すぎて、そんな落とし穴にひっかかる人はいないだろうと思われるかもしれませんが、ターゲットを見誤ったために閑古鳥が鳴いている施設の例などを身近に見聞きしたことのある方も多いのではないでしょうか。
今回は、集団の代表値として利用される平均値、中央値、最頻値の意味や性質、分布や尺度による取り扱いの違いなどについて、Excelを使いながら具体例を見てきました。また、代表値を求めるに先立って、分布を見ることが重要であるというお話もしました。
次回は、集団の分布に関して、「散らばり具合」を表す値（分散／標準偏差、四分位範囲、平均情報量）を求める方法を尺度ごとに紹介します。では、次回もお楽しみに！
関数リファレンス： この記事で取り上げた関数の形式
関数の使いこなし方については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
代表値を求めたり、度数分布表を作ったりするために使った関数
AVERAGE関数： 平均値（算術平均）を求める
形式
AVERAGE(数値1, 数値2, ... , 数値255)
引数
- 数値： 平均値を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。
TRIMMEAN関数： 上下何パーセントかを除外した平均値（刈り込み平均）を求める
形式
TRIMMEAN(配列, 除外する割合)
引数
- 配列： 平均値を求めたい数値の並びやセル範囲を指定する。
- 除外する割合： 上下合わせて何パーセントを除外したいかを指定する。例えば、10%を指定すると、上位5％と下位5％の値を除外した平均が求められる。10%の代わりに、0.1と指定してもよい。
MEDIAN関数： 中央値を求める
形式
MEDIAN(数値1, 数値2, ... , 数値255)
引数
- 数値： 中央値を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。
MODE.SNGL関数, MODE.MULT関数： 最頻値を求める
形式
MODE.SNGL(数値1, 数値2, ... , 数値254)
MODE.MULT(数値1, 数値2, ... , 数値254)
※MODE.SNGL関数は最初に見つけた最頻値を返し、MODE.MULT関数は全ての最頻値を返す。
引数
- 数値： 最頻値を求めたい数値やセル範囲を指定する。引数は254個まで指定できる。
COUNTIF関数： 1つの条件に一致するデータの個数を数える
形式
COUNTIF(範囲, 検索条件)
引数
- 範囲： 検索するデータの範囲を指定する。
- 検索条件： 検索条件を文字列として指定する。例えば、「">=10"」と指定すれば「10以上」という意味になる。特定の値と一致するという条件であれば、値をそのまま書いてもよい。例えば、「"=10"」でも、単に「10」と指定しても「10と一致する」という意味になる。
FREQUENCY関数： 度数分布表を作成する
形式
FREQUENCY(配列, 区間配列)
引数
- 配列： 度数分布表の基となる数値の並びやセル範囲を指定する。
- 区間配列： 各階級の上限を表す数値の並びやセル範囲を指定する。最後の階級の上限は指定しなくてもよい。
表を見やすくするために、または参考として取り上げた関数
VLOOKUP関数： 検索値を基に表を検索し、対応する値を取り出す
形式
VLOOKUP(検索値, 範囲, 列番号, 検索方法)
引数
- 検索値： 検索したい値を指定する。
- 範囲： 検索値を検索する表の範囲を指定する。表の左端の列が検索される。
- 列番号： 検索値が見つかったときに取り出したい値の列番号を指定する。
- 検索方法： 以下の値を指定する。
- TRUEまたは省略 …… 近似値検索。近似値検索の場合、検索値以下の最大値が検索される。
- FALSE …… 完全一致検索。
XLOOKUP関数： 検索値を基に表を検索し、対応する値を取り出す
形式
XLOOKUP(検索値, 検索範囲, 戻り範囲, 見つからない場合の値, 一致モード, 検索モード)
引数
- 検索値： 検索したい値を指定する。
- 検索範囲： 検索値を検索する範囲を指定する。
- 戻り範囲： 検索値が見つかったときに、対応する値を取り出したい範囲を指定する。
- 見つからない場合の値： 検索値が見つからなかったときに返す値を指定する。
- 一致モード： 以下の値を指定する。
- 0または省略 …… 完全一致検索。
- -1 …… 近似値検索。検索値以下の最大値が検索される。
- 1 …… 近似値検索。検索値以上の最小値が検索される。
- 2 …… ワイルドカード検索（検索文字列に含まれる*を任意の文字列、?を任意の1文字として検索する）。
- 検索方法： 以下の値を指定する。
- 1または省略 …… 先頭から検索する。
- -1 …… 末尾から検索する。
- 2 …… 昇順に並べ替えられた範囲を二分検索する（効率のよい検索が行われる）。
- -2 …… 降順に並べ替えられた範囲を二分検索する（効率のよい検索が行われる）。
COUNTIFS関数： 複数の条件に一致するデータの個数を数える
形式
COUNTIF(範囲1, 検索条件1, 範囲1, 検索条件1, ..., 範囲127, 検索条件127)
引数
- 範囲： 検索するデータの範囲を指定する。
- 検索条件： 検索条件を文字列として指定する。指定の方法はCOUNTIF関数と同じ。範囲と検索条件のペアは127個まで指定でき、全ての条件を満たしたデータの個数が返される。
LOG関数： 対数を求める
形式
LOG(数値, 底)
引数
- 数値： 対数を求めたい値（真数）を指定する。
- 底： 対数の底を指定する。省略すると10が指定されたものと見なされる。
Copyright© Digital Advantage Corp. All Rights Reserved.
ITmediaはアイティメディア株式会社の登録商標です。