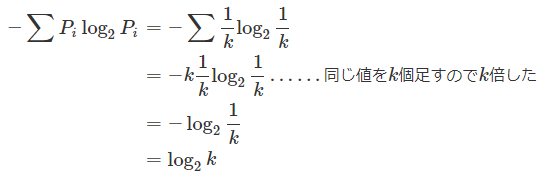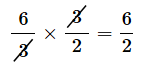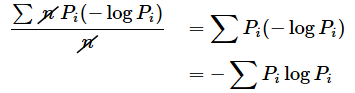［データ分析］四分位範囲と平均情報量 〜 趣味や好みにはどれぐらいの幅があるのか？！：やさしいデータ分析
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第5回。分布のばらつきの度合いを表す値として散布度を取り上げ、尺度や分布によって適切な散布度を利用する必要があることを説明します。順序尺度の散布度として使われる四分位範囲と、名義尺度の散布度として使われる平均情報量のお話です。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第5回です。前回は分布のばらつきの度合いを表す値として、間隔尺度や比率尺度のデータで使われる分散／標準偏差について、Excelの関数を使った値の求め方や、その意味について説明しました。今回は、順序尺度のデータで使われる四分位範囲（または四分位偏差）と、名義尺度のデータで使われる平均情報量（または相対情報量）を取り上げます。
連載：
この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト（ExcelやGoogleスプレッドシート）を利用した作成例を紹介します。
必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
羽山博筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入（またもや金欠）。
サンプルファイルの利用について
本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントがあれば使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントがあれば使える無料のGoogleスプレッドシート（Google Sheets）をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、.xlsxファイルをGoogleドライブにアップロードしてから開いた上で［ファイル］メニューの［Google スプレッドシートとして保存］を実行してください。
順序尺度や分布に偏りのある間隔尺度の散布度 〜 四分位範囲／四分位偏差
分布のばらつきの度合いを表す値として散布度が利用されることと、尺度によって利用できる散布度が異なることについては前回もお話ししました。おさらいもかねて、代表値と散布度の一覧（表1）を再掲しておきます。
| 尺度 | 利用できる代表値 | 利用できる散布度 | データの例 |
|---|---|---|---|
| 間隔尺度・比率尺度 | 平均値（算術平均） | 分散／標準偏差 | 身長、体重、反応時間など |
| 順序尺度 | 中央値 | 四分位範囲／四分位偏差 | ランキングの順位、五段階評価など |
| 名義尺度 | 最頻値 | 平均情報量／相対情報量 | 製品名、好きなスポーツの種類など |
間隔尺度や比率尺度なら分散または標準偏差、順序尺度なら四分位範囲（または四分位偏差）、名義尺度なら平均情報量（または相対情報量）を散布度として使う。上の方に記した尺度では、下の方に記した散布度も使える。
今回は順序尺度や分布に偏りのある間隔尺度で使われる四分位範囲／四分位偏差から見ていきます。まず、四分位範囲のイメージをつかみましょう。ざっくり言うと、データを小さい方から順に並べたときに、全体の1/4から3/4にあたる範囲が四分位範囲です。図1をご覧ください。これは、平成29（2017）年告示の中学校学習指導要領（PDF）で取り上げられている四分位範囲の定義です。
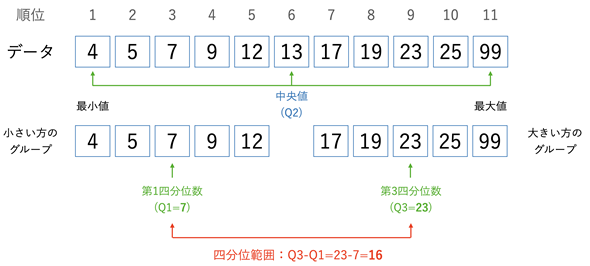図1 四分位範囲とは（中央値を除外する方法）全体を半分に分け、中央値を求める。次に、中央値より小さな値のグループと、中央値より大きな値のグループを作る。つまり、中央値を除外してグループを分ける。データが偶数個の場合はちょうど真ん中の値がないが、その場合は中央にある2つの値を除外する。次に、小さいグループの中央値を求める。これが第1四分位数（Q1）となる。また、大きいグループの中央値が第3四分位数（Q3）となる。データが偶数個の場合は、中央にある2つの値の平均をQ1やQ3とする（全体の中央値であるQ2についても同様）。Q3-Q1が四分位範囲の値となる。
データを小さい方から順に並べて4つに区切ったとき、最初の区切り位置にある値を第1四分位数と呼びます。また、3番目の区切り位置にある値を第3四分位数と呼びます。具体的な値の求め方は図1に示した通りです。ただ、いちいち第何四分位数と言うのは面倒なので、第1四分位数を「Q1」、第2四分位数を「Q2」というように簡単に表すこともよくあります。ちなみに、第2四分位数（Q2）は中央値です。
四分位範囲とは、第1四分位数（Q1）から第3四分位数（Q3）までの範囲のことで、その値は、第3四分位数（Q3）− 第1四分位数（Q1）で求められます。つまり、四分位範囲は、中央値を中心として、全体の半分程度の個数のデータがどの範囲にあるかということを表します。四分位範囲はIQR（「Inter Quartile Range」の略）とも呼ばれます。
四分位偏差は四分位範囲の値を2で割った値です。四分位偏差は中央値からの平均的なばらつきの大きさを表しています。
実は、四分位数にはさまざまな定義があります。図2のように、中央値を除外せずに分けていく方法もその一つです。
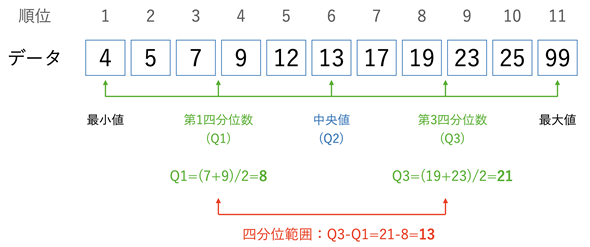図2 四分位範囲とは（中央値を含める方法）全体を半分に分け、中央値を求める。次に、中央値以下の小さな値のグループと中央値以上の大きな値のグループを作る。つまり、中央値を含めてグループを分ける。ただし、データが偶数個の場合、中央値がデータの中にないので、中央値を含めずにグループを分ける。
実は、……ちゃぶ台をひっくり返すようですが、Excelではこれらの方法とは異なる計算方法が使われます。なにっ、今までの話はなんだったんだ、と思われるかもしれませんが、実際のところ、データ数が多くなればどの方法を使ってもそれほど差が出ません。また、ばらつきの程度を把握するという意味では実用上の問題はありません。これまでのお話は四分位数や四分位範囲、四分位偏差の考え方を知るためのお話ということで、次に、Excelを使って実際に値を求めてみましょう。
四分位範囲／四分位偏差を求めてみよう（1） 〜 QUARTILE.EXC関数を使う
Excelでは、四分位数を求める関数としてQUARTILE.EXC関数とQUARTILE.INC関数が利用できます。それぞれ「クォータイル・エクスクルーシブ」「クォータイル・インクルーシブ」と読みます。先ほども述べたように、これらの関数では、図1や図2の方法とは異なる方法で四分位数が求められます。が、その方法を知らなくても、関数を入力するだけで簡単に答えが得られます。そこで、細かな理屈は後のコラムにまとめることとして、まず、QUARTILE.EXC関数を使って四分位数と四分位範囲／四分位偏差を求めてみましょう。
サンプルファイルはこちらからダウンロードできます。［四分位範囲（EXC）］ワークシートを開いてみてください。データはあまり意味のなさそうな架空の値ですが、実は、筆者の高校時代の数学の実力テストを思い出す値です。私の点数は100点満点中たったの17点でした。が、しかし、周囲を見渡しても同じような点数の人たちばかり。あまりにも難しすぎたのです。しかし、その中でも満点近い点数を取る天才的な同級生もいました。このデータは、そういった外れ値や分布に偏りのある間隔尺度のデータ、あるいは、趣味や嗜好（しこう）、スポーツなどの成績をランキング（順位）で表した順序尺度のデータだと想像してください。
では、QUARTILE.EXC関数を入力して、第1四分位数から第3四分位数までを求めましょう（図3）。引数には以下の2つの値を指定します。
- データの範囲： セルA2〜A12に入力されている
- 四分位数の位置（何番目の四分位数を求めるか）： セルC3〜C5に入力されている値を使う
QUARTILE.EXC関数では、四分位数の位置として1未満の値や4以上の値は指定できません。というわけで、QUARTILE.EXC関数はセルD3〜D5に入力してください。四分位範囲の値と四分位偏差の計算は単なる四則演算なので簡単に求められます。それぞれ、セルD8とD9に入力することにしましょう。
なお、具体的な操作については動画で解説しているので、手順を丁寧に追いかけたい方はぜひご視聴ください（お約束のセリフですが、チャンネル登録・高評価もよろしくお願いします）。
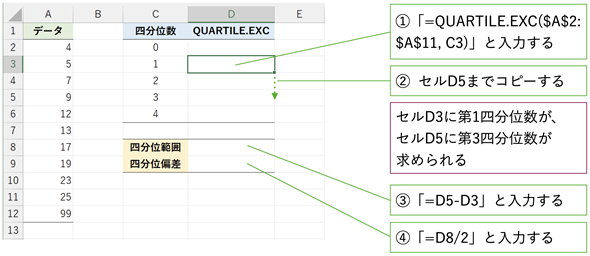図3 QUARTILE.EXC関数を使って四分位範囲／四分位偏差を求めるセルD3に「=QUARTILE.EXC($A$2:$A$12,C3)」と入力し、セルD5までコピーする。スピル機能を利用するなら、セルD3に「=QUARTILE.EXC(A2:A12,C3:C5)」と入力するだけでよい（Google スプレッドシートの場合は「=ARRAYFORMULA(QUARTILE.EXC(A2:A12,C3:C5))」となる）。セルD8には「=D5-D3」と入力し、セルD9には「=D8/2」と入力すればよい。
動画1 Excelで四分位範囲／四分位偏差を求める
数式を正しく入力できれば、四分位数として順に7、13、23という値が得られるはずです。セルD8の四分位範囲の値は16となり、セルD9の四分位偏差は8となります。答えはサンプルデータの［四分位範囲（EXCの答え）］というワークシートに含まれているので、そちらもご参照ください。
ところで、すでにお気づきかと思いますが、データの中には99という大きな値があります。しかし、四分位範囲や四分位偏差は、順位に基づく計算なので、極端な値の影響を受けにくくなっています。例えば、99という値が99999のようなきわめて大きな値であっても四分位範囲や四分位偏差は変わりません。
一方、前回取り上げた分散や標準偏差は極端な値の影響を強く受けます。試しに、空いているセルに「=STDEV.P(A2:A12)」と入力して標本標準偏差を求めてみてください。25.5という大きな値になることが分かります（平均値は21.2ですが、平均値を中心とした標準偏差の範囲内に99以外の値が全て収まってしまいます）。
四分位範囲／四分位偏差を求めてみよう（2） 〜 QUARTILE.INC関数を使う
次に、QUARTILE.INC関数を使って四分位数、四分位範囲の値、四分位偏差を求めてみましょう。［四分位範囲（INC）］ワークシートを開いてください。関数の形式は同じです。以下のような引数を指定します。
- データの範囲： セルA2〜A12に入力されている
- 四分位数の位置（何番目の四分位数を求めるか）： セルC2〜C6に入力されている値を使う
QUARTILE.INC関数では、引数に0を指定すると最小値が求められ、4を指定すると最大値が求められます。では、図4の流れに従って数式を入力していってください。
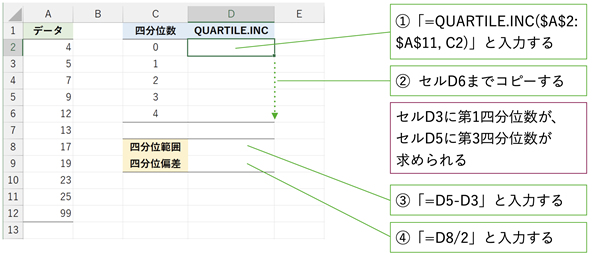図4 QUARTILE.INC関数を使って四分位範囲／四分位偏差を求めるセルD2に「=QUARTILE.INC($A$2:$A$12,C2)」と入力し、セルD6までコピーする。スピル機能を利用するなら、セルD2に「=QUARTILE.INC(A2:A12,C2:C6)」と入力するだけでよい（Googleスプレッドシートの場合は「=ARRAYFORMULA(QUARTILE.INC(A2:A12,C2:C6))」となる）。セルD8には「=D5-D3」と入力し、セルD9には「=D8/2」と入力すればよい。
数式を正しく入力できれば、四分位数が順に4、8、13、21、99となり、セルD8の四分位範囲の値が13、セルD9の四分位偏差が6.5となります。答えはサンプルデータの［四分位範囲（INCの答え）］というワークシートに含まれているので、そちらもご参照ください。
以上のように、四分位数は関数を入力するだけで求められます。といっても、実際にどういう計算が行われているのか分からないとちょっとモヤモヤした気になりますね。そこで、以下のコラムに詳細な計算方法を記しておきました。話がかなり細かくなるので、次に進みたい方はコラムを飛ばして、次の「四分位範囲を可視化するのに使われる箱ひげ図」や、その次の「名義尺度の散布度を求める 〜 平均情報量っていったい何？」に進んでいただいてもけっこうです。
コラム QUARTILE.EXC関数とQUARTILE.INC関数の計算方法
第1四分位数は小さい方から25％の位置にある値と考えられ、第3四分位数は小さい方から75％の位置にある値と考えられます。一般に、QUARTILE.EXC関数は0％と100％を含まない計算で、QUARTILE.INC関数は0％と100％を含む計算だと言われますが、意味がちょっと分かりにくいですね。そこで、それぞれの計算の考え方と四則演算のみでやってみた場合の手順を記します。以下の例は、サンプルファイルの［四分位範囲を手計算で］というワークシートに含まれています。データの件数をnとします。
QUARTILE.EXC関数の場合（第1四分位数の求め方）
QUARTILE.EXC関数では、k番目の値の位置をk/(n＋1)と考えます。全体をn＋1個と数えるので、25％の位置は(n＋1)×0.25番目となります。その位置にある値を第1四分位数とします。例えば、今回のサンプルデータではn＝11なので、(11＋1)×0.25＝3となり、3番目にある7という値が第1四分位数になります（図3に示した手順で実行した場合と同じ結果）。第3四分位数の場合は0.25の代わりに0.75を掛けて、位置を求めます。
しかし、25％の位置を表す値や75％の位置を表す値が整数にならないこともあります。例えば、最後の99という値を削除するとn＝10になるので、(10＋1)×0.25＝2.75となります。その場合は2番目にある5という値と次の3番目のある7という値の間隔、つまり7−5＝2を小数部分の0.75で比例配分します。したがって、5＋(7−5)×0.75＝6.5が第1四分位数となります。
これらの計算例は［四分位範囲を手計算で］というワークシートに含まれており、位置が整数になる場合も、そうならない場合にも対応した計算をしているので、ぜひ参照してみてください。以下の手順は、99という値を削除した場合の例です。
| 計算方法 | サンプルデータから99という値を取り除いた場合の例 | ||
|---|---|---|---|
| (n＋1)×25％の値を求める | (10＋1)×0.25 ＝ 2.75 | …… a とする | |
| aの整数部を求める | 2 | …… b とする | |
| aの小数部を求める | 0.75 | …… c とする | |
| bの位置にある値を求める | 2番目にあるのは5 | …… d とする | |
| bの次の位置にある値を求める | 3番目にあるのは7 | …… e とする | |
| d＋(e−d)×cを求める | 5＋(7−5)×0.75 ＝ 6.5 | …… Q1 | |
図1の中央値を除外して四分位数を求める方法と似ているが、25％の位置が整数にならない場合には(c)で求めた小数点以下の値を使って補間を行う。第3四分位数を求める場合は、(a)の値を求めるときに25％の代わりに75％を指定し、同様の方法で計算する。統計ソフトSPSSで標準的に使われている方法。
QUARTILE.INC関数の場合（第1四分位数の求め方）
QUARTILE.INC関数では、先頭を0として位置を表します。そのため、k番目の値の位置を(k−1)/(n−1)とします。全体をn−1個と数えるので、25％の位置は(n−1)×0.25＋1となります。1を足しているのは、先頭を元の並びに合わせて1番とするためです。求められた値が整数であれば、その位置にある値を第1四分位数とします。第3四分位数の場合は0.25の代わりに0.75を掛けて、位置を求めます。
25％や75％の位置が整数にならない場合はやはり小数部分で補間を行います。今回のサンプルデータではn＝11なので、(11−1)×0.25＋1＝3.5となり、3番目にある7という値と次の4番目にある9という値の間隔、つまり9−7＝2を0.5で比例配分し、7＋(9−7)×0.5＝8を第1四分位数とします（図4に示した手順で実行した場合と同じ結果）。
| 計算方法 | サンプルデータでの例 | ||
|---|---|---|---|
| (n−1)×25％＋1の値を求める | (11−1)×0.25＋1 ＝3.5 | …… aとする | |
| aの整数部を求める | 3 | …… bとする | |
| aの小数部を求める | 0.5 | …… cとする | |
| bの位置にある値を求める | 3番目にあるのは7 | …… dとする | |
| bの次の位置にある値を求める | 4番目にあるのは9 | …… eとする | |
| d＋(e−d)×cを求める | 7＋(9−7)×0.5 ＝ 8 | …… Q1 | |
図2の中央値を含めて四分位数を求める方法と似ているが、25％の位置が整数にならない場合にはcで求めた小数点以下の値を使って補間を行う。第3四分位数を求める場合は、aの値を求めるときに25％の代わりに75％を指定し、同様の方法で計算する。統計ソフトRで標準的に使われている方法。
統計ソフトのR（オープンソースで無料の統計解析向けプログラミング言語およびその開発実行環境）では、標準ではQUARTILE.INC関数と同じ計算が行われますが、全部で9種類の計算方法が選べるようになっています。Rではquartileではなく、quantileという関数を使います。quantile関数にtype=6を指定するとQUARTILE.EXC関数と同様の計算が行われます（ただし、最小値と最大値も返されます）。
> data <- c(4, 5, 7, 9, 12, 13, 17, 19, 23, 25, 99)
> quantile(data) # 何も指定しないとQUARTILE.INC関数と同様の結果
0% 25% 50% 75% 100%
4 8 13 21 99
> quantile(data, type=6) # type=6を指定するとQUARTILE.EXC関数と同様の結果
0% 25% 50% 75% 100%
4 7 13 23 99
四分位範囲を可視化するのに使われる箱ひげ図
四分位範囲を可視化し、分布を把握したり、外れ値を見つけたりするには箱ひげ図などが便利です。詳細な手順については、回を改めて、グラフを利用した可視化の方法を解説する予定なので、ここでは、箱ひげ図がどのようなものであるかということと、箱ひげ図の見方だけを簡単に紹介することにします。以下の図は、サンプルファイルの［箱ひげ図］ワークシートに含まれています（ただし、2023年6月の段階では、Googleスプレッドシートには箱ひげ図の機能がないので、グラフは表示されません）。
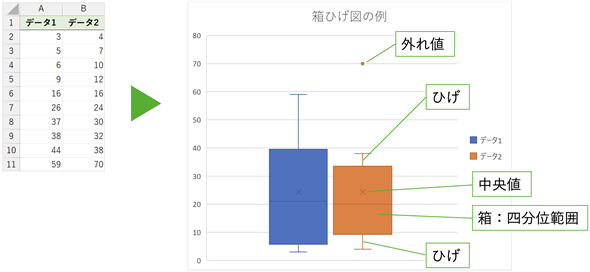図5 箱ひげ図とその見方特徴が分かりやすいようなデータを2つ用意して、箱ひげ図を作成した例。四分位範囲（IQR）が「箱」で描かれ、中央値の値がその中に「×」で示される。「箱」から上下に伸びている線が「ひげ」で、Excelの場合、「ひげ」の上限はQ3＋1.5×四分位範囲の値以下の最も近い値の位置となり、下限はQ1−1.5×IQR以上の最も近い値の位置となる。「ひげ」の上限と下限にある短い横線はキャップスラインとも呼ばれる。上限や下限からはみ出した値（外れ値）は○で示される。
左（データ1）の例は「箱」が全体の下の方にあるので、小さい値が比較的多くなっていることが分かります。右（データ2）の例は、極端に離れたところに大きな値がありますが、それ以外の部分のほぼ中央に「箱」があるので、外れ値以外の分布にはあまり偏りがないことが分かります。
図5は、Excelで箱ひげ図を作成した例ですが、特に何も指定しないと、四分位範囲を求めるためにQUARTILE.EXC関数で求めた四分位数が使われます。なお、平成29（2017）年告示の中学校学習指導要領（PDF）では、上限と下限の定義が上とは異なっており、最大値を「ひげ」の上限とし、最小値を「ひげ」の下限とした図になっていることに注意が必要です（外れ値があると「ひげ」が大きく伸びます）。
名義尺度の散布度を求める 〜 平均情報量っていったい何
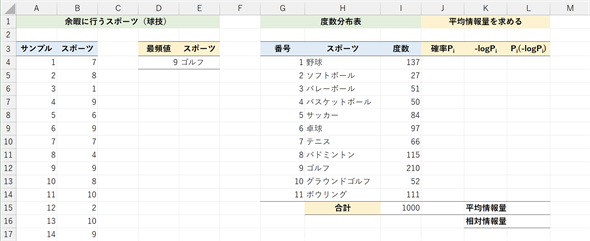
ここからは、名義尺度データのばらつきの度合いを表すために使われる平均情報量について見ていきます。まず、サンプルファイルをダウンロードして［平均情報量］ワークシートを開いてください。G列からI列に表示されているのは、第3回の記事で紹介した「余暇に行うスポーツ（球技）」の度数分布表です（図6）。
このようなデータで、ばらつきが大きいとか小さいということはどういうことでしょうか。例えば、1000人中1000人が「ゴルフ」と答えたとすると、答えが集中しているのでばらつきがないですね。一方、全てのスポーツの人数がほとんど同じであるとすると、答えはほぼバラバラです（この例では11種類のスポーツがあるので、それぞれの度数が1000/11＝91程度の場合）。つまりばらつきが大きくなります。そのようなばらつきの度合いを表すのが平均情報量です。名義尺度の散布度については、このようなイメージを持っていただくといいと思います。
といっても、これだけでは、なんとなく分かったような分からないような、という状態かもしれません。しかし、ここでも理屈は後回しにします。とにもかくにも、Excelを使って平均情報量を求めてみましょう。図7の数式に従って、手順通りに進めていけば計算ができます。
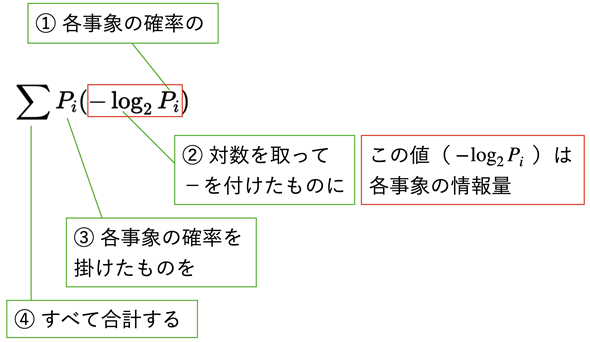図7 平均情報量を表す式「事象」とは、それぞれの「できごと」や「事柄」ということ。上の例では、「野球」や「ソフトボール」などの回答が何件あったかということ。数式の中の−log2Piは各事象の情報量を表す。それに確率を掛けたもの、つまりPi(−log2Pi)は、各事象の情報量を確率で重み付けした値。それらを合計すると平均情報量が求められる（後のコラムで解説するように、これは各事象の情報量を度数で重み付けして、全体の個数で割った値、つまり各事象の情報量の重み付け平均と同じ）。
まだ、情報量や平均情報量の意味がよく分からないかもしれませんが、手を動かして操作を追いかけてみると、少しずつその意味に気づくこともあるはずです。……が、やはり理屈が分からないとモヤモヤするという方は後掲の「コラム 情報量と平均情報量の定義」を先にお読みください。以降の操作については、動画で解説しているので、手順を丁寧に追いかけたい方はぜひご視聴ください。
動画2 Excelで平均情報量／相対情報量を求める
図7の式の中にあるPiはそれぞれの事象（できごと）が起こる確率です。例えば、このアンケートでは137人が「野球」と答えましたが、全体の人数が1000人なので、確率は137/1000＝0.137です。まず、このPiの値を求めるところからスタートしましょう（図8）。
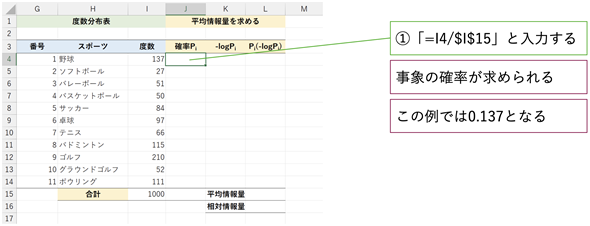図8 事象の確率を求めるセルJ4に「=I4/$I$15」と入力する。これで、「野球」の確率が求められる。数式を正しく入力すると、セルJ4に0.137と表示される。「I15」を絶対参照の「$I$15」にしているのは、後で数式をコピーするため。
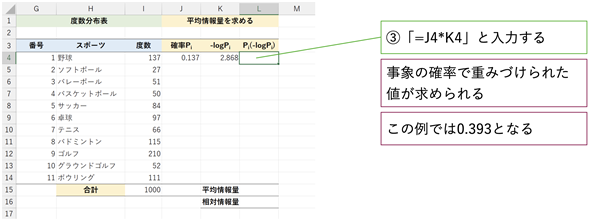
次に−log2Piを求めます（図9）。これは、各事象の情報量です。logは「対数」でしたね。logの後に小さく書かれた値は「底（てい）」と呼ばれます。「確かに、高校でそんなことを学んだような気がするけど、すっかり忘れてしまったよ」という方もご心配なく。対数の意味や計算方法を忘れていても、LOG関数を使えば値が求められます。
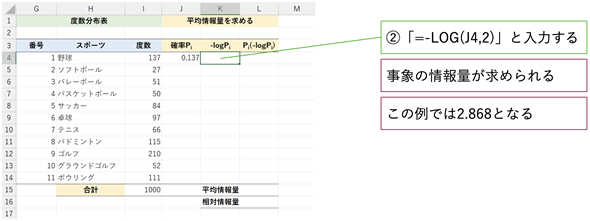図9 事象の情報量を求めるセルK4に「=-LOG(J4,2)」と入力する。これで、「野球」が137人であったときの情報量が求められる。LOG関数の2番目の引数には「底」の2を指定する。数式を正しく入力すると、セルK4に2.868と表示される。
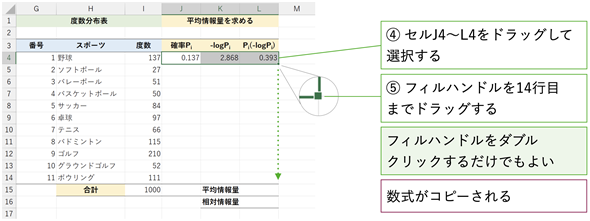
続いて、Pi(−log2Pi)を求めます（図10）。これは、情報量を確率で重み付けした値でしたね。図8で求めた値と図9で求めた値の積です。
ここまでで、「野球」について、情報量を確率で重み付けした値が求められました。他のスポーツについても同様の計算を行います。図8〜図10で入力した式（セルJ4〜L4）を全てのスポーツについて（14行目まで）コピーしましょう（図11）。
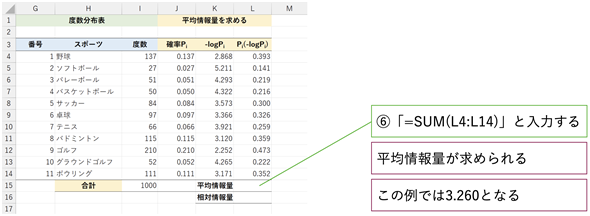
最後に、L列の値を合計すれば、平均情報量が求められます（図12）。
いかがでしょう。セルL15に3.260という値が表示されたら正解です。セルL16の相対情報量のお話はちょっと後回しにして、［平均情報量（答え）］というワークシートを開いて作成例を確認しておいてください。
スピル機能を使うなら、セルJ4に「=I4:I14/I15」、セルK4に「=-LOG(J4#,2)」、セルL4に「=J4#*K4#」と入力するだけで（コピーの操作は行わなくても）、セルJ4〜L14までの値が全て求められます。あとはセルL15で合計を求めるだけです。「J4#」などはスピル機能によって入力された範囲を表します（つまり「J4:J14」と同じ意味です）。
なお、Googleスプレッドシートの場合は、セルJ4に「=ARRAYFORMULA(I4:I14/I15)」、セルK4に「=ARRAYFORMULA(-LOG(J4:J14,2))」、セルL4に「=ARRAYFORMULA(J4:J14*K4:K14)」と入力します。
ちなみに、セルL15に、図8〜12の計算を全て組み合わせた「=SUM(-LOG(I4:I14/I15,2)*(I4:I14/I15))」という数式を入力するだけで、3.260という答えを得ることもできます（Googleスプレッドシートなら、「=ARRAYFORMULA(SUM(-LOG(I4:I14/I15,2)*(I4:I14/I15)))」）。
答えのワークシートには、全ての度数が同じ場合（平均情報量が最大になる場合）の例も含めてあります。平均情報量の最大値は、項目（カテゴリ）数をkとすると、それぞれの確率Piが全て1/kなので、
となります。この場合であれば、11個の項目があるのでlog211＝3.459となります。このように、平均情報量の最大値はカテゴリ数によって変わりますが、平均情報量をlog2kで割れば、最大値を1にそろえることができます。それが相対情報量です。［平均情報量］ワークシートに戻って試してみましょう。セルL16に「=L15/LOG(COUNT(I4:I14),2)」と入力すれば相対情報量が求められます。平均情報量が3.260だったので、相対情報量は3.260/3.459＝0.942となるはずです。相対情報量が1に近いことから、回答が比較的ばらけている（特定のスポーツのみに集中していない）ということが分かります。
なお、全ての人が「野球」と答えた場合は、他の項目がそもそも存在しないので、P＝1となり、平均情報量は0となります。
コラム 情報量と平均情報量の定義
平均情報量の定義を理解するに当たっては、まず、情報量がどのような値であるかを理解しておく必要があります。しかし、そもそも情報量が大きいとか小さいというのはどういうことでしょうか。
例えば「飛行機が空港に着陸した」というありふれた情報よりも、少し古いニュースですが「飛行機がハドソン川に不時着水した」という情報の方が、情報量が大きいような気がします。なんとなく感覚としては分かるのですが、数式として定義したいものです。
そこで、珍しいこと、つまり、起こる確率が小さいことが起こった（ということが分かった）場合に、情報量が大きくなるものとしましょう。そのためには、確率の逆数を求めるといいですね。確率Pが小さくなるほど、
は大きくなります。
ただし、
をそのまま情報量として使うのではなく、対数を取ったものを情報量とします。その理由は後述しますが、対数を取ると、
となります（底は2です。以降、底の表記は省略します）。これが情報量の定義で、単位はビット（bit）です。上の式の右辺は、以下に示す対数の公式を適用して求めたものです。
対数を取る理由は、掛け算を足し算として表したいからです。簡単な例で見てみましょう。正確な（1〜6のどの目も同じ確率で出る）サイコロを振ったとき、偶数の目が出たこと（Aとします）が分かった後に、それが6でなかった（つまり2か4であった）ことが分かった場合（Bとします）は、最初に考えた情報量の大きさ（確率の逆数）は以下のようになります。
このように情報を小出しにしても、最初から、2か4であることが分かったとしても、得られた情報量は同じです。
これらの値は、以下のような掛け算の関係になっています。
値を当てはめて確認してみましょう。
です。確かにA×B＝Cになっています。このように掛け算で表される式を、足し算で表すことを考えてみます。そのためには対数を取ればいいですね。
のとき、
です。これも対数に関係する公式そのままです。AやBの値をそのまま使うのではなく、対数を取った値を使うと、新たな情報が加えられたときに情報量を足し算として表すことができます。というわけで、対数を取った値を情報量として使うことにしたわけです。
話を元に戻して、次に平均情報量の定義です。平均情報量は情報量の期待値（度数で重みを付けた平均）です。つまり、それぞれの情報量に度数を掛けて、個数で割ったものです。それぞれの度数をFiとすると、
と表せます。確率は、度数を全体の個数で割ったものなので、
です。つまり、Fi ＝ nPiとなります。これを上の式に代入しましょう。
はい、これで平均情報量を求める式が得られました。なお、対数の意味や公式、情報量の定義、平均情報量については、「［AI・機械学習の数学］指数と対数（対数編）」でも解説しています。ぜひご参照ください。
今回は、集団のデータのばらつきの度合いを表す散布度について、順序尺度で使われる四分位範囲／四分位偏差と、名義尺度で使われる平均情報量／相対情報量の求め方や意味をそれぞれ解説しました。次回は、個々のサンプルの値が集団の中でどの位置にあるかということを考えます。単なる順位だけでなく、パーセント単位での順位を求めたり、偏差値を求めたりする方法を見ていきます。では、次回もお楽しみに！
関数リファレンス： この記事で取り上げた関数の形式
関数の使いこなし方については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
四分位数を求めるために使った関数
QUARTILE.EXC関数： 四分位数を求める（SPSSの標準的な方法）
形式
QUARTILE.EXC(値の並び, 四分位数)
引数
- 値の並び： 四分位数を求めたい元のデータを指定する。
- 四分位数： 1〜3を指定する。1なら第1四分位数、2なら第2四分位数（中央値）、3なら第3四分位数が求められる。
QUARTILE.INC関数： 四分位数を求める（SやRの標準的な方法）
形式
QUARTILE.INC(値の並び, 四分位数)
引数
- 値の並び： 四分位数を求めたい元のデータを指定する。
- 四分位数： 0〜4を指定する。0なら最小値、1なら第1四分位数、2なら第2四分位数（中央値）、3なら第3四分位数、4なら最大値が求められる。
対数を求めるために使った関数
LOG関数： 対数を求める
形式
LOG(数値, 底)
引数
- 数値： 対数を求めたい値（真数）を指定する。
- 底： 対数の底を指定する。省略すると10が指定されたものとみなされる。
Copyright© Digital Advantage Corp. All Rights Reserved.
ITmediaはアイティメディア株式会社の登録商標です。