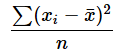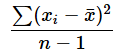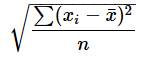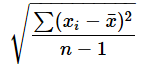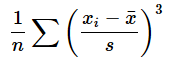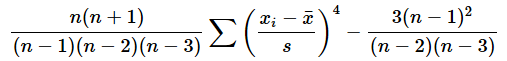［データ分析］分散／標準偏差 〜 給与の格差ってどれぐらい？：やさしいデータ分析

データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第4回。分布のばらつきの度合いを表す値として散布度を取り上げ、尺度や分布によって適切な散布度を利用する必要があることを説明します。今回は間隔尺度・比率尺度の散布度として使われる分散／標準偏差のお話です。

» 2023年06月15日 05時00分 公開
[羽山博，著]
「やさしいデータ分析」のインデックス

連載目次

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第4回です。前回は集団の中心的な位置を表す代表値について、尺度や分布によって平均値、中央値、最頻値を使い分けることについて説明しました。今回は、集団の性質を表す値として、分布のばらつきの度合いを表す散布度を取り上げます。

　やはり、尺度や分布により、分散／標準偏差、四分位範囲／四分位偏差、平均情報量／相対情報量を使い分ける必要があります。ただし、内容が少し多くなるので、今回は分散／標準偏差についてのみ見ていきます。四分位範囲や平均情報量などについては次回取り扱います。

連載：

『社会人1年生から学ぶ、やさしいデータ分析』

社会人1年生から学ぶ、やさしいデータ分析

　この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
　データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト（ExcelやGoogleスプレッドシート）を利用した作成例を紹介します。
　必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博 羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入（またもや金欠）。


サンプルファイルの利用について

　本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントがあれば使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントがあれば使える無料のGoogleスプレッドシート（Google Sheets）をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、.xlsxファイルをGoogleドライブにアップロードしてから開いた上で［ファイル］メニューの［Google スプレッドシートとして保存］を実行してください。

平均値だけで集団の性質を表すのは「雑」すぎる 〜 散布度も見よう

　平均値／中央値／最頻値といった代表値の意味や求め方については、前回、尺度ごとに詳しく見てきました。分布の違いによって、代表値の取り扱いには注意が必要であることも紹介しました。代表値はあくまで集団の中心的な位置を表すための値なので、集団の性質を表す値としてたった1つの代表値だけを使うのは、かなり「雑」だと言えます。

　例えば、令和元（2019）年の国民健康・栄養調査（厚生労働省）の結果（Excelファイルのダウンロード）では、20歳以上の男性の平均身長は167.7cm、20歳以上の女性の平均身長は154.3cmとなっていますが、身長は人それぞれです。平均値に近い人も多いでしょうが、読売ジャイアンツの秋広選手のように身長200cmの大柄な人もいれば、吉本新喜劇の池乃めだか師匠のように身長149cmの小柄な人もいます。167.7cmという代表値だけでは、集団の姿はよく分かりませんね。


AI博士

　ちなみに、CDC（Centers for Disease Control and Prevention）の調査によれば、調査時期は2015年〜2018年と、日本人のデータとは異なりますが、アメリカ人の男性の平均身長は69インチ（≈175.3cm）、女性の平均身長は63.5インチ（≈161.3cm）でした。アメリカ人の方が日本人よりも総じて身長が高いと言えます。代表値だけで集団の姿を浮き彫りにするのは難しいですが、集団同士を比較することはできます。


　代表値に頼り切るのではなく、分布を見ることによって、集団の姿がかなり分かってきます。分布を可視化するために使われるヒストグラムについても前回紹介しましたが、今回は、分布のばらつき具合を数値で表すことを考えてみたいと思います（今回も後でヒストグラムを掲載しますが、作成方法については回を改めて説明することとします。そのときのお楽しみということで……）。

　分布のばらつきの度合いを表す値は散布度と呼ばれ、やはり、尺度によって利用できる値が異なります。そこで、尺度と、その尺度で使われる散布度をまず見ておきましょう（表1）。前回のおさらいもかねて、代表値も合わせて示しておきました。

尺度 利用できる代表値 利用できる散布度 データの例
間隔尺度・比率尺度 平均値（算術平均） 分散／標準偏差 身長、体重、反応時間など
順序尺度 中央値 四分位範囲／四分位偏差 ランキングの順位、五段階評価など
名義尺度 最頻値 平均情報量／相対情報量 製品名、好きなスポーツの種類など
表1　尺度と散布度
間隔尺度や比率尺度なら分散または標準偏差、順序尺度なら四分位範囲（または四分位偏差）、名義尺度なら平均情報量（または相対情報量）を散布度として使う。以下の説明にあるように、上の方に記した尺度では、下の方に記した散布度も使える。

　基本的に表1の上の方に記した尺度では、下の方に記した散布度も使えます。例えば、間隔尺度や比率尺度では分散や標準偏差を使いますが、四分位範囲や四分位偏差を使うこともできます。特に、外れ値や分布に偏りがある場合には、そういったデータの影響を受けにくいというメリットがあります。しかし、その逆はできません。例えば、名義尺度の散布度として分散／標準偏差や四分位範囲などを使うことはできません。ただし、順序尺度の場合、本来は四分位範囲や四分位偏差を使いますが、五段階評価などで分布にあまり偏りがない場合は、便宜的に間隔尺度と見なして分散や標準偏差を使うこともあります。

間隔尺度の散布度を求める 〜 まずは分散から

　理屈は後回しにし、前回利用した「勤め先収入」に関連するデータを使って計算してみましょう。勤め先収入のデータは間隔尺度のデータなので、分散や標準偏差が使えます。そこで、まずは分散をExcelで求めることにします（標準偏差については後で見ます）。

　サンプルファイルはこちらからダウンロードできます。今回はデータを2種類用意してあります。［勤め先収入(1)］ワークシート（前回利用したもの）と、［勤め先収入(2)］ワークシート（今回追加したもの）です。いずれも平均は49.2ですが、ばらつきが異なるものとなっています。

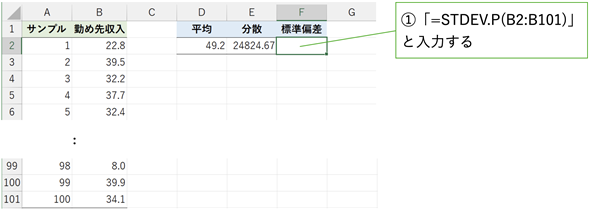
　ではやってみましょう。分散はVAR.P関数で求められます。引数にはデータの範囲を指定するだけです。セルB2〜セルB101に入力されている勤め先収入のデータを基に、分散をセルE2に求めてみてください（図1）。それぞれのワークシートで分散の値を求め、比較してみましょう。具体的な操作については、標準偏差の求め方と合わせて動画で解説しているので、手順を丁寧に追いかけたい方はぜひご視聴ください（お約束のセリフですが、チャンネル登録・高評価もよろしくお願いします）。

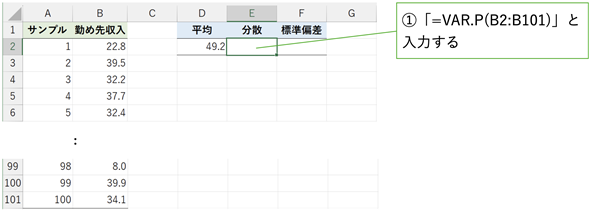勤め先収入の分散 図1　勤め先収入の分散を求めてみる
［勤め先収入(1)」というワークシートを開き、セルE2に「=VAR.P(B2:B101)」と入力して分散を求めよう。［勤め先収入(2)」についても同様。これらのデータは、総務省統計局の家計調査の統計表（Excelファイルのダウンロード）に掲載された2022年の調査結果と平均値が同じになるようにしてある（ただし、分散や標準偏差は実際の値とは同じではない）。

動画1　Excelで分散／標準偏差を求める


　答えは簡単、いずれのワークシートでもセルE2に「=VAR.P(B2:B101)」と入力するだけです。［勤め先収入(1)］のデータでは、分散が24824.67となり、［勤め先収入(2)］のデータでは283.88となるはずです。このことから、［勤め先収入(1)］のばらつきの方が大きいことが分かります（が、後述するように、ちょっとした落とし穴もあります）。答えはサンプルデータの［勤め先収入(1の答え)］と［勤め先収入(2の答え)］というワークシートに含まれているので、そちらもご参照ください。

　分布の違いが可視化できるように、ヒストグラムも掲載しておきます（図2）。

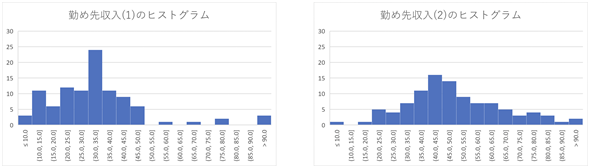勤め先収入の分散 図2　勤め先収入のヒストグラム
［勤め先収入(1)］の分散の方が大きいのだが、ヒストグラムを見ると、平均値よりかなり小さい位置に値が集中している。分散が大きいのに、ばらつきがそれほど大きくないように見えるのは、1600などの極端な外れ値が含まれており、それが「90より大」という階級にまとめられているため。［勤め先収入(2)］は、平均値よりわずかに小さい位置に値が集中しており、なだらかに裾野が広がるような分布になっている。

　［勤め先収入(1)］の分散の方が大きいのに、値が集中して見え、［勤め先収入(2)］の分散の方が小さいのに、広い範囲に値が散らばっているように見えます。これはいったいなぜでしょうか。すでに察しの付いた方もおられると思いますが、その犯人は「外れ値」です。前回もお話したように［勤め先収入(1)］のデータには、外れ値と考えられる値が含まれています。

　分散も極端な値があるとそれに引きずられることに注意が必要です。例えば、極端な値を上位から3つ（1600、200、124）を除外して分散を求めてみると171.32となり、［勤め先収入(2)］よりもばらつきが小さくなります。つまり、比較的小さな階級に値が集中していることが分かります。分散が大きくても、ばらついていないこともあるわけです。これも外れ値による落とし穴ですね。

コラム　外れ値を検出するには

　発展的なお話になりますが、外れ値の検出には、スミルノフ・グラブス検定などが使えます。［勤め先収入(1)］の例では、1％水準で検定を行ったときに1600、200、124という3つの値が外れ値と見なされました。統計ソフトとしてよく使われているR（オープンソースで無料の統計解析向けプログラミング言語およびその開発実行環境）を利用すると、以下のように求められます。

> install.packages("outliers")  # outliersパッケージをインストール
> library(outliers)  # outliersパッケージを読み込む
> data <- c(22.8, 39.5, 32.2, ... 39.9, 34.1)  # 途中を省略してあるが全てのデータを指定する
> grubbs.test(data)  # スミルノフ・グラブス検定を行う（大きい方から1つ検出）

    Grubbs test for one outlier

data:  data
G = 9.793359, U = 0.021428, p-value < 2.2e-16
alternative hypothesis: highest value 1600 is an outlier

# 以下、外れ値と判断されたデータを除外して同じことを繰り返し行う
# 1％水準（p-valueが0.01以下）の場合、1600、200、124が外れ値と見なされる


R言語のインタラクティブコンソールでスミルノフ・グラブス検定を行っている例

　なお、これらの値をExcelで求めた例もサンプルファイルの［外れ値の検出］ワークシートに含めてあります。あくまで参考としてですが、サンプルファイル中には手順も記してあります。


　ここで求めた24824.67や283.88などの分散の値を比較すれば、分布のばらつきの違いが分かります。しかし、値そのものが何を表しているのかが分からないですね。

　分散や標準偏差の計算方法は後で説明しますが、分散の計算では途中で元の値を2乗するので、元の値の単位とは規模が異なる値になってしまいます。そこで、次に標準偏差の登場です。標準偏差は分散の√を取った値なので、元の値と同じ単位になります。

間隔尺度の散布度を求める 〜 標準偏差も求めよう

　では、標準偏差を求めてみましょう。上で使った［勤め先収入(1)］と［勤め先収入(2)］のデータを使います。すでに分散を求めたのでその√を取っても構いませんが、ここでは標準偏差を求めるためのSTDEV.P関数を使います。やはり、引数にはデータの範囲を指定するだけです。セルB2〜セルB101に入力されている勤め先収入のデータを基に、標準偏差をセルF2に求めてみてください（図3）。それぞれのワークシートで標準偏差の値を求め、比較してみましょう。

勤め先収入の標準偏差 図3　勤め先収入の標準偏差を求めてみる
［勤め先収入(1)］というワークシートを開き、セルF2に「=STDEV.P(B2:B101)」と入力して標準偏差を求めよう。［勤め先収入(2)］についても同様。

　いずれのワークシートでもセルF2に「=STDEV.P(B2:B101)」と入力するだけです。［勤め先収入(1)］のデータでは、標準偏差が157.56（万円）となり、［勤め先収入(2)］データでは16.85（万円）となるはずです。当然のことながら、標準偏差からも［勤め先収入(1)］のばらつきの方が大きいことが分かります。加えて、［勤め先収入(1)］のばらつきが異常に大きいのではないかということも分かりますね。

　分布のばらつきの度合いを表すのに、実感の湧きにくい分散なんて使わなくても、標準偏差だけで十分じゃないの、と思われる方もおられるかもしれません。しかし、統計のさまざまな計算の中で分散の値はよく使われます。分散が使われるのは、わざわざ√を求めず、分散の値のままにしておいた方が計算上便利なことも多いからです。

「ばらつきの度合い」とは平均値からどれぐらい離れているかということ

　分散や標準偏差は、理屈を知らなくても、Excelの関数を使えば簡単に求めることができます。しかし、分布のばらつきの度合いを表す値として、なぜ分散や標準偏差が使われるのかを理解しておくことは重要です。そこで、VAR.P関数やSTDEV.P関数を使わず、四則演算だけで分散や標準偏差を求めてみましょう。そうすれば、分散や標準偏差の意味がよく分かります。仕組みさえ分かればいいので、簡単なデータでやってみます。

　サンプルファイルの［分散を手計算で］ワークシートを開いてください。手順は以下の通りです。ここでは分散を求める手順を見ていくことにします。

  1. 各データと平均値の差を求めて2乗する
  2. それらを全て足す
  3. データの個数で割る

　では、図4の流れに従って、数式を入力していってください。

分散を手計算で求める 図4　分散を手計算で求めてみる
手順通りに数式を入力すれば、分散が求められる。計算の意味については後述。なお、このデータは気象庁の「観測開始から毎月の値」から、2013年〜2022年の年間降水量を取り出し、月平均の値にしたもの。単位はmm。

　正しく数式が入力できたら、セルG2に238.46という値が表示されます。この値はVAR.P関数を使って求められる値と一致します。空いているセルに「=VAR.P(B2:B11)」と入力して確認しておいてください。答えはサンプルファイルの［分数を手計算で（答え）］というワークシートに含まれているので、そちらも参照してみてください。


AI博士

　Microsoft 365（Excel 2019以降）であれば、スピル機能を利用して、セルC2に「=B2:B11-B12」と入力し、セルD2に「=C2:C11^2」と入力すると、コピー操作をしなくても、セルC2〜D11の数式が全て入力できます。

　Google スプレッドシートの場合は、配列数式を作成するためのARRAYFORMULA関数を使って、セルC2に「=ARRAYFORMULA(B2:B11-B12)」と入力し、セルD2に「=ARRAYFORMULA(C2:C11^2)」と入力します。ただし、サンプルファイルをGoogleドライブにアップロードすると、［分数を手計算で（答え）］ワークシートのセルD2には「=ARRAY_CONSTRAIN(ARRAYFORMULA(C2:C11^2), 10, 1)」という式が表示されます。このARRAY_CONSTRAIN関数は配列の一部だけを表示したいときに使う関数です。この例では、結果を全て求めたいので、特にARRAY_CONSTRAIN関数を使う必要はありません。今後、この連載では必要のない限り「=ARRAY_CONSTRAIN(ARRAYFORMULA(C2:C11^2), 10, 1)」のように入力されていても、配列数式を表す部分、つまり「=ARRAYFORMULA(C2:C11^2)」だけを掲載することにします。


　では、計算の意味を考えてみましょう。「各データと平均値の差」は、それぞれのデータが平均からどれだけ離れているかということです。それらを合計すれば、各データと平均値がどれだけ離れているかの合計が求められます。しかし、「各データと平均値の差」は正になることも負になることもあるので、単純に合計すると正と負が相殺されてしまいます。そこで、合計を求めるに当たって、絶対値にしておきます。そのために、「各データと平均値の差」を2乗しています。そうすれば、全てが正の値になりますね（負の値の2乗は正の値になります。後で√を求めれば絶対値にできます）。

　「各データと平均値の差」を2乗した値の合計を求め、データの個数で割ると、各データと平均値がどれだけ離れているかの平均が求められます。つまり、分散とは、各データが平均値から平均的にどれだけ離れているかという値であるということです。標準偏差は分散の√を取って、2乗する前の単位に戻した値であることも分かります。

分散や標準偏差をイメージで理解しよう

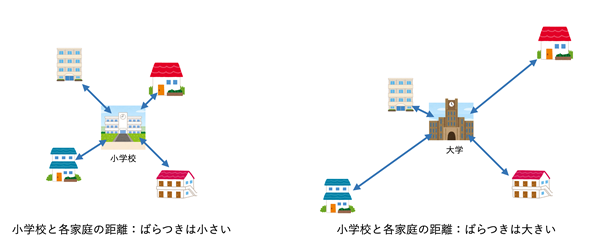
　うーん、まだ実感が湧かないな、という方は、以下のようなたとえ話でイメージをつかんでもらうといいのではないかと思います。一般に、公立の小学校には地域の子供たちが通っているので、小学校と各家庭との距離のばらつきは小さいですね。それらの距離（を2乗したもの）の平均が分散です。一方、大学には、近くの寮から通っている学生もいますが、遠距離から新幹線通学している学生もいます。つまり、大学と各家庭や寮などとの距離のばらつきの度合いは大きくなります。分散が大きくなることも納得できると思います。

分散のイメージ 図5　分散のイメージ
学校と各家庭との距離（の2乗）の平均が、ばらつきの度合いを表す。公立の小学校であれば、比較的ばらつきが小さい。大学であれば、ばらつきは大きくなる。

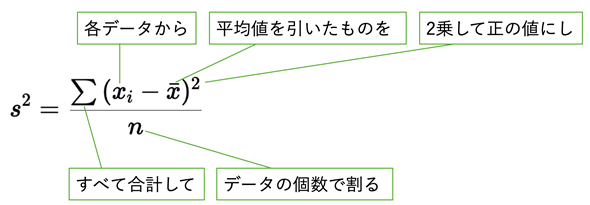
分散や標準偏差を数式できちんと理解しよう

　さらに、分散を求めるための数式も見ておきましょう。標準偏差をsとし、分散はs2とすれば、図6のような式になります。数式が苦手な方はスルーしてもらっても構いませんが、毎度毎度「各データから平均値を引いたものを2乗し、それらの合計を求めて、データの個数で割る」と表現するのは面倒ですよね。数式はそういったことをできるだけ簡潔に表したものです。むしろ、面倒な計算手順を簡単に書けるだけでなく、一目見ただけでも意味が分かる便利な表し方なのだと考えてもらうと、数式がぐっと身近に感じられるのではないかと思います。

分散を求めるための式 図6　分散を求めるための式
$x_i$は各データ、$\bar{x}$は平均値、$n$はデータの個数です。$\sum$は合計するという意味なので、この式は、各データから平均値を引いたものを2乗し、それらの合計を求めて、データの個数で割るということになる。

コラム　その「ばらつき」って、どの「ばらつき」?! 〜 2種類の分散と標準偏差

　Excelの関数について調べたことのある方には、分散を求める関数にはVAR.P関数とVAR.S関数があり、標準偏差を求める関数にはSTDEV.P関数とSTDEV.S関数があることをご存じの方も多いと思います。これらの関数で求められる値や計算方法は表2のようにまとめられます。が、いったい、どう違うのでしょうか。

標本分散／標本標準偏差と不偏分散／不偏標準偏差の違いを説明する表 表2　標本分散／標本標準偏差と不偏分散／不偏標準偏差の違い
標本分散とは、取り出した値（標本やサンプルと呼ばれる）そのものの分散を表す。一方の不偏分散は取り出した標本を基に、母集団（全体）の分散を推定した値。分母がn−1になっているので、標本分散よりも不偏分散の方が少し値が大きくなる。標準偏差についても同じ考え方。

　上の表の説明にもあるのように、標本分散は標本そのものの分散を表す値です。一方、不偏分散は標本を基に母集団の分散を推定した値です（図7）。

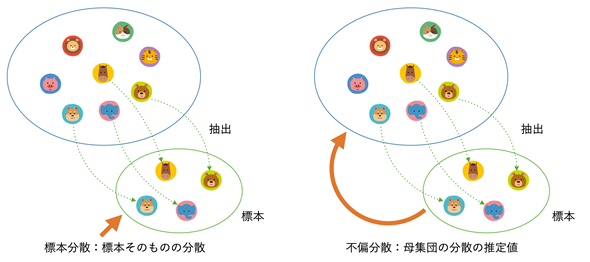標本分散と不偏分散 図7　標本分差と不偏分散の違い
標本分散は標本そのものの分散。全数調査のように、標本が母集団全体である場合も標本分散を求めることになる。不偏分散は母集団から抽出した標本を基に、母集団の分散を推定した値。

　勤め先収入の例には100件の標本があり、今回は標本そのものの分散を求めるためにVAR.P関数を使って標本分散を求めました。しかし、それらの値を基に、勤め先がある人全体の収入の分散を推定したい場合には不偏分散を使います。その場合は、VAR.S関数を使います。引数の指定方法は全く同じです。標本標準偏差と不偏標準偏差の違いも、分散の場合と同じ考え方です。

　不偏分散や不偏標準偏差の場合、分母がnではなくn−1になっているのには深い理由があるのですが、取りあえず、n−1で割った方が適切な推定値が得られるという理解で実用上困ることはありません（が、証明について興味のある方は、「高校数学の美しい物語　不偏標本分散の意味とn-1で割ることの証明」などをご参照ください）。

　なお、文献によっては、標本分散のことを単に分散と呼び、不偏分散のことを標本分散と呼んでいるものもあります。用語が紛らわしいですが、どのようなデータを対象としてどのような分析を行っているのかが分かっていれば、どちらの意味で使っているのかは文脈から分かると思います。


AI博士

　Excelの中でも、関数では標本分散／不偏分散という用語が使われていますが、集計機能やピボットテーブルでは、分散／標本分散という用語が使われており、統一されていません。



コラム　歪度と尖度で分布の形を知る

　ヒストグラムを見れば分布の形が可視化できますが、値が集まっているように見えるとか、なんとなくばらけているといった感覚でしか捉えられません。イメージをつかむことも大切ですが、分布の形を何らかの数値で表すことはできないでしょうか。

　実は、歪度（わいど）と呼ばれる値により、分布の歪み（ゆがみ）を知ることができます。

　また、尖度（せんど）と呼ばれる値により、値が集中しているかどうかを知ることができます（図8）。

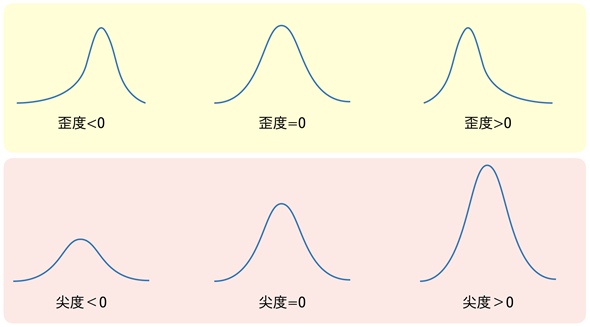分布の形と歪度／尖度 図8　分布の形と歪度／尖度
［山が右側（大きい値の方）にあり、左側（小さい値の方）に裾野が広がった分布の場合、歪度が負になる。逆に山が左側にあり、右側に裾野が広がった分布の場合、歪度は正になる。山が尖っている（値が集中している）場合には、尖度が大きくなり、山がなだらかな場合には、尖度は小さくなる。なお、尖度の定義によっては、図の下に示した値が順に「尖度＜3」「尖度＝3」「尖度＞3」となっていることもある。

　歪度はSKEW関数やSKEW.P関数で求められ、尖度はKURT関数で求められます。いずれも引数には元のデータを指定するだけです。［勤め先収入(1)］ワークシートと［勤め先収入(2)］ワークシートのセルD5とE5に「=SKEW(B2:B101)」「=KURT(B2:B101)」と入力して値を比較してみてください。表2のような値が得られるはずです。

尺度 ［勤め先収入(1)］ ［勤め先収入(2)］ 備考
歪度 9.69 0.42 ［勤め先収入(1)］の方が左に山のある分布
尖度 95.64 -0.01 ［勤め先収入(1)］の方が山が高い分布
表3　歪度と尖度
それぞれの値と図8のパターンとを照らし合わせて見れば、図2のヒストグラムのイメージと一致していることが分かる。なお、歪度と尖度を「この記事で取り上げた関数の形式」に記した定義通りに、四則演算のみで求めた例をサンプルファイルとして用意してあるので、興味があれば参照されたい。


　今回は、集団のデータのばらつきを表す散布度について、分布や尺度による取り扱いの違いを見た後、間隔尺度や比率尺度の散布度として使われる分散／標準偏差の求め方や意味を解説しました。次回は、引き続き、順序尺度で使われる四分位範囲／四分位偏差と名義尺度で使われる平均情報量／相対情報量について見ていきます。では、次回もお楽しみに！

関数リファレンス： この記事で取り上げた関数の形式

　関数の使いこなし方については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます

分散や標準偏差を求めるために使った関数

VAR.P関数： 標本分散を求める

形式

VAR.P(数値1, 数値2, ... , 数値255)

引数

  • 数値： 標本分散を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

以下の式に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数。

VAR.S関数： 不偏分散を求める

形式

VAR.S(数値1, 数値2, ... , 数値255)

引数

  • 数値： 不偏分散を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

以下の式に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数。

STDEV.P関数： 標本標準偏差を求める

形式

STDEV.P(数値1, 数値2, ... , 数値255)

引数

  • 数値： 標本標準偏差を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

以下の式に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数。

STDEV.S関数： 不偏標準偏差を求める

形式

STDEV.S(数値1, 数値2, ... , 数値255)

引数

  • 数値： 不偏標準偏差を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

以下の式に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数。

分布の形を知るために使った関数

SKEW関数： 歪度を求める（SPSS方式）

形式

SKEW(数値1, 数値2, ... , 数値255)

引数

  • 数値： 歪度を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

統計ソフトとしてよく使われているSPSSでの計算方法（以下の式）に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数、\(s\)は不偏標準偏差。

SKEW.P関数： 歪度を求める

形式

SKEW.P(数値1, 数値2, ... , 数値255)

引数

  • 数値： 歪度を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

一般的に使われる以下の式に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数、\(s\)は不偏標準偏差。

KURT関数： 尖度を求める（SPSS方式）

形式

KURT(数値1, 数値2, ... , 数値255)

引数

  • 数値： 歪度を求めたい数値やセル範囲を指定する。引数は255個まで指定できる。

備考

統計ソフトとしてよく使われているSPSSでの計算方法（以下の式）に基づいて求められる。\(x_i\)は各データ、\(\bar{x}\)は平均値、\(n\)はデータの個数、\(s\)は不偏標準偏差。

Googleスプレッドシートで配列数式を利用するための関数

ARRAYFORMULA関数： 数式を配列数式にする

形式

ARRAYFORMULA(数式)

引数

  • 数式： 配列数式にしたい式を指定する。

ARRAY_CONSTRAIN関数： 配列の一部を返す

形式

ARRAY_CONSTRAIN(配列, 行数, 列数)

引数

  • 配列： 値の並びやセル範囲、配列数式などを指定する。
  • 行数： 配列から取り出す行数を指定する。
  • 列数： 配列から取り出す列数を指定する。

「やさしいデータ分析」のインデックス

「やさしいデータ分析」

Copyright© Digital Advantage Corp. All Rights Reserved.

＠IT

@ITについて

RSSについて

アイティメディアIDについて

メールマガジン登録

＠ITのメールマガジンは、 もちろん、すべて無料です。ぜひメールマガジンをご購読ください。