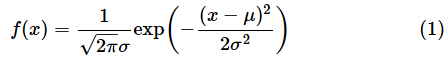［データ分析］順位と偏差値 〜 私の成績順位はどのあたり？：やさしいデータ分析

データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第6回。集団の中での位置をパーセント単位で求めたり、偏差値を求めたりする方法と、その考え方を説明します。偏差値は大学や高校のランク付けによく使われていますが、序列を付けるためのものではなく、異なる分布の集団の間でも位置が比較できるとても便利な値です。

[羽山博，著]

連載目次

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第6回です。これまでは、集団のばらつきの度合いを表す散布度について見てきました。具体的には、前々回は間隔尺度や比率尺度で使われる分散／標準偏差を、前回は、順序尺度で使われる四分位範囲／四分位偏差と、名義尺度で使われる平均情報量／相対情報量を紹介しました。今回は、集団そのものの特徴から少し視点を変えて、集団の中にある個々の値に注目していきます。個々の値が集団の中でどの位置にあるのかをパーセント単位で求める方法や、異なる分布の集団の間で位置を比較できる偏差値について見ていきます。

連載：

『社会人1年生から学ぶ、やさしいデータ分析』

　この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
　データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト（ExcelやGoogleスプレッドシート）を利用した作成例を紹介します。
　必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入（またもや金欠）。

サンプルファイルの利用について

　本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントがあれば使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントがあれば使える無料のGoogleスプレッドシート（Google Sheets）をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、.xlsxファイルをGoogleドライブにアップロードしてから開いた上で［ファイル］メニューの［Google スプレッドシートとして保存］を実行してください。

まずは単純に順位を求めてみよう

　集団の中での順位を求める方法については、誰もが直感的に理解していることと思います。そこで、以下（表1）のような成績のデータに順位を付けてみてください。まずは手作業でやってみましょう。作業しやすいように、データは降順（大きい値から小さい値への順）に並べ替えてあります。

成績	95	90	82	81	78	69	67	54	54	35	24	12
順位
表1　成績のデータに順位を付けてみましょう（［順位］欄に番号を振る）

　皆さんはどのように順位を付けたでしょうか。以下（表2）のような付け方をした人が多いと思います。

成績	95	90	82	81	78	69	67	54	54	35	24	12
順位	1	2	3	4	5	6	7	8	8	10	11	12
表2　成績のデータに順位を付けた例（1）

　54点の人が2人いるので、同じ8位という順位を与えました。その次は10位としたわけです。つまり、同じ点数の人が複数いる場合には、上位の順位を与えて、後ろは欠番とするわけですね。ExcelのRANK.EQ関数で順位を求めるとこれと同じ結果になります。

　別の考え方もあります。8位と9位が同じ得点だったので、上位と下位の平均の順位、つまり(8＋9)÷2＝8.5を2人に与えるという考え方です。その場合は、以下（表3）のような順位になります。

成績	95	90	82	81	78	69	67	54	54	35	24	12
順位	1	2	3	4	5	6	7	8.5	8.5	10	11	12
表3　成績のデータに順位を付けた例（3）

　ExcelのRANK.AVG関数では、このような順位の求め方になります。

　では、さっそくExcelを使って……と行きたいところですが、それぞれの関数を使ったときにどのような結果になるかを予想してからやることにしましょう。上とはちょっと違った例です（表4）。同じ順位が3人いることにも注意してください。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

成績	95	90	82	78	78	69	67	54	54	54	24	12
RANK.EQでの順位	1	2	3	4	4	6	7	8	8	8	11	12
RANK.AVGでの順位	1	2	3	4.5	4.5	6	7	9	9	9	11	12
表4　成績のデータに順位を付けてください（表1〜3と成績の内容が異なることに注意）

　予想は当たっていたでしょうか。54点が3人いますが、RANK.EQ関数の場合は上位の順位を与えるので、いずれも8位となります。その次が11位ですね。RANK.AVG関数の場合は、8位、9位、10位の上位と下位の平均なので、全て9位を与えます。その次が11位になるのは同じです。

　では、Excelで試してみましょう。サンプルファイル（06a.xlsx）をこちらからダウンロードし、［順位を求める］ワークシートを開いて試してみてください。以下で説明する操作については動画でも解説しているので、手順を丁寧に追いかけたい方はぜひご視聴ください。

動画1　Excelで順位を求める

　RANK.EQ関数でも、RANK.AVG関数でも、第1引数には対象となる値を指定し、第2引数には、全ての値を指定します。第3引数には降順での順位か昇順での順位かを指定します。降順の場合は0を指定するか省略し、昇順の場合は0以外の値を指定します。降順の場合は値が大きいほど上位になり、昇順の場合は値が小さいほど上位になります。なお、値は並べ替えられていなくても構いません。

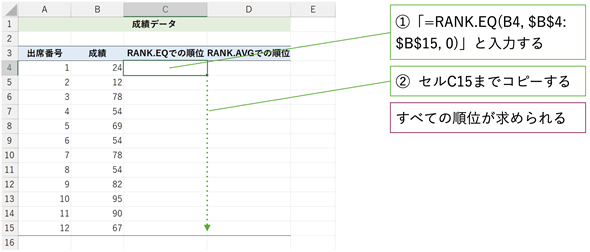
　図1にRANK.EQ関数を入力する手順を示します。手順に従って操作してみてください。

図1　RANK.EQ関数を使って順位を求める
［順位を求める］ワークシートを開き、セルC4に「=RANK.EQ(B4,$B$4:$B$15,0)」と入力して順位を求めよう。

　セルC4に「=RANK.EQ(B4,$B$4:$B$15,0)」と入力し、セルC15までコピーしてください。スピル機能を使うならセルC4に「=RANK.EQ(B4:B15,B4:B15,0)」と入力するだけで全ての順位が求められます。Googleスプレッドシートで配列数式を使うなら、セルC4に「=ARRAYFORMULA(RANK.EQ(B4:B15,B4:B15,0))」と入力すれば同じ結果が得られます。

　RANK.AVG関数については、関数名が異なるだけで、引数の指定は全く同じです。セルD4に「=RANK.AVG(B4,$B$4:$B$15,0)」と入力して、セルD15までコピーすると、図2のような結果が得られます。スピル機能を使うなら「=RANK.AVG(B4:B15,B4:B15,0)」となり、Googleスプレッドシートで配列数式を使うなら、「=ARRAYFORMULA(RANK.EQ(B4:B15,B4:B15,0))」となります。

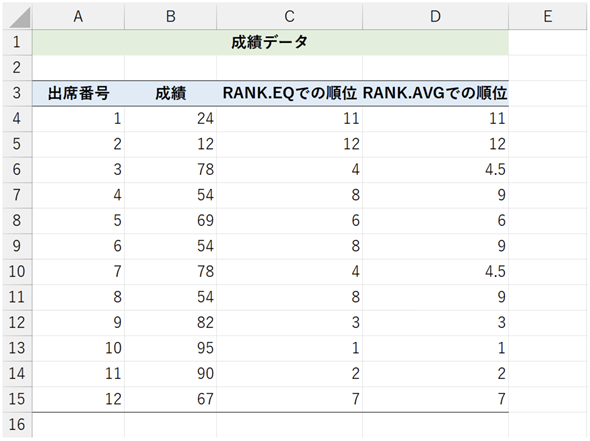図2　RANK.EQ関数とRANK.AVG関数で求めた順位
成績順に並べ替えられていないので少し分かりづらいが、予想した順位と同じ結果が得られた。RANK.EQ関数では、4位が2名、8位が3名となり、RANK.AVG関数では、4.5位が2名、9位が3名となる。作成例は［順位を求める（答え）］ワークシートに含まれている。

　図2の結果を見ると、実際に試験を受けてある点数を取った人が何位であるかは分かりますが、例えば、その試験で80点を取ったとすればどの辺りの位置にいるかは分かりません。実は、RANK.EQ関数やRANK.AVG関数では、順位を求める対象となる値（この場合なら80点）がデータの中に存在しないとエラーになってしまいます。そこで、次に、データの中に存在しない値を指定しても順位が求められる方法を見ていくことにします。そのためには、値が全体の何パーセントの位置にあるかを求めます。

　図1や図2のデータは出席番号順に並んでいるので、自分の成績や順位が一目で見つけられます。しかし、データを分析する場合には、成績の降順または昇順に並んでいた方が便利です。並べ替えもデータ分析のために使われる基本的な手法なので、番外編として並べ替えの方法も解説する予定です。

80点を取ったら第何位？

　順位を基にして、ある値が全体の何パーセントの位置にあるかを求めるには、PERCENTRANK.EXC関数またはPERCENTRANK.INC関数が使えます。

　これまでに見てきたデータを例に、80点を取ると全体の何パーセントの位置にいるかを求めてみましょう。サンプルファイル（06b.xlsx）をこちらからダウンロードし、［順位（PERCENTRANK.EXC）］ワークシートを開いて以下の操作を行いましょう。これについても、操作は動画でも解説しています。手順を丁寧に追いかけたい方はぜひご視聴ください。

動画2　Excelでパーセント単位での順位を求める

　図3にPERCENTRANK.EXC関数を入力する手順を示します。

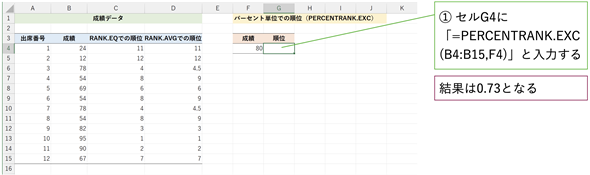図3　パーセント単位での順位を求める（PERCENTRANK.EXC関数）
［順位（PERCENTRANK.EXC）］ワークシートを開き、セルG4に「=PERCENTRANK.EXC(B4:B15,F4)」と入力して順位を求めよう。
作成例は［順位（PERCENTRANK.EXC答え）］ワークシートを参照。データの最小値より小さい値や、データの最大値より大きい値を指定するとエラーになることに注意。

　PERCENTRANK.EXC関数の引数にはデータの範囲と順位を求めたい値を指定します。関数の実行結果は0.730、つまり73％となるはずです。ただし、Googleスプレッドシートでは、有効桁数の取り扱いが異なるので0.731と表示されます（Excelでは切り捨て、Googleスプレッドシートでは四捨五入が行われているようです）。

　PERCENTRANK.INC関数の場合も、関数名が違うだけで、引数の指定方法は同じです。［順位（PERCENTRANK.INC）］ワークシートを開いて、セルG4に「=PERCENTRANK.INC(B4:B15,F4)」と入力してみてください。結果は0.772、つまり77.2％となります。作成例は［順位（PERCENTRANK.INC答え）］ワークシートに含まれています。上でも述べた通り、Googleスプレッドシートでは、有効桁数の取り扱いが異なるので0.773と表示されます。

　これらの関数の違いは、PERCENTRANK.EXC関数では0％と100％を除いた範囲で順位を求め、PERCENTRANK.INC関数では0％と100％を含めた範囲で順位を求めるということです。……が、それだけだと意味が分からないですね。80点など、元のデータに存在しない値を指定した場合の順位の求め方についても謎です。そこで、詳細な計算方法を後のコラムにまとめておきました。先を急ぐ方はコラムを飛ばしてもらっても構いません。

実際のところ、データ数が多ければ、どちらの関数を使ってもほぼ同じ結果になるので、順位を求めるという目的において、実用上での違いはほとんどありません。

コラム　PERCENTRANK.EXC関数とPERCENTRANK.INC関数の計算方法

　PERCENTRANK.EXC関数では、RANK.EQ関数と同じ方法で求めた昇順の順位をkとし、全体の個数をnとすると、k/(n＋1)でパーセント単位の順位が求められます。ただし、指定した値が元のデータに含まれない場合には、1つ下の値と1つ上の値の間で補間が行われます。

　例えば、図3のデータでは、80という値は元のデータに含まれていません。そこで、1つ下の値である78（昇順なら8位）と、1つ上の値である82（昇順なら10位）の間で補間を行います（図4）。

図4　補間の方法（同順位が1つの場合）
下位の順位からどれだけ離れているかを基に、パーセント単位での順位の幅を配分する。この例では、80という値は78から82のちょうど半分の位置にあるので、0.615から0.769までの幅を半分進んだ位置（＝0.692）が答えとなる。

　計算の手順を追いかけると以下のようになります。

• 計算の基となる下位と上位のパーセント単位での順位と幅を求める
  • 78点の順位は昇順で8位： k＝8, n＝12なので、k/(n＋1)＝8/13＝0.615 …… (a)
  • 82点の順位は昇順で10位： k＝10, n＝12なので、k/(n＋1)＝10/13＝0.769 …… (b)
  • (b)と(a)の幅： 0.769−0.615＝0.154 …… (c)
• 比例配分する
  • 上位と下位の値の差： 82−78＝4 …… (d)
  • 80点と下位の値の差： 80−78＝2 …… (e)
  • (d)と(e)の比： 2/4＝0.5 …… (f)
  • (a)＋(c)×(f)を求める： 0.615＋0.154×0.5＝0.615＋0.77＝0.692 ……(g)

　このように、同順位が1つだけであれば単純に補間すればいいのですが、同順位が複数個ある場合には、補間した値をさらに補間する必要があります。この例では、78点が2つあるので、図4の補間を行った後、さらに図5のような補間を行います。

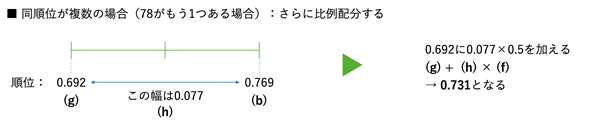図5　補間の方法（同順位が複数ある場合）
図4のように比例配分して求めた順位を下位の順位とし、さらに比例配分する。この例では、上で求めた0.692から0.769までの幅を半分進んだ位置（＝0.731）が答えとなる。

　計算の手順は以下の通りです。

• 78点がもう1つあるので、さらに比例配分する
  • 上位と(g)のパーセント単位での順位の差： 0.769−0.692＝0.077 …… (h)
  • (g)＋(h)×(f)を求める： 0.692＋0.077×0.5＝0.692＋0.0385＝0.7305 …… 小数点以下3桁までで四捨五入すると0.731（これが答え）

　PERCENTRANK.EXC関数やPERCENTRANK.INC関数では、有効桁数の既定値が小数点以下3桁となっているので、Excelの場合、特に何も指定しないと小数点以下3桁目より下位の桁は切り捨てられます。そのため、上で見た計算とは小数点以下3桁目の値が異なることがあります（PERCENTRANK.EXC関数の場合、0.7305の最後の桁が切り捨てられるので、結果は0.730となります）。

　一方の、PERCENTRANK.INC関数では、RANK.EQ関数と同じ方法で求めた昇順の順位をkとし、全体の個数をnとすると、(k−1)/(n−1)でパーセント単位の順位が求められます。やはり、指定した値が元のデータに含まれない場合には、1つ下の値と1つ上の値の間で補間が行われます。補間の方法はPERCENTRANK.EXC関数と同じです。

　サンプルデータの［計算方法］ワークシートには上記の手順で計算した例と、PERCENTRANK.EXC関数やPERCENTRANK.INC関数での検算結果が含まれています。手順はかなり長いですが、詳しく知りたい方はぜひご参照ください。

上位10％に入るには何点取ればいい？

　PERCENTRANK.EXC関数やPERCENTRANK.INC関数では、ある点数が全体の中の何パーセントの位置にあるかを求めましたが、逆に、全体の中の何パーセントの位置にいるには何点取ればいいかを知りたいこともあるでしょう。例えば、上位10％に入るには何点取ればいいか、といった場合です。

　上位10％の位置を知るには、下位から90％の位置を求めます。利用する関数は、PERCENTILE.EXC関数とPRECENTILE.INC関数です。サンプルファイル（06c.xlsx）をこちらからダウンロードし、［上位10％（PERCENTILE.EXC）］ワークシートを開いて以下の操作を行いましょう。操作は動画でも解説しています。手順を丁寧に追いかけたい方はぜひご視聴ください。

動画3　Excelでパーセント単位での順位からその位置の値を求める

　図6にPERCENTILE.EXC関数を入力する手順を示します。

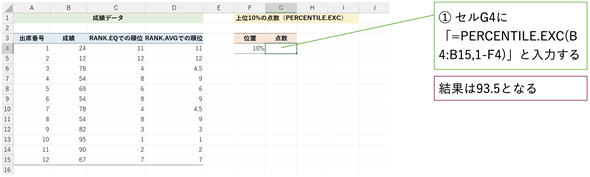図6　上位10パーセントの位置の点数を求める（PERCENTILE.EXC関数）
［上位10％（PERCENTILE.EXC）］ワークシートを開き、セルG4に「=PERCENTILE.EXC(B4:B15,1-F4)」と入力して順位に対応する点数を求めよう。
作成例は［上位10％（PERCENTILE.EXC答え）］ワークシートを参照。PRECENTRANK.EXC関数で求められる位置の最小値より小さい値や、最大値より大きい値を指定するとエラーになることに注意。

　PERCENTILE.EXC関数の第1引数にはデータの範囲を、第2引数には下位からの割合（パーセント）を指定します。この場合は上位10％に当たる値を求めたいので、第2引数の指定は、1から10％を引いて、下位から90％としています。関数の実行結果は93.5となります。つまり93.5点を取れば上位10％に入れるということです。

　PERCENTILE.INC関数の場合も、関数名が違うだけで、引数の指定方法は同じです。［上位10％（PERCENTILE.INC）］ワークシートを開いて、セルG4に「=PERCENTILE.INC(B4:B15,1-F4)」と入力してみてください。結果は89.2となります。

　これらの関数の違いも、PERCENTILE.EXC関数では0％と100％を除いた範囲で値を求め、PERCENTILE.INC関数では0％と100％を含めた範囲で値を求めるということです。これについては、前回説明した四分位数を求めるためのQUARTILE.EXC関数やQUARTILE.INC関数の計算方法と同様です。四分位数の場合は25％や75％を指定して計算しましたが、PERCENTILE.EXC関数やPERCENTILE.INC関数ではそれ以外の値も指定できるというわけです。詳細については、前回のコラムで解説しているので、そちらをご参照ください。

　このようにして得られた値をパーセンタイル値と呼びます。図6の例であれば、93.5が90パーセンタイル値ということになります。PERCENTILE.EXC関数やPRECENTILE.INC関数の第2引数に25％を指定した場合は第1四分位数が、75％を指定した場合は第3四分位数が求められます。それぞれQUARTILE.EXC関数やQUARTILE.INC関数の第2引数に1や3を指定した場合と同じ結果です。なお、PERCENTILE.EXC関数とPRECENTILE.INC関数についても、データ数が多ければ、ほぼ同じ値が返されるので、位置を求めるという目的において、実用上での違いはほとんどありません。

　前回紹介した統計ソフトのR（オープンソースで無料の統計解析向けプログラミング言語およびその開発実行環境）のquantile関数は、実は四分位数だけを求める関数ではなく、パーセンタイル値を求めるのにも使えます。その場合、第2引数に下位からの割合（パーセント）を指定します。引数にtype=6を指定するとPERCENTILE.EXC関数と同じ計算が行われ、type引数を指定しないとPRECENTILE.INC関数と同じ計算が行われます。

　これまでに見てきた関数は、全て順位を基にしたものです。しかし、試験の成績などの間隔尺度のデータは平均値の近くに値が集まっているのが一般的なので、単純に順位や比率で表すよりも、分布を反映したような値を求めたいこともあると思います。例えば、平均点が60点の試験であれば、60点から70点あたりには多くの人がいますが、同じ10点の幅でも90点から100点の人はそれほど多くないと考えられます。そこで、分布を想定し、どの位置までにどれぐらいの人がいるかを求めていくことにします。

平均値と標準偏差の間にどれぐらいの人がいるの？

　身長や知能テストの成績、各種測定値の誤差などは、一般に正規分布と呼ばれる分布に従う（当てはまる）ものと考えられます。正規分布とは、以下の式で表される分布です。

　πは円周率、μが平均値（母集団の平均）、σは標準偏差（母集団の標準偏差）です。exp(X)は、自然対数の底e≈2.71821のX乗を表します。

　この式の意味については、ここでは詳しく触れません。まずは、後で見るグラフをきちんと読み取れるようにしておきましょう。なお、式の意味は「AI・機械学習の数学入門」の第14回で詳しく解説しています。興味のある方はぜひご参照ください（動画での説明もこちらにあります）。

　数式だけではイメージが湧かないかもしれないので、(1)式を基に作成したグラフを眺めてみましょう。ここでは、令和元（2019）年の国民健康・栄養調査（厚生労働省）の結果（Excelファイルのダウンロード）から引用した20歳代男性の身長の平均値と標準偏差を利用します。平均値は171.5で、標準偏差は6.6となっています（以下、身長のデータは全てこの資料から引用しています）。

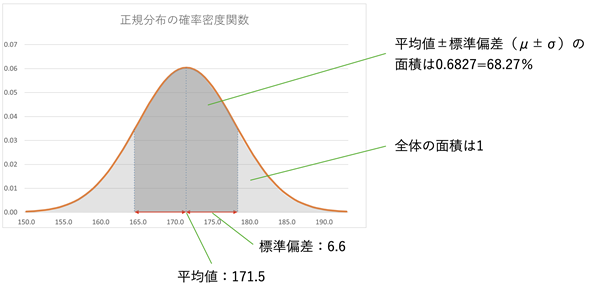図7　正規分布のグラフ（確率密度関数）
このグラフ（オレンジの線）は正規分布の確率密度関数と呼ばれる。確率密度関数は、平均値の位置で山が最も高く、左右に裾野が広がる形になっている。横軸の値は、理論的には−∞〜∞までだが、取り得る値の範囲に限定して考えるのが一般的（身長なら広く見積もって0cm〜300cm、試験の成績なら0〜100など）。縦軸の値については後述。

　図7にも示しましたが、正規分布では、グラフとX軸で囲まれた範囲（アミカケ全体）の面積は1、つまり100％となります。また、μ±σの範囲（アミカケが濃くなっている部分）に全体の68.27％が含まれ、μ±2σの範囲に全体の95.45％が含まれることが分かっています。重要なことなので、箇条書きでもう一度整理しておきます。

• μ±σの範囲： 全体の68.27％
• μ±2σの範囲： 全体の95.45％

　この例であれば、全体の68.27％が身長164.9cmから178.1cmであるということが分かります。また、全体の95.45％が158.3cm〜184.7cmとなります。

　確率密度関数を見る上での留意点が1つあります。それは、確率密度関数の縦軸の値は確率ではないということです。例えば、x=170.0のとき、f(x)の値は0.0589ですが、これは身長が170cmである確率が0.0589だということではありません（この値は次に示す累積分布関数の微分係数に当たる値です）。

　xの値に対するf(x)までの面積を関数F(x)として表すと、図8の右のグラフができます。この関数は累積分布関数と呼ばれます。全体の面積が1なので、F(x)の値は、xまでの値を取る確率になることが分かります。正規分布などの連続分布では、値xに対する確率は求められませんが、ある値xまでの確率は累積分布関数によって求めることができます。

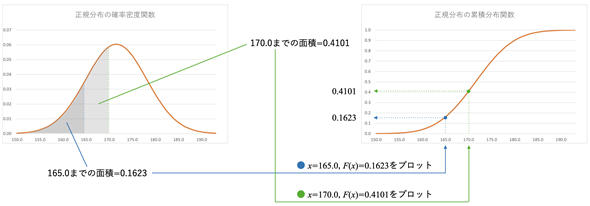図8　正規分布のグラフ（確率密度関数と累積分布関数）
例えば、x＝165.0までの面積（左のグラフの濃いアミカケの面積）は0.1623となっており、x＝170.0までの面積（左のグラフのアミカケ全体の面積）は0.4101となる。これらの値をプロットしていったものが、右側の累積分布関数のグラフとなる。これは確率密度関数を積分した値をプロットしたものと考えられる。

　累積分布関数では、横軸がxを表し、縦軸が累積確率F(x)を表します。従って、この例では、横軸が身長、縦軸がその身長までの人の割合となります。身長165.0cmまでの人は全体の16.23％、170.0cmまでの人は全体の41.01％であることが累積分布関数のグラフから読み取れます。

20歳代の男性で身長175cmなら全体のどのあたり？

　ここまでで、グラフの見方は分かったと思いますが、身長が170.0cmのときの確率密度関数の0.0589という値や、そのときの累積分布関数の0.4101という値はどうやって求められるのでしょうか。(1)式を思い出してください。(1)式のxに170.0を代入すれば、確率密度関数f(x)の値0.0589が求められます。また、その式を−∞〜170.0まで積分すれば、累積分布関数F(x)の値0.4101が求められます。とはいえ、この計算はかなり難しいですね。例えば、次に身長が175.0cmのときの累積分布関数の値を知りたい（身長が175.0cmなら全体のどのあたりの位置にいるかを知りたい）と思っても、簡単には計算できそうにありません。

　そこで、ExcelのNORM.DIST関数の出番です。この関数を使えば、xの値と平均値μ、標準偏差σを指定するだけで、確率密度関数や累積分布関数の値が求められます。では、サンプルファイル（06d.xlsx）をこちらからダウンロードし、［累積分布の値］ワークシートを開いて以下の操作を行いましょう。具体的な操作については動画でも解説しています。

動画4　Excelで正規分布の確率密度関数や累積分布関数の値を求める

　図9にNORM.DIST関数を入力する手順を示します。

図9　身長175cmの人がどのあたりにいるかをNORM.DIST関数で求める
［累積分布の値］ワークシートを開き、セルD4に「=NORM.DIST(A4,B4,C4,TRUE)」と入力しよう。結果は0.7020となる。
作成例は［累積分布の値（答え）］ワークシートを参照。

　NORM.DIST関数の引数には、xの値、平均値、標準偏差、関数の形式（FALSEなら確率密度関数、TRUEなら累積分布関数）を指定します。この例では、セルD4に「=NORM.DIST(A4,B4,C4,TRUE)」と入力すれば、0.7020という結果が得られます。つまり、身長175cmの人は身長の小さい方から数えて全体の70.2％の位置にいることが分かります。ここでは、確率密度関数の値を求めても「どの位置にいるか」という目的には合わないので、最後の引数にTRUEを指定して累積分布関数の値を求めました。

　実は図7や図8のグラフは、NORM.DIST関数に150〜193までの値を1刻みで順に指定していき、確率密度関数の値や累積分布関数の値を求めて、折れ線グラフにしたものです（散布図を使っても作成できます）。グラフの作成例もサンプルファイル（06d.xlsx）の末尾にある［正規分布の確率密度関数］ワークシートと［正規分布の累積分布関数］ワークシートに含まれているので、興味のある方はご参照ください。

　なお、ここで求めた正規分布の累積確率は、左側確率または下側確率と呼ばれることもあります。また、1−累積確率は、右側確率または上側確率とも呼ばれます（正規分布以外の分布でも同じように呼ばれます）。

正規分布で全体の上位10％に入るための身長は？

　これまでに見てきた「身長が何cmならどのあたりの位置にいるのか」とは逆に「どのあたりの位置にいる人は身長何cmなのか」を知りたいこともあります。つまり、xの値からF(x)の値を求めるのとは逆にF(x)の値からxの値を求めたい、ということです。Excelにはそのような場合に使えるNORM.INV関数がちゃんと用意されています。

　では、先ほどダウンロードしたサンプルファイル（06d.xlsx）の［累積分布の逆関数］ワークシートを開いて以下の操作を行いましょう。この操作についても動画で解説しています。

動画5　Excelで正規分布の累積分布関数の逆関数の値を求める

　図10にNORM.INV関数を入力する手順を示します。

図10　全体の90％の位置に当たる身長はいくからを求める
［累積分布の逆関数］ワークシートを開き、セルD4に「=NORM.INV(A4,B4,C4)」と入力しよう。上位10％ということは、累積確率が90％の位置となる。関数の実行結果は179.96となる。
作成例は［累積分布の逆関数（答え）］ワークシートを参照。

　NORM.INV関数の引数には、累積確率、平均値、標準偏差を指定します。この例では、セルD4に「=NORM.INV(A4,B4,C4)」と入力すると、179.96という結果が得られます。つまり、上位10％に入るための身長は179.96cmであることが分かります。累積確率は、下位から何パーセントであるかを指定することに注意してください。

　言うまでもないことかもしれませんが、身長が上位10％に入っているかどうかというのは、あくまでも身長という物理的な値が大きいか小さいということであって、いいか悪いかという価値判断とは全く関係のないことです。

20歳代の170cmと60歳代の170cmではどちらが高身長？ 〜 偏差値

　ところで、20歳代で170cmの男性と60歳代の170cmの男性がいたとき、どちらの方が身長が高いと言えるでしょう。どちらも同じ値だから同じ、というのも一つの答えですが、20歳代男性の平均値が171.5cm、60歳代男性の平均値が167.4cmであることから、集団の中での位置を考えると、60歳代男性の170cmの方が高いと言えそうです。

　このことは、平均値の違いだけでなく、標準偏差の違いによっても変わってきます。実は、20歳代男性の平均値も30歳代男性の平均値も171.5ですが、20歳代男性の標準偏差は6.6、30歳代男性の標準偏差は5.5となっています。30歳代男性の方が、わずかですが平均値の近くに集まっているということですね。ということは、平均値から離れた値は30歳代男性の方が少ないことになります。例えば、175cmという身長であれば、30歳代男性の方が高いことになります。

　平均値や標準偏差が異なる集団同士でも、値がどのあたりの位置にあるかを比較したい場合に便利なのが、標準化変量や偏差値です。

　標準化変量は、データの値x_iから平均値μを引き、標準偏差σで割った値です。数式で表すと以下のようになります。

　このような計算を行うと、平均値が0、標準偏差が1の分布になるように値が調整されます。そうすれば、元の分布の平均値と標準偏差が異なっていても比較ができるというわけです。

　重回帰分析やロジスティック回帰などの機械学習でも、学習を効率よく行ったり、回帰式の係数を比較しやすくするために標準化を行うことがあります（こちらに詳しい説明があります）。

　ただ、標準化変量の値は日常の感覚ではちょっとイメージしづらい値になります。そこで、標準化変量に10を掛けて50を足した値もよく使われます。それが偏差値です。数式で表すと、以下のようになります。

　偏差値は平均値が50、標準偏差が10になります。試験の成績に比較的近いイメージなので、感覚的にも分かりやすいですね。

　では、20歳代男性で170cmの場合と60歳代男性で170cmの偏差値を求めてみましょう。先ほどダウンロードしたサンプルファイル（06d.xlsx）の［偏差値］ワークシートを開き、上の式に従って図11のように計算を行いましょう。平均値と標準偏差は表に入力されています。具体的な操作については動画でも解説しているので、ぜひご参照ください。

動画6　Excelで偏差値を求める

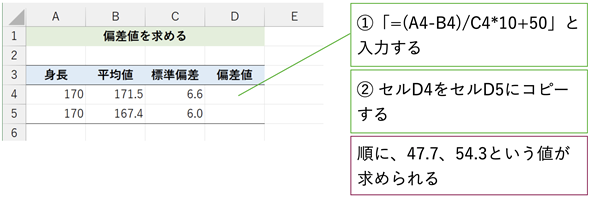図11　偏差値を求める
［偏差値］ワークシートを開き、セルD4に「=(A4-B4)/C4*10+50」という式を入力し、セルD5にコピーする。答えはそれぞれ47.7、54.3となる。
作成例は［偏差値（答え）］ワークシートを参照。

　セルD4に「=(A4-B4)/C4*10+50」という式を入力し、セルD5にコピーすると、それぞれの偏差値が求められます。結果は、20歳代男性で170cmの人の偏差値が47.7、60歳代男性で170cmの人の偏差値が54.3となるので、60歳代男性で170cmの人の方が（集団の中では）身長が高いと言えます。なお、図11では、数式通りに計算を行いましたが、Excelには標準化変量を求めるためのSTANDARDIZE関数も用意されています。従って「=STANDARDIZE(A4,B4,C4)*10+50」と入力しても同じ結果が得られます。関数を使うとかえって式が長くなりますが、標準化を行っているということはよく分かります。［偏差値（答え）］ワークシートにはSTANDARDIZE関数を使った例も含めてあります。

　偏差値は入試の難易度など、高校や大学のランク付けによく使われるので、あまりいい印象が持たれていないかもしれませんが、このように、異なる集団の間でも位置を比較するのに使えるとても便利な値なのです。

---

　……というわけで、今回は、各データの位置を知ることに焦点を当て、単純な順位だけでなく、パーセント単位での順位や偏差値を求めました。逆に、何パーセントの範囲に入るには何点を取る必要があるかといった計算の方法についても見てきました。次回以降、何回かに分けて、グラフを利用した可視化によってデータを分析する方法を見ていきます。

　次回は、規模や効果の大きさやその差を可視化するために使われる棒グラフについて、基本から応用までを見ることにします。棒グラフは誰もがすでに知っている基本中の基本ですが、意外な落とし穴もあります。そういったことについても触れることにします。では、次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の使いこなし方については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

順位を求めるために使った関数

RANK.EQ関数： 順位を求める（同じ値は同じ順位とする）

形式

RANK.EQ(数値, セル範囲, 順序)

引数

• 数値： 順位を求めたい値を指定する。
• セル範囲： データが入力されているセル範囲を指定する。
• 順序： 0を指定するか省略すると降順に、0以外の数値を指定すると昇順に並べたときの順位を返す（ExcelやGoogleスプレッドシートでは、0はFALSE、0以外はTRUEと見なされるので、降順の場合にはFALSEまたは省略、昇順の場合はTRUEと考えてもよい）。

RANK.AVG関数： 順位を求める（同じ値は上位と下位の平均とする）

形式

RANK.AVG(数値, セル範囲, 順序)

引数

• 数値： 順位を求めたい値を指定する。
• セル範囲： データが入力されているセル範囲を指定する。
• 順序： 0を指定するか省略すると降順に、0以外の値を指定すると昇順に並べたときの順位を返す（ExcelやGoogleスプレッドシートでは、0はFALSE、0以外はTRUEと見なされるので、降順の場合にはFALSEまたは省略、昇順の場合はTRUEと考えてもよい）。

パーセント単位での順位やパーセンタイル値を求めるために使った関数

PERCENTRANK.EXC関数： パーセント単位での順位を求める（0％と100％は含まない）

形式

PERCENTRANK.EXC(データの並び, 値, 有効桁数)

引数

• データの並び： データ全体を指定する。
• 値： パーセント単位での順位を求めたい値を指定する。
• 有効桁数： 結果を小数点以下何桁まで求めるかを指定する。指定した桁以降は切り捨てられる（Googleスプレッドシートでは四捨五入される）。省略すると3が指定されたものと見なされる。

PERCENTRANK.INC関数： パーセント単位での順位を求める（0％と100％を含む）

形式

PERCENTRANK.INC(データの並び, 値, 有効桁数)

引数

• データの並び： データ全体を指定する。
• 値： パーセント単位での順位を求めたい値を指定する。
• 有効桁数： 結果を小数点以下何桁まで求めるかを指定する。指定した桁以降は切り捨てられる（Googleスプレッドシートでは四捨五入される）。省略すると3が指定されたものと見なされる。

PERCENTILE.EXC関数： パーセンタイル値を求める（0％と100％は含まない）

形式

PERCENTILE.EXC(データの並び, 率)

引数

• データの並び： データ全体を指定する。
• 率： 求めたいパーセンタイル値の位置を0〜1の範囲で指定する。ただし、最小値の位置より小さい値や最大値の位置より大きな値を指定するとエラーになる。

PERCENTILE.INC関数： パーセンタイル値を求める（0％と100％を含む）

形式

PERCENTILE.INC(データの並び, 率)

引数

• データの並び： データ全体を指定する。
• 率： 求めたいパーセンタイル値の位置を0〜1の範囲で指定する。

正規分布の確率密度関数や累積分布関数を求めるために使った関数

NORM.DIST関数： 正規分布の確率密度関数や累積分布関数の値を求める

形式

NORM.DIST(値, 平均, 標準偏差, 関数の形式)

引数

• 値： 確率密度関数や累積分布関数のxに当たる値を指定する。
• 平均： 分布の平均値を指定する。
• 標準偏差： 分布の標準偏差を指定する。
• 関数の形式： FALSEを指定すると確率密度関数の値を求める。TRUEを指定すると累積分布関数の値を求める。

NORM.INV関数： 正規分布の累積分布関数の逆関数の値を求める

形式

NORM.INV(確率, 平均, 標準偏差)

引数

• 確率： 累積分布関数の累積確率（左側確率）を指定する。
• 平均： 分布の平均値を指定する。
• 標準偏差： 分布の標準偏差を指定する。

標準化のために使った関数

STANDARDIZE関数： 標準化変量を求める

形式

STANDARDIZE(値, 平均, 標準偏差)

引数

• 値： 標準化したい値を指定する。
• 平均： 分布の平均値を指定する。
• 標準偏差： 分布の標準偏差を指定する。

「やさしいデータ分析」