［NumPy超入門］内積、行列積からコサイン類似度までNumPyを使って試してみよう：Pythonデータ処理入門（1/2 ページ）

内積や行列積、アダマール積などさまざまな種類がある行列の積とそれらを計算する関数、2つのベクトル（行列）が似ているかどうかを判定できるコサイン類似度について触れてみよう。

[かわさきしんじ，Deep Insider編集部]

連載目次

連載概要

　本連載はPythonについての知識を既にある程度は身に付けている方を対象として、Pythonでデータ処理を行う上で必須ともいえるNumPyやpandas、Matplotlibなどの各種ライブラリの基本的な使い方を学んでいくものです。そして、それらの使い方をある程度覚えた上で、それらを活用してデータ処理を行うための第一歩を踏み出すことを目的としています。

ベクトルや行列の積にもいろいろある

　前回はNumPyが提供する多次元配列（numpy.ndarray）の最大値／最小値を得る方法はたくさんあることを見ました。それと同時にデータがないことを意味するnumpy.nanオブジェクトについても紹介をしました。

　今いったように多次元配列の最大値／最小値を得る方法はたくさんありますが、実は多次元配列同士の積を求める方法もたくさんあります。今回は主にその方法を紹介していきましょう。

　例えば、NumPyで多次元配列の積を求めるときには、以下のような値を計算することになります（以下は一部です）。

• スカラー倍
• 要素ごとの積（アダマール積）
• 内積
• 行列積

　スカラー倍というのはスカラー値とベクトル／多次元配列の積のことです。これは単純にベクトルや多次元配列の各要素にスカラー値を乗算したものが求める値となります。

スカラー倍

　要素ごとの積（アダマール積）とは、対応する要素同士（インデックス位置が同じ要素同士）を乗算したものが求める値になります。

アダマール積（要素ごとの積）

　内積は2つのベクトル（一次元配列）の内積（対応する要素同士を乗算したものの和）を計算します。

ベクトルの内積

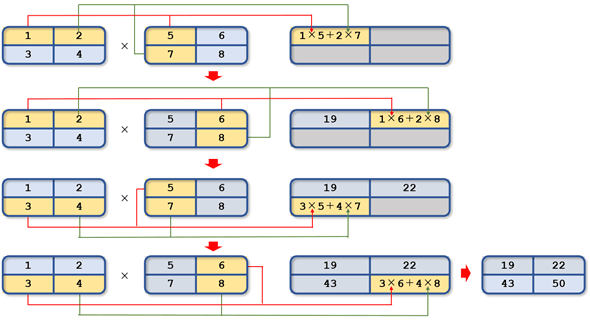
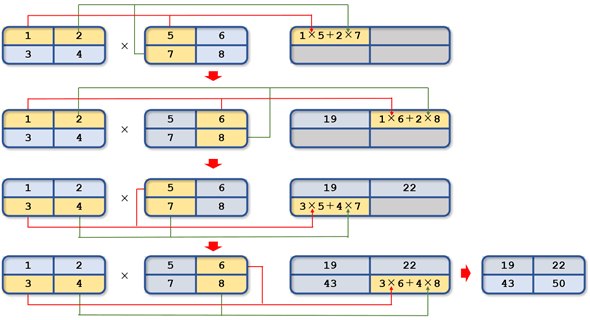
　行列積は言葉にはしづらいのですが、2つの行列（2次元配列）に対して以下のような計算を行います。

行列積

　まずは1つ目の配列の第1行と、2つ目の配列の第1行とで計算をします。このときには1つ目の配列で行の先頭に近い位置にあるものから、2つ目の列の先頭に近いところにあるものと順番に乗算されていきます。乗算した結果を全て足し合わせたものが結果の配列の第1行第1列の値になります。

　次は1つ目の配列の第1行と、2つ目の配列の第2列を対象に先ほどと同様な順序で各要素の乗算が行われます。そして、こちらも乗算した結果を全て足し合わせたものが第1行第2列の値になります。といった具合に1つ目の配列と2つ目の配列の各行と各列とで要素の乗算とその和を得て、結果の行列ができあがります。

　そして、それらの計算を行うために以下のような関数や演算子が用意されています。

方法	説明
numpy.multiply関数	スカラー倍、アダマール積を求める
numpy.matmul関数	内積（ベクトル同士の場合）、行列式（二次元配列同士の場合）
numpy.dot関数	スカラー倍（スカラー値と一次元以上の配列の場合）、内積（ベクトル同士の場合）、行列積（二次元配列同士の場合）
numpy.inner関数	スカラー倍（スカラー値とベクトル／配列の場合）、内積（ベクトル同士の場合）、最後の軸に沿って積の和を求める（二次元以上の配列同士の場合）
*演算子	numpy.multiply関数と同様
@演算子	numpy.matmul関数と同様
積を求める関数／演算子（一部）

　以下ではこれらの関数／演算子の使い方を簡単に見ていきましょう。

numpy.multiply関数

　numpy.multiply関数は2つの多次元配列の対応する要素同士を乗算した結果を返します。一方がスカラー値の場合は、多次元配列の各要素にスカラー値を乗算した結果を返します。両方がスカラー値であれば単にそれらを乗算した結果を返します。

　以下に例を示します。

import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

c = np.multiply(a, b)  # 二次元配列同士
print(c)
# 出力結果：
#[[ 5 12]
# [21 32]]

c = np.multiply(a, 2)  # 一方がスカラー値
print(c)
# 出力結果：
#[[2 4]
# [6 8]]

c = np.multiply(2, 3)
print(c)  # 6

numpy.multiply関数の使用例

　最初の例では二次元配列の対応する要素同士が乗算され、第1引数に指定した配列と同じ形状の配列が返されていることが分かります。次の例では、「np.multiply(a, 2)」としているので配列aの各要素の値が2倍されていますね。最後の例はスカラー値同士の乗算ですが、まあ普通は「c = 2 * 3」のように書くでしょう。

　というわけで、numpy.multiply関数を使う場面では、*演算子を使って次のようにも書けます（実行結果は省略します）。

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

c = a * b  # 二次元配列同士
print(c)

c = a * 2  # 一方がスカラー値
print(c)

c = 2 * 3
print(c)

numpy.multiply関数の代わりに*演算子を使っているところ

　多次元配列同士をnumpy.multiply関数で乗算する際に、両方の配列の形状が異なっていたら、いずれかの配列をより大きな形状の配列と同じ形状にブロードキャストできる必要があります。

a = np.array([[1, 2], [3, 4]])
b = np.array([2, 2])

c = np.multiply(a, b)
print(c)
# 出力結果：
#[[2 4]
# [6 8]]

c = np.multiply(b, a)
print(c)  # 上と同じ

ブロードキャストして形状をそろえられればnumpy.multiply関数で乗算可能

numpy.matmul関数

　numpy.matmul関数はベクトル（一次元配列同士）を2つ渡すとそれらの内積を、行列（二次元配列）を2つ渡すとそれらの行列式を計算します。三次元以上の場合の話はここでは取り扱わないことにしますが、三次元以上の配列同士をnumpy.matmul関数で乗算する際の振る舞いがnumpy.dot関数との振る舞いの差となることは覚えておきましょう。

　以下に例を示します。

a = np.array([1, 2, 3])
b = np.array([2, 2, 2])

c = np.matmul(a, b)  # ベクトルの内積を求める
print(c)  # 12

numpy.matmulを使ってベクトル（一次元配列）の内積を求める例

　この例ではベクトルを2つnumpy.matmul関数に渡しています。そのため、対応する要素同士を乗算したものの和（1×2＋2×2＋3×2＝11）が2つのベクトルの内積として求められています。

　一方、以下は2つの多次元配列を渡した例です。

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

print(a)
#[[1 2]
# [3 4]]

print(b)
#[[5 6]
# [7 8]]

c = np.matmul(a, b)
print(c)
#[[19 22]
# [43 50]]

numpy.matmul関数を使って行列（二次元配列）の行列積を求める例

　この場合は先ほど示した図と同様な計算が行われて、2行2列の配列が得られます。

行列積の計算（再掲）

　numpy.matmul関数の省略記法としては@演算子があります。これを使うと上のコードは次のように書き換えられます（結果は省略）。

a = np.array([1, 2, 3])
b = np.array([2, 2, 2])

c = a @ b  # ベクトルの内積を求める
print(c)

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

c = a @ b
print(c)

@演算子の使用例

　なお、この例では2つの二次元配列がどちらも同じ形状（2行2列）の正方行列でしたが、行列積はN行K列とK行M列のように、最初に置く行列の列数と次に置く行列の行数が等しければ求められます。このとき、行列積の形状はN行M列になります。

　以下に例を示します。

a = np.array([[1, 2, 3], [4, 5, 6]])  # 2行3列
b = np.array([[1, 0, 1], [0, 1, 0], [1, 0, 1]])  # 3行3列

print(a)
#[[1 2 3]
# [4 5 6]]

print(b)
#[[1 0 1]
# [0 1 0]
# [1 0 1]]

c = np.matmul(a, b)
print(c)
# 出力結果：
#[[ 4  2  4]
# [10  5 10]]

2行3列の行列と3行3列の行列の行列式を求める例

　この例では2行3列の行列と3行3列の行列をnumpy.matmul関数に渡しているので返された行列は2行3列になります。各要素の値は左上から右上、左下から右下の順に書くと「1×1＋2×0＋3×1＝4」「1×0＋2×1＋3×0＝2」「1×1＋2×0＋3×1＝4」「4×1＋5×0＋6×1＝10」「4×0＋5×1＋6×0＝5」「4×1＋5×0＋6×1＝10」のように計算されています。

　numpy.matmul関数を使う上での注意点としては行列の代わりにスカラー値を渡すことができない点があります。このため、この関数ではスカラー倍は求められません。