［データ分析］折れ線グラフで「変化」を可視化 〜 売り上げは本当に上がっているか？：やさしいデータ分析
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第8回。グラフを利用して時間的な変化を可視化する方法と、それに関連するさまざまな考え方を追いかけます。具体的には折れ線グラフを使いますが、データの取り扱い、結果の見方などに関して、考慮すべき点や見落としがちな点について見ていきます。
連載：
この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト（ExcelやGoogleスプレッドシート）を利用した作成例を紹介します。
必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
羽山博筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入（またもや金欠）。
読者の皆さんは、データを見るだけで、売り上げや成績が「上がっている」あるいは「下がっている」と即座に判断できるでしょうか。データ分析に慣れた人であれば、まずはデータをグラフ化して目視で確認します。図1は、ある生徒の成績をグラフ化した図です。
何の変哲もない、皆さんがよく使う「折れ線グラフ」ですね。意外に思われるかもしれませんが、折れ線グラフはデータ分析に必須で大活躍します。折れ線グラフを使えば、時間による売り上げや成績の変化が一目で分かるようになります。この記事では、折れ線グラフをどうやって役立てればよいかを詳しく説明します。
また、折れ線グラフの作り方がよくないと誤解を招くケースがあります。記事の後半では、誤解を避けるコツやさらなる応用の方法などを説明します。ぜひ無料会員登録して全文をお読みください。
この記事は、データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第8回です。第7回の棒グラフから、今回の折れ線グラフ、円グラフ／パレート図、ヒストグラム、ヒストグラム、第12回の散布図まで、1つずつ可視化の基礎を学んでいきます。これらグラフの目的と効用などについて、特別予告編で簡単に整理していますので、事前に確認しておくとより理解が深まるでしょう。可視化シリーズを続けて読んでグラフの使い分けをマスターしたい方は、次回を見逃さないために記事冒頭のボタンからメール通知に登録するのがお勧めです。
この記事で学べること
今回は以下のようなポイントについて、分析の方法や落とし穴を見ていきます。
- 折れ線グラフに潜む落とし穴 …… 簡単そうに見えて、見当外れなグラフに？
- 折れ線グラフでデータを比較 …… 世界の中で日本の地位はどう変化したか？
- 折れ線グラフにだまされるな …… 可処分所得は増えているのか？
- 折れ線グラフでトレンドをつかむ …… 移動平均で株価の動きを予測！
- 棒グラフと折れ線グラフの組み合わせ …… 規模の異なるデータの変化を可視化／比較！
折れ線グラフは小学4年生で学びますが、意外に奥が深いです。データ分析の基本なのでしっかりと身に付けておきましょう！ では、サンプルファイルの利用についての説明の後、本編に進みましょう。
サンプルファイルの利用について
本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントがあれば使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントがあれば使える無料のGoogleスプレッドシート（Google Sheets）をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、.xlsxファイルをGoogleドライブにアップロードしてから開いた上で［ファイル］メニューの［Google スプレッドシートとして保存］を実行してください（Googleスプレッドシート独自の機能を使っている場合は、ファイルを共有して参照できるようにします。その場合は、該当する箇所で使い方を記します）。
折れ線グラフに潜む落とし穴 〜 成績の変化を可視化、でもそれでいいの？
「この記事で学べること」で触れた最初のテーマからです。売り上げや成績、事故の件数など、時系列で並んださまざまなデータは折れ線グラフを使って可視化することにより、変化を捉えることができます。そこで、できるだけシンプルな例として、図2の成績データ（架空データ）を基にケーススタディーを行ってみましょう。折れ線グラフの作成なんて簡単と思われるかもしれませんが（確かに操作そのものは簡単ですが）、分析は簡単にいかないこともあります。折れ線グラフを作成し、グラフからどんなことが言えそうか考えてみましょう。サンプルファイルをこちらからダウンロードし、［成績］ワークシートを開いて取り組んでみてください。
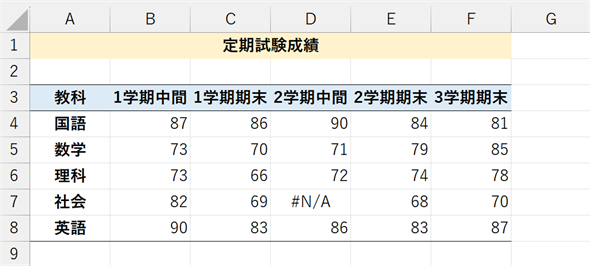図2 定期試験のデータこのデータを基に折れ線グラフを作成し、成績についての分析を行ってみよう。気付いたことをできるだけたくさん列挙してほしい。なお、社会の2学期中間試験は、その時間に体調を崩して試験を受けられなかったので、利用できる値がないことを表すエラー値#N/Aを入力してある。
折れ線グラフの作成に関しては、難しいところはありません。図3のようなグラフが作成できると思います。手順は、図3の後に箇条書きで示してありますが、動画でも詳しく解説しています。手順を一つ一つ追いかけたい方はぜひご視聴ください。
動画1 Excelでの折れ線グラフの作り方
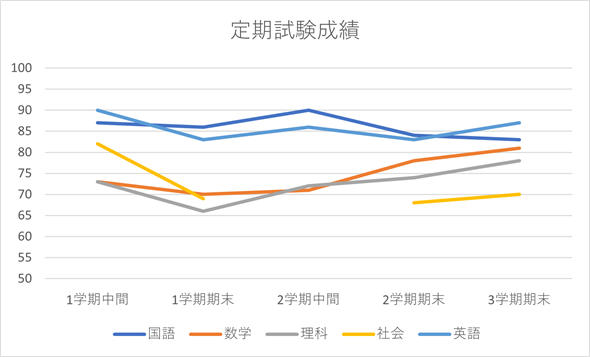図3 定期試験のデータを折れ線グラフにする素直に折れ線グラフを作成した結果。ただし、縦（数値）軸の最小値と最大値を変更し、グラフのタイトルとしてセルA1の値が表示されるようにしてある。このグラフを基に分析を行ってみよう。社会の2学期中間試験のデータがないので線がつながらないが、今のところは線をつながなくてもよい（線をつなぐ方法については後述）。
グラフ作成の手順は以下の通りです。
- セルA3〜F8のいずれかのセルをクリックする（アクティブセル領域がグラフデータの範囲となる）
- ［挿入］タブを開き、［折れ線／面グラフの挿入］−［折れ線］を選択する
- Googleスプレッドシートの場合は、メニューから［挿入］−［グラフ］を選択し、［グラフエディタ］の［グラフの種類］のリストから［折れ線グラフ］を選択する
最初の手順でグラフ化する範囲を指定していないことが気になる方もおられるかもしれません。Excelでは、グラフ作成や並べ替え、集計などの際に特に範囲を指定しないと、アクティブセル領域が指定されたものと見なされます。アクティブセル領域とは、アクティブセルを含み、空白のセルで囲まれた範囲です。図1の例であれば、セルA3〜F8を選択しなくても、その範囲のいずれかのセルをクリックしておけばいいというわけです。
続けて、縦（数値）軸の最小値と最大値を指定し、グラフのタイトルを変更します。
- 縦（数値）軸を右クリックし、［軸の書式設定］を選択する
- ［最小値］に50を入力し、［最大値］に100を入力する（縦（数値）軸の目盛りが変わる）
- Googleスプレッドシートの場合は［グラフエディタ］の［カスタマイズ］をクリックし、［縦軸］をクリックして［最小値］に50を入力し、［最大値］に100を入力する
- グラフ中の「グラフ タイトル」をクリックして選択する
- 「グラフ タイトル」をもう1回クリックして、「定期試験成績」という文字列を入力する
- Googleスプレッドシートの場合はグラフのタイトル部分をダブルクリックし、「定期試験成績」という文字列を入力する
グラフのタイトルは、上の手順のように直接入力しても構いませんが、デスクトップ版のExcelでは、以下の操作でセルの内容をグラフのタイトルに表示できます。
- 「グラフ タイトル」をクリックして選択する
- 数式バーをクリックして入力できるようにする
- 「=」を入力する
- セルA1をクリックする
このように操作すれば、セルA1に入力されている「定期試験成績」という文字列がグラフのタイトルとして表示されるようになります。また、セルA1の内容を変更すれば、グラフのタイトルもそれに合わせて変更されます。
図2を見ると「定期試験成績」という文字列はセルC1〜D1辺りに表示されているように見えますが、データはA1に入力されています。これはセルA1〜F1の範囲内で中央にそろえるように設定してあるからです。デスクトップ版のExcelの場合、選択範囲内で中央にそろえるには、セルA1〜F1を選択し、［ホーム］タブにある［配置］グループの［配置の設定］ボタン（右下にある小さな矢印が表示されたボタン）をクリックします。［セルの書式設定］ダイアログの［配置］タブが表示されるので、［横位置］のリストから［選択範囲内で中央］を選択します。
なお、セル結合を行っても同様の表示にできますが、セル結合を行うと列の移動／挿入や並べ替えなどがうまくいかなくなることがあります。
さて、図3のグラフからどのようなことに気づいたでしょうか。以下、オレンジ色の部分をクリックまたはタップすると、読み取れることやそれに対する考察などが表示されます。まずは自分で考えてから表示してみてください。
- 1学期の期末試験では成績が下がっている → 中間試験の成績がよかったので、油断した？
- 2学期から3学期にかけて成績が上がっている → 成績が下がったので奮起した？
- 理科系よりも文科系の方が好成績。ただし、社会は1学期中間を除いてあまりよくない → いわゆる暗記科目は苦手？
- 数学と理科は成績が上がってきている → 何かコツをつかんだのか？ 奮起のたまものか？
ここまではまだまだウオーミングアップです。上に示した箇条書きの項目は高校生でも（というか小学生でも）容易に思いつくことと思います。しかし、この連載の第1回は「高校生に負けない」といううたい文句から始まりました。ここで、上の分析を全否定して、高校生をぎゃふんと言わせてみましょう。以下のオレンジ色の部分をクリックまたはタップして、どういったことが考えられるかを見てみましょう。ここでも自分で考えてから表示してみてください。
- 試験の難易度が教科によって異なるかもしれない → 理科系よりも文科系が好成績とは一概には言えない
- 同じ教科でも中間試験や期末試験など、期によっても難易度が異なるかもしれない → 成績が上がっているとか下がっているとは一概には言えない
例えば、1学期には数学と理科の成績があまり良くなく、2学期以降は成績が上がっているようです。しかし、1学期の試験は難しい試験だったので、全体的に成績がよくなかったからかもしれません。そのため、2学期からは易しめの問題になったのかもしれません。
では、どうすればより適切な分析ができるでしょうか。それには、この連載の第6回で解説した偏差値を使うといいでしょう。クラスあるいは学年の平均値と標準偏差を基に偏差値を求めれば、教科ごと、期ごとの比較ができます。やはり架空のデータですが、クラスの平均値と標準偏差を含む［偏差値グラフ］ワークシートを用意してあるので、参考にしてください。
素点や偏差値を使わずに、クラスや学年での順位を使って折れ線グラフを作るという手もあります。
偏差値の求め方はすでに第6回でやった通りで、グラフの作成方法は上で見たのと同じなので、結果だけ示しておきます（図4）。この例では、社会を除き、全般的に文科系、理科系の差はなさそうです。
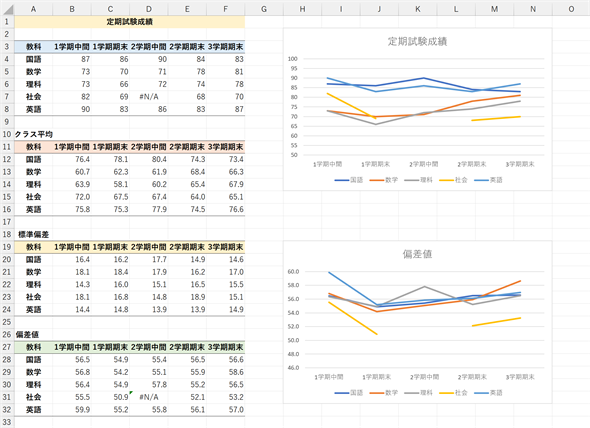図4 定期試験の偏差値を折れ線グラフにするセルB28に「=(B4-B12)/B20*10+50」と入力し、セルF32までコピーすると全ての偏差値が求められる。グラフにすると、1学期中間は英語をはじめとして全般的に好成績だが、1学期の期末に下降。2学期以降は徐々に回復。特に数学は素点でも偏差値でも上昇傾向。社会は1学期期末以降あまり良くないように思われる。しかし、社会以外は素点ほどには文科系、理科系の差はない。理科は素点では上昇傾向にあるが、偏差値を見ると浮き沈みがある。2学期中間の好成績はたまたまヤマが当たったのか、興味のある単元が試験範囲だったのかもしれない。
さて、懸案事項となっていた、欠損値を線でつなぐ方法を紹介しておきましょう。手順を箇条書きで示しておきます。意外に知られていない操作です。結果の図は単に社会の線がつながるだけなので省略します。
- グラフを選択し、［グラフのデザイン］タブをクリックする
- ［データの選択］ボタンをクリックする
- ［データソースの選択］ダイアログが表示されるので、［非表示および空白のセル］ボタンをクリックする
- ［非表示および空白のセル］ダイアログが表示されるので、［空白セルの表示方法］の［データ要素を線で結ぶ］を選択し、［#N/Aを空のセルとして表示］のチェックをオンにする
- ［OK］ボタンをクリックして［非表示および空白のセル］ダイアログを閉じる
- ［OK］ボタンをクリックして［データソースの選択］ダイアログを閉じる
Googleスプレッドシートでは以下の操作になります。
- ［グラフエディタ］の［カスタマイズ］をクリックし、［グラフの種類］をクリックする
- ［null値を表示］のチェックマークをオンにする
コラム 連勝の後は連敗が来る？ 〜 平均値への回帰
プロ野球などのスポーツで、推しのチームが何連勝もして喜んでいると、その後なぜか負けが込んでくることがあるように思われます。極端な場合、10連勝の後に10連敗などということもありますね。実は、この現象は平均値への回帰と呼ばれます。たまたまいい成績を取ったとしても、長い目で見ると平均的な（実力を反映した）成績に落ち着くというわけです。
上の例では、1学期中間でいい成績を取ったことも、1学期期末で振るわなかったのも、たまたまかもしれません。「中間ではいい成績だったのに、期末はどうしたんだ。たるんでるんじゃないか」などと𠮟ったとしても、その後、成績が持ち直したのは𠮟った効果ではなく、単なる平均値への回帰かもしれません。にもかかわらず、親や指導者が「𠮟ると成績が上がる」と思い込んでしまうのは短絡的です。それでも成績が上がらなかったときに「成績が上がらなかったのは𠮟り方が足りないからだ」と、さらにエスカレートするのは、生徒にとっては不幸でしかありません。
世界の中で日本の地位はどう変化したか 〜 データは比較してこそ違いが見えてくる
ここまでは、分析の観点などを分かりやすく説明するために架空のデータを使ってきました。しかし、ケーススタディーとしてはリアリティーが足りないかもしれませんね。そこで、ここからは実際のデータを使って、可視化と分析に取り組むことにしましょう。試験の成績の例でも、他者との比較によって本質が見えてくることに気づかれたかと思います。そういった例を見ていきます。
皆さんは昨年（2022年）の日本の1人当たりGDP（国内総生産）はG7先進国首脳会議の中で第何位かご存じでしょうか。……と、急に聞かれても答えられる人はあまりいないと思います。IMF（国際通貨基金）の調査によると3万3822ドルで、実は第7位、つまり最下位です。ちなみに1988年（2万5575ドル）〜1996年（3万9164ドル）は第1位でした。
その地位の変化を可視化してみましょう。日本のデータだけを折れ線グラフにすると、上昇している／下降している／浮き沈みがあるといったことは分かります。しかし、他の国々と比較しないと、地位の変化は見えてきません。図5はG7に加えて、同じアジアの国ということで、中国と台湾、韓国を含め、1990年〜2022年までの1人当たりGDPを折れ線グラフにしたものです。
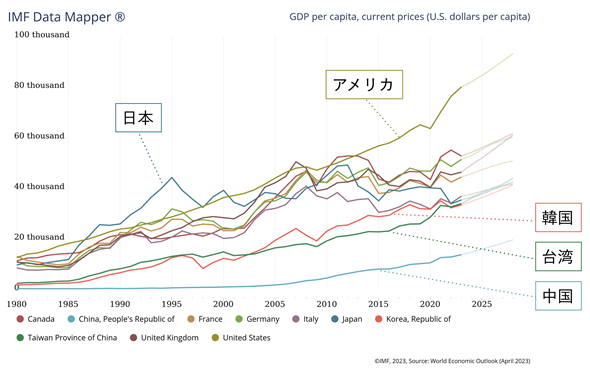図5 G7＋中国、台湾、韓国の1人当たりGDPの変化を折れ線グラフにするこのグラフは上で述べたIMFのWebサイトで作成したグラフに、幾つかの国名をラベルとして追加したもの。国や地域、年を選ぶだけで、ヒートマップや折れ線グラフが自動的に作成される。また、アニメーションも実行できる。2023年以降の点線は予測値。Excelのファイルをダウンロードして自分でグラフを作成することもできるが、こちらの方が手軽で便利。
グラフの色分けが微妙でかなり込み入っているので分かりにくいかもしれませんが、傾向としては、アメリカが1人勝ちの様相を示しています。ヨーロッパは波があるものの、イタリアを除き、2010年以降おおむね安定しています。残念ながら、日本は負け組のようです。中国、台湾、韓国もほぼ右肩上がりで、特に台湾と韓国は日本と同じ水準に達しています。中国はGDP全体ではアメリカに次いで世界第2位なのですが、人口が多いので1人当たりのGDPはかなり低くなっています。また、貧富の差も大きいようです。ちなみに、日本はGDP全体では世界第3位です。
日本が負け組に転落した理由としては、1900年代末期のバブル崩壊後の需要の低下や生産年齢人口の減少、生産性の伸び悩み（内閣府、平成27年度年次経済財政報告）、2000年代のアメリカでのITバブル崩壊の影響を大きく受けたこと（内閣府、世界経済の潮流／世界経済白書）などが挙げられているようです。筆者は経済に関しては門外漢なので、これ以上の言及は避けますが、比較することによって、時系列による変化だけでなく、日本の地位や立場のようなものが見えてくることが分かります。
可処分所得は増えているのか 〜 折れ線グラフは「切り取り」にご注意
ここからは、折れ線グラフに関する注意点や便利な使い方などをオムニバス的に幾つか紹介します。まず、切り取りによる印象操作についてです。
図6をご覧ください。これは、内閣府の「家計可処分所得・家計貯蓄率四半期別速報（参考系列）」（Excelファイル）を基に家計可処分所得のデータをグラフ化したものです。2021年は新型コロナ禍の影響が拡大してきたせいでしょうか、可処分所得が減少していますが、2012年から一貫して増加しています。なお、こちらのExcelファイルに、グラフ化に使ったデータだけをまとめてあります。Googleスプレッドシートの場合はこちらのサンプルファイルを開いて、メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください（縦軸の目盛りの設定を合わせてあるだけで、内容は同じです）。
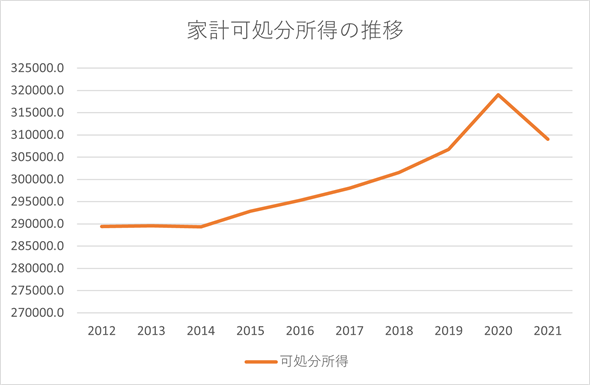図6 2012年から10年間の家計可処分所得の変化を折れ線グラフにする（単位：10億円）2012年から2021年にかけて、家計可処分所得（総額なので単位は10億円）はかなり増加しているように思われる。データには個人商店の値も含まれる。
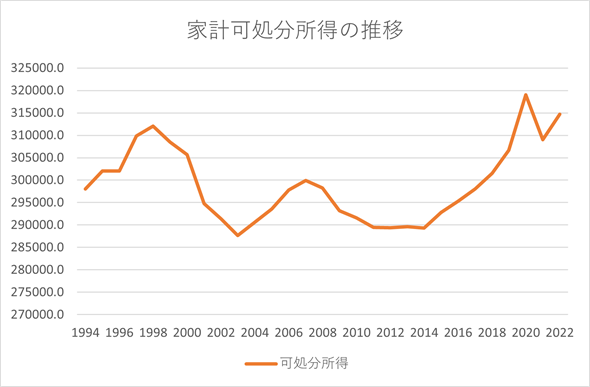
個人的には、生活が楽になったとは実感できないのですが、データを見る限り、可処分所得は増加しているように思われます。しかし、これは切り取りによる印象操作です。実は、基となるデータは1994年から2022年までの値が記録されています。その時期も含めてグラフを作成すると、図7のようになります。
図6は、家計可処分所得が増加していることを印象づけるため、一部のデータを切り取ってグラフ化したものになっていたということです。もちろん、もっと長い目で見れば、家計可処分所得は増加の傾向にあるのかも知れませんが、自分の主張に都合のいい部分だけを切り取るのはよくありませんね。
なお、上のグラフは名目値をプロットしたもので、実質の家計可処分所得は1994年以降ほぼ一貫して増加しています。ただし、実質値は、名目家計可処分所得を最終消費支出の名目値／実質値で割って求められた参考値なので、実質最終消費支出が大きくなると、実質家計可処分所得の値は大きくなってしまいます。また、上記のデータには貯蓄額などの値も含まれており、何かと興味深いのですが（貯蓄額はほぼ一貫して減っています）、ここは切り取りによって印象が変わるというお話なので、これぐらいにとどめておきます。
コラム 直感だけに頼らず、データに頼ろう
個人的なお話になってしまうのですが、筆者は最近のバイクブームに触発され、40年ぶりにバイクにまたがるようになりました。そういったリターンライダーが増加したせいか、毎日のようにバイクによる死亡事故がニュースになっています。筆者の感覚としては、バイクの事故が増えているような気がしています。
実際のところ、バイクの死亡事故は増えているのでしょうか。ちょっと調べてみました。警視庁による「30日以内交通事故死者の状況について」のPDFファイルを基に、二輪車に乗車していた人の死亡者数を折れ線グラフにしてみると、図8のようになります。こちらのExcelファイルに、グラフ化に使ったデータだけをまとめてあります。
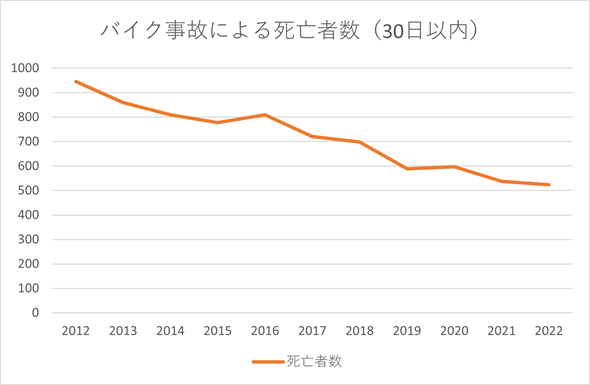図8 バイク事故による死亡者数の推移直感とは違って、バイク事故による死亡者数は減少の傾向にある。直感も重要だが、データによる理解も重要。かといって、油断は大敵。安全運転を心がけよう（ここには四輪車のデータは掲載していないが、四輪車とバイクの普及台数を考え合わせれば、当然のことながらバイク事故による死亡者の割合は大きい）。
データによると、バイクの死亡事故は増えているわけではなく、むしろ減っているようです。しかし、死亡事故が増えているように思うのはなぜでしょうか。理由の1つは認知バイアスです。バイクに再び乗るようになる前も同じようにニュースが報じられていたのかもしれませんが、その時には興味がなかったので、全く気にとめなかったのだと思われます。しかし、バイクに興味を持ち出すとバイク関連のニュースが強く印象に残るというわけです。理由のもう1つは、WebサイトやSNSのターゲティングにより、興味のあるニュースや情報がよく表示されるようになったからだと思われます。事故に関するニュースは筆者自身には警鐘を鳴らすものとして有益ですが、陰謀論や極端な考え方にハマってしまうのもこのためだと考えられています。直感も重要ですが、データをきちんと見ることも重要ですね。
ただし、警視庁のページによると、東京都ではバイクの事故は増えているようです。また、通勤時、50歳代、単独事故と右折時、頭部と胸部の損傷による死者が多いようです。頭部はヘルメットが外れた場合の死者が多く、胸部プロテクターを装着している人はわずかなようです（筆者はもちろん装着しています）。全体的に事故が減っているとはいえ、油断大敵です。バイクに乗る乗らないに関わらず、皆さんも交通にはどうぞお気を付けください。
株価の動きを予測する 〜 トレンドを見るには移動平均が便利
移動平均とは、何日分かの平均値を1日ずつずらしながら順に求めたものです。短期移動平均と長期移動平均を求めて折れ線グラフにすると、株価などの上昇／下落のトレンド（傾向）の変化が分かります。
図9は、Appleの株価（終値）の5日移動平均と15日移動平均を求め、折れ線グラフにしたものです。データはStooqというWebサイトで［Download data in csv file...］をクリックして、2023年6月1日〜8月31日までの3カ月間のデータを取得したものです。それを見やすくしたもの（Excelファイル）をこちらに置いておきました。グラフの作り方は図9の後に箇条書きで示してあります。動画でも解説しているので、手順を一つ一つ追いかけたい方はぜひご視聴ください。
動画2 Excelでの移動平均線グラフの作り方
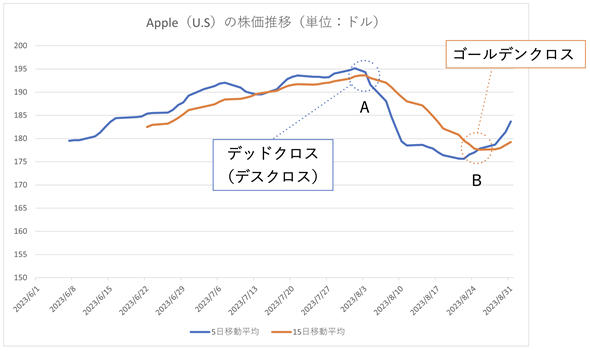図9 短期移動平均と長期移動平均（2023年6月1日〜8月31日のAppleの株価）短期（5日）移動平均と長期（15日）移動平均をプロットしたグラフ。短期移動平均が長期移動平均を上から下にクロスする箇所（Aの部分）を「デッドクロス」または「デスクロス」と呼び、株価が下がるシグナルとなる。逆に、短期移動平均が長期移動平均を下から上にクロスする箇所（Bの部分）を「ゴールデンクロス」と呼び、株価が上がるシグナルとなる。
図9のグラフの作り方は以下の通りです。
- 移動平均を求める手順：
- セルG8に「=AVERAGE(E4:E8)」と入力する
- セルG8をセルG67までコピーする
- セルH18に「=AVERAGE(E4:E18)」と入力する
- セルH18をセルH67までコピーする
- グラフを作成する手順：
- セルA3〜A67をドラッグして選択する
- セルG3〜H67を［Ctrl］キーを押しながらドラッグして選択する
- ［挿入］タブを開き、［折れ線／面グラフの挿入］−［折れ線］を選択する
Googleスプレッドシートの場合、移動平均の求め方は同じですが、グラフの作成時に縦軸の最小値と最大値を指定する必要があります。
- グラフを作成する手順：
- セルA3〜A67をドラッグして選択する
- セルG3〜H67を［Ctrl］キーを押しながらドラッグして選択する
- メニューから［挿入］−［グラフ］を選択し、［グラフエディタ］の［グラフの種類］のリストから［折れ線グラフ］を選択する。
- ［グラフエディタ］の［カスタマイズ］をクリックし、［縦軸］をクリックして［最小値］に150を入力し、［最大値］に200を入力する
図9を見ると、8月3日頃に短期移動平均が長期移動平均を上から下にクロスしています。長期移動平均のなだらかな変化に対して、短期移動平均が急に下がってきたということなので、その後株価が下落することが予測されます（この部分をデッドクロスまたはデスクロスと呼びます）。その後、8月24日頃には、短期移動平均が長期移動平均を下から上にクロスしています。こちらは、短期移動平均が急に上がってきたということなので、株価が上昇することが予測されます（この部分をゴールデンクロスと呼びます）。このように、短期移動平均と長期移動平均はトレンド（傾向）の変化を簡単に見るのに便利です。もちろん、デッドクロスやゴールデンクロスの兆候が現れたからといって、必ずしもその後株価がそれぞれ下落したり上昇したりするとは限りません（7月13日頃にデッドクロスの兆候がありますが、すぐに持ち直しています）。
規模の異なるデータの変化を可視化／比較する 〜 棒グラフと折れ線グラフの複合グラフを作る
前回、ちょっと先取りした話として時系列データのタイムラグについて説明しました。前回は、利用するグラフを棒グラフのみとし、縦（数値軸）の目盛りを1つだけに限定していたので、図10に示したサイトAの売り上げ（E列）とサイトBの1日後の売り上げ（G列）を棒グラフで簡易的に比較しました。
実のところ、サイトBのクリック数（D列）とサイトBの1日後の売り上げ（G列）をグラフにすれば、Webサイトにアクセスしてから購買行動に移るタイムラグが直接的に可視化できます。しかし、クリック数と売り上げはデータの規模（値の範囲）が異なるので、棒グラフだけではパターンが比較しづらくなります。そのような場合、第2軸を指定し、異なる目盛りを指定すれば、異なる規模のデータでも、パターンの変化が比較できるようになります。また、グラフを見やすくするためには、両方の系列を棒グラフにするのではなく、一方の系列を折れ線グラフにした「複合グラフ」の方が、より比較がしやすくなります。というわけで、サイトBのクリック数を折れ線グラフ（第2軸）として、1日後の売り上げを棒グラフとして表した複合グラフを作成してみたいと思います。
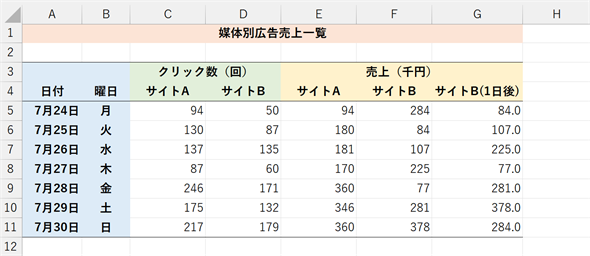図10 Webサイトの広告クリック数と売り上げサイトBの広告クリックが1日後の購買活動に結びついていることを可視化するには、サイトBのクリック数（D列）と、サイトBの1日後の売り上げ（G列）の変化のパターンを見るとよい。ただし、値の範囲が異なるので、集合縦棒グラフだけではパターンが比較しづらい。
図11が複合グラフの作成例です。操作の手順は図11の後に箇条書きで示してあります。こちらからExcelのブックをダウンロードし、［売上一覧］ワークシートを開いて操作してみてください。これについても、動画で操作の手順を解説しているので、一つ一つ追いかけたい方はぜひご視聴ください。なお、Googleスプレッドシートの場合はこちらのサンプルファイルを開いて、メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください（曜日の表示形式をGoogleスプレッドシートに合わせた形式にしてあるだけで、内容は同じです）。
動画3 Excelでの複合グラフの作り方
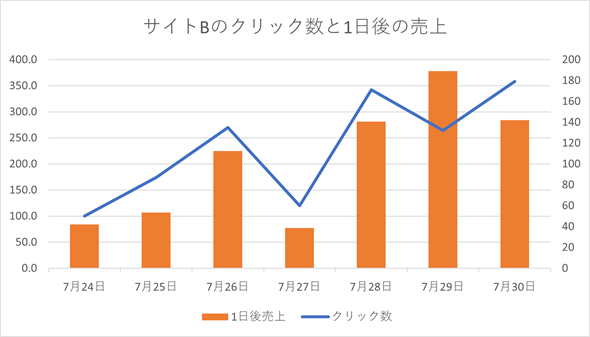図11 広告クリック数と1日後の売り上げを複合グラフにする複合グラフにすると、広告のクリック数（折れ線グラフ）と1日後の売り上げ（棒グラフ）が同じようなパターンになっていることがより明確に分かる。クリック数の目盛りは右側の第2軸となっていることに注目。第2軸を指定すれば、規模の異なるデータでもパターンを比較することができる。作成例は上でダウンロードしたファイルの［売上一覧（日付をずらしたグラフ）］ワークシートに含まれている。
グラフ作成の手順は以下の通りです。なお、この記事の執筆時点では、オンライン版のExcelの場合、複合グラフや第2軸を設定したブックをアップロードして表示／編集することはできますが、作成することはできないようです。
- セルA4〜A11をドラッグして選択する
- セルD4〜D11を［Ctrl］キーを押しながらドラッグして選択する
- セルG4〜G11を［Ctrl］キーを押しながらドラッグして選択する
- ［挿入］タブを開き、［複合グラフ］−［集合縦棒 − 第2軸の折れ線］を選択する
- Googleスプレッドシートでは、メニューから［挿入］−［グラフ］を選択し、［グラフエディタ］の［グラフの種類］のリストから［折れ線］の一覧にある［複合グラフ］を選択する
ここまでの操作で、クリック数が棒グラフ、1日後の売り上げが折れ線グラフの複合グラフが作られます。しかし、ここでは、逆にクリック数を折れ線グラフに、1日後の売り上げを棒グラフにしたいので、以下の操作でグラフの種類を変更する必要があります。
- 作成されたグラフをクリックして選択する
- ［グラフのデザイン］タブをクリックする
- ［グラフの種類の変更］ボタンをクリックする
- ［サイトB］の［グラフの種類］から［折れ線］を選択する
- ［サイトB］の［第2軸］のチェックボックスをクリックしてオンにする
- ［サイトB（1日後）］の［グラフの種類］から［集合縦棒］を選択する
Googleスプレッドシートでは、以下のような操作になります。
- ［グラフエディタ］の［系列］をクリックし、［すべての系列に適用］というリストから［サイトB］を選択する
- ［形式］の下の［種類］リストから［折れ線］を選択する
- ［軸］リストから［右軸］を選択する
- ［系列］の［サイトB］と表示されているリストをクリックし［サイトB(1日後)］を選択する
- ［形式］の下の［種類］リストから［縦棒］を選択する
凡例には、クリック数が［サイトB］、1日後の売り上げが［サイトB（1日後）］と表示されているので、ちょっと分かりにくいですね。そこで系列名も変えておきましょう。
- ［グラフのデザイン］タブをクリックする
- ［データの選択］ボタンをクリックする
- ［凡例項目（系列）］リストの［サイトB］をクリックし、［編集］ボタンをクリックする
- ［系列名］に「クリック数」と入力し、［OK］ボタンをクリックする
- ［凡例項目（系列）］リストの［サイトB（1日後）］をクリックし、［編集］ボタンをクリックする
- ［系列名］に「1日後売上」と入力し、［OK］ボタンをクリックする
- ［OK］ボタンをクリックして［データの選択］ダイアログを閉じる
Googleスプレッドシートでは、以下のような操作になります。
- グラフの上に表示されている凡例をクリックして選択する
- ［サイトB（1日後）］という凡例をダブルクリックして「1日後売上」と入力する
- ［サイトB］という凡例をダブルクリックして「クリック数」と入力する
作成されたグラフから、サイトBのクリック数と1日後の売り上げが同じパターンで増減していることが明確に読み取れますね。上でも述べましたが、複合グラフを利用して、左右にそれぞれの軸を設ければ、異なる規模のデータでもパターンの変化が比較できるようになります。
今回は、時系列での変化を見るために折れ線グラフを作成しました。その中で、自分の位置を確かめるためには比較することが重要であることも見ました。また、切り取りによる印象操作という落とし穴や、移動平均によりトレンドの変化をつかむ方法、複合グラフの第2軸を利用して規模の異なるデータの変化を比較する方法についても紹介しました。
次回は、重要度の可視化をテーマとしたケーススタディーを通して、円グラフやパレート図の作成や利用、読み解き方の留意点などを見ていきます。次回も、落とし穴や意外に知られていない機能などを紹介します。どうぞお楽しみに！
Copyright© Digital Advantage Corp. All Rights Reserved.
ITmediaはアイティメディア株式会社の登録商標です。