[NumPy超入門]Pythonで単回帰分析:手作業で計算してみよう:Pythonデータ処理入門
PythonとNumPyを使って手作業で、回帰分析のモデルを表す回帰式を求め、その決定係数を計算してみましょう。回帰分析が初めての方でもステップバイステップで計算内容が理解できます。同じ計算を手軽に行えるNumPyのpolyfit関数も解説します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
連載概要
本連載はPythonについての知識を既にある程度は身に付けている方を対象として、Pythonでデータ処理を行う上で必須ともいえるNumPyやpandas、Matplotlibなどの各種ライブラリの基本的な使い方を学んでいくものです。そして、それらの使い方をある程度覚えた上で、それらを活用してデータ処理を行うための第一歩を踏み出すことを目的としています。
前回はCalifornia Housingデータセット(カリフォルニアの住宅価格のデータセット)を基に相関係数を計算してヒートマップを作成したり、'MedInc'列(地域の所得を表すデータ)と'MedHouseVal'列(地域の住宅価格を表すデータ)を軸に散布図を作成したりして、これら2つのデータにはある程度の相関があるのではないかという話をしました。
今回は'MedInc'列と'MedHouseVal'列との関係を数式として表現してみます。いわゆる「単回帰分析」と呼ばれる手法で、所得からカリフォルニア州の住宅価格を予想できるような式を見つけようという考えです。
なお、前回は最後に外れ値を除去したデータをnew_data.csvファイルとして保存していますが、今回はこれを使います。実際に試してみようという方は、ここからダウンロードして使ってください。
単回帰分析とは
単回帰分析とは「回帰分析」と呼ばれるデータ分析手法の一つです。詳しくは前掲のリンクを参照してほしいのですが、簡単にいえば、あるデータと別のデータとの関係をモデル(数式)として表現し、分析するものです。モデルを表す数式のことを「回帰式」と呼ぶこともあります。
今の話でいうならカリフォルニア州の住宅価格はどんな要素から決定されるのかをモデル化しようというわけです。このデータセットには所得、築年数、部屋数などのデータと、住宅価格が含まれています。前回で作成したヒートマップや散布図からは、どうやらその候補となるのは所得(の中央値)ではないかという知見が得られています。
回帰分析においては、モデルで説明したい(数式を使って結果を求めたい)対象のことを「目的変数」と呼びます。この場合は、住宅価格がどうなるかを数式で表そうとしているので、住宅価格が目的変数です(「従属変数」「正解ラベル」などともいいます)。また、説明に使われる変数のことを、その名の通り、「説明変数」といいます(「独立変数」「特徴量」などともいいます)。ここでは、所得や築年数などが説明変数の候補といえます。が、既にお分かりの通り、ここでは説明変数として採用するのは所得データです。
単回帰分析とは、1つの説明変数のみを用いて目的変数を表そうという考えです。複数の説明変数があるときには、重回帰分析と呼ばれる手法が使われます(が、今回は取り上げません)。
今回は所得(の中央値。'MedInc'列)を使って、「y = a * x + b」つまり「住宅価格=傾き×所得+切片」という形でカリフォルニア州の住宅価格をモデル化してみます。データセットに含まれている所得と住宅価格の関係を一番適切に表現できるような、「傾き」と「切片」の値を調整することが目的です。
とはいっても、その精度が高くなることはないでしょう。以下は前回に作成した散布図です(外れ値を除外したもの)。
「y = a * x + b」という一次式は直線を表します。上の散布図にどんな直線を引けばよいのでしょうか。どんな直線を引いたところで、この散布図が示す所得の住宅価格の関係を完璧に説明できるものはないでしょう。
それでも、ここら辺りに直線を引くとよさそうだという予想ができませんか? 実際、一番よい具合の直線というものは存在します。例えばプロットされた各点と直線との距離の二乗を算出して、その値が一番小さくなるような直線がそうです。いわゆる「最小二乗法」のお出ましということになります。
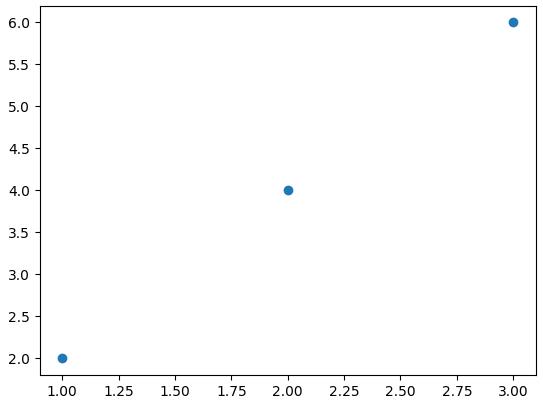
このまま、話を進めていくと、大変なことになりそうなので簡単にまとめておきます。データセットにデータ(例えば、所得と住宅価格の組み)がn個含まれているときに、その各点と直線との距離が最小となるような直線の傾き(「y = a * x + b」の「a」)は次の計算式で得られます。
ここで、x̂はX軸の値(所得)の平均値を、ŷはY軸の値(住宅価格)の平均値を、xiとyiは所得および住宅価格の個々のデータを表しています。Σは添字の(右下にある小さな)iを1からデータの個数であるnまで変化させながら、xiやyiと平均値との差を計算するなどしてから、それらの総和を求めるものです。
手作業で傾きを求めてみよう
と書いてもよく分かりませんよね。というわけで、実際に簡単なデータを使って試してみましょう。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([2, 4, 6])
ここではX軸の値は1、2、3の3つで、Y軸の値は2、4、6の3つです。Y軸の値はX軸の値を2倍したものになっているので、傾きは2です。また、X軸の値の平均値は2、Y軸の平均値は4となっていることも覚えておきましょう。
import matplotlib.pyplot as plt
plt.scatter(x, y)
plt.show()
これをグラフに散布図としてプロットしたのが以下です。
では、上の画像でやっていたことをPythonのコードにしていきましょう。まずはnumpy.mean関数で平均値を求めます。
x_mean = np.mean(x)
y_mean = np.mean(y)
print(f'{x_mean=}, {y_mean=}')
もちろん、それらは上で述べた通り、2と4です。次に、X軸の各座標から平均値を引いたものを二乗した値の和、X軸の各座標から平均値を引いたものとY軸の各座標から平均値を引いたものを乗算し、それらの和を求めます。
sum0 = (1 - 2) ** 2 + (2 - 2) ** 2 + (3 - 2) ** 2
sum1 = (1 - 2) * (2 - 4) + (2 - 2) * (4 - 4) + (3 - 2) * (6 - 4)
print(f'{sum0=}, {sum1=}')
X軸に注目すると、最初の座標(i=1)は「1」で平均値は「2」なので「1−2」を二乗した値である「1」が得られ、次の座標(i=2)は「2」なので「2−2」を二乗した「0」が得られ、最後の座標(i=3)は「3」なので「3−2」を二乗した「1」が得られます。その合計(sum0の値)は2になります(これが分母の値です)。Y軸についても同様に計算をすると、分子の値(sum1)は4になります。
最後に、分母の値で分子の値を割れば、傾きとして「2」が得られました。
a = sum1 / sum0
print(a)
切片については傾きが分かれば、「y = a * x + b」を変形して「b = y - a * x」とすることで簡単に算出できます。
というわけで、上と似たことをカリフォルニア州の住宅価格データセットについても行えば、先ほどの散布図に具合のよい直線を引くための傾きと切片が得られるということです。
カリフォルニア州の住宅価格データセットのモデルを作って回帰式を求めてみよう
では、前回作成したnew_data.csvファイルを読み込んで実際に回帰式を求めてみましょう。以下はCSVファイルを読み込んで、列にアクセスしやすいように辞書をセットアップするコードです。
data = np.loadtxt('new_data.csv', delimiter=',', skiprows=1)
with open('new_data.csv') as f:
header = f.readline()
columns = header.replace('# ', '').strip().split(',')
col = {k: v for v, k in enumerate(columns)}
print(col)
次にデータセットから'MedInc'列の値をX軸の値として変数xに、'MedHouseVal'列の値をY軸の値として変数yに取り出します。続けて、先ほどと同様な処理を行う関数を定義します。名前は「fit」としました(実はNumPyには傾きと切片の値を計算してくれる関数として、numpy.polyfit関数やnumpy.polynomial.polynomial.polyfit関数などがあります。また、scikit-learnのLinearRegressionクラスにもfitメソッドがあることから、ここでは関数名として「fit」を採用しています)。
x = data[:, col['MedInc']]
y = data[:, col['MedHouseVal']]
def fit(x, y):
x_mean = np.mean(x)
y_mean = np.mean(y)
x_part = x - x_mean
y_part = y - y_mean
xy = x_part * y_part
xx = x_part * x_part
sum_xy = sum(xy)
sum_xx = sum(xx)
a = sum_xy / sum_xx
b = y_mean - a * x_mean
return (a, b)
fit(x, y)
fit関数の最初の2行は平均値を求めているだけですから説明の必要はないでしょう。次の2行は、先ほどは項ごとに手作業で求めていたX軸やY軸の各値から平均を引くという作業を二度の引き算で終わらせています。NumPyではベクトルや行列の加減乗除を簡潔で分かりやすいコードとして記述できるのが実感できますね。
次の2行ではΣの中身を計算しています。1行目は分子となる部分の計算です。2行目は分母となる部分の計算です。そして、sum関数でそれらの和を求めています。最後に分母で分子を割って、得られた傾きを使って切片の値を求めたら、それらを戻り値として返送するだけです。
実行結果を以下に示します。
傾きは「0.4085」くらい、切片が「0.4214」くらいという結果が得られました。この値を用いた「y = 0.4085 * x + 0.4214」がこのモデルを表す回帰式といえます。では、この式を使って、散布図の上に直線をプロットしてみましょう。
a, b = fit(x, y)
plt.scatter(x, y, s=5)
plt.axline((x[0], a * x[0] + b), slope=a, color='red')
plt.show()
実行結果は次の通りです。
筆者が思っていたのとちょっとチャウという気もしますが(もうちょっと左下から、もうちょっと傾きが大きな直線が引かれると予想していました)、まあまあこんなものかもしれませんね。
決定係数を求めてみよう
先ほどの画像からはある地区の所得の高低だけでは、その地区の住宅価格がどうなるかを強く決定することにはなりそうもありません。実際に所得が住宅価格にどの程度影響しているかは「決定係数」という値で数値化できます(R2とも呼ばれます)。
詳しい説明は前掲のリンク先を参照していただくとして、決定係数の一般的な定義は次のようなものです。
式の右側の分数部分について簡単に説明しておきましょう。分母となる部分は目的変数の個々の値(実際に観測された値、観測値)からその平均を引いたものを二乗した総和です('MedHouseVal'列の個々の値から平均値を引き、その値を二乗して、総和を求めます。全平方和)。分子となる部分にあるfiという値は、先ほど得られたモデル(傾きと切片で表現される回帰式)にxの値(とは所得です)を入力したときに得られる推測値のことです。つまり、分子は推測された値と目的変数の実際の値との差(残差)を二乗した値になります(残差平方)。
決定係数は1に近いほど、観測値と推測値との乖離(かいり)が少ないことを示します。つまり、その説明変数が目的変数に強く影響しているといえるでしょう(寄与率と呼ぶこともあります)。
これを関数として定義したものが以下のコードです。
def calc_r2(y, f):
y_mean = np.mean(y)
y_f = (y - f) ** 2
y_yhat = (y - y_mean) ** 2
return 1 - sum(y_f) / sum(y_yhat)
この関数は目的変数('MedHouseVal'列の値)とモデルによる推測値(傾きaと切片bが得られているのでv = a * x + bで計算可能)を受け取り、上記の定義に従って決定係数を計算しています。
実際に決定係数を求めているのが以下のコードです。
v = a * x + b
r2 = calc_r2(y, v)
print(r2)
実行結果を以下に示します。
結果を見ると、その値は0.42程度です。微妙過すぎてなんといえばよいのか分かりません(笑)。所得が住宅価格に影響は与えているかもしれないが、それほど大きな影響はないくらいの値かもしれませんね。
NumPyが提供する機能を使ってモデルを求めてみよう
ここまでは自分で関数を定義して、回帰式「y = a * x + b」のaとb(傾きと切片)を求めていましたが、もちろん、NumPyにはそうした機能が備わっています。ここではその一つとして、numpy.polynomial.poynomial.polyfit関数を紹介しましょう。
以下にこの関数の構文を示します(抜粋)。
numpy.polynomial.polynomial.polyfit(x, y, deg)
3つあるパラメーターのうち、xとyには自分で定義したfit関数と同様にX座標とY座標となる値を渡します。degには単回帰分析では1を渡します。
実際にこれを呼び出して、傾きと切片を求めてみましょう。関数呼び出しだけで終わりです。
result = np.polynomial.polynomial.polyfit(x, y, 1)
print(result) # [0.42141751 0.4084746 ]
実行結果を以下に示します。
ただし、ここで少し気を付けてほしいところがあります。それは、こちらの関数では次元の低い方から高い方へという順番で係数が返されているところです。これは一次式なので切片(0次の係数)と傾き(1次の係数)の順で返されていますが、二次式であれば0次、1次、2次の順に係数が返されます。
NumPyには以前からnumpy.polyfit関数があり、自作のfit関数と同様な順序で係数を返送していました(むしろ、fit関数がnumpy.polyfit関数に合わせていました)。しかし、NumPy 1.4以降では、numpy.polyfit関数は古いAPIとされています。その代わりとして上で紹介したnumpy.polynomial.polynomial.polyfit関数が使えます。機械的に置き換える際には気を付けるようにしましょう。
また、numpy.polynomial.Polynomial.fitメソッドの使用も推奨されています。これについてはドキュメントを参照してください(初めて使うときにはギョッとするかもしれません)。
今回はカリフォルニア州の住宅価格データセットを例に単回帰分析を行うコードを紹介しました。次回はガラッと話題を変えて日付の扱いを取り上げる予定です。
Copyright© Digital Advantage Corp. All Rights Reserved.

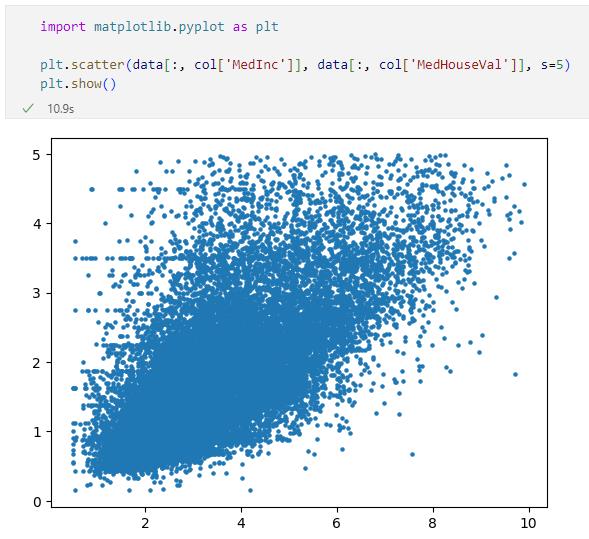 前回作成した散布図
前回作成した散布図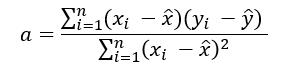
 傾きが2となるX座標とY座標の組みをプロットしたもの
傾きが2となるX座標とY座標の組みをプロットしたもの 実行結果
実行結果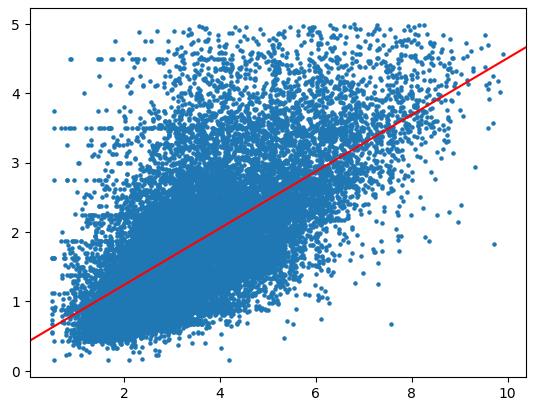 実行結果
実行結果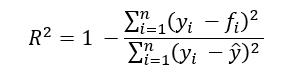
 実行結果
実行結果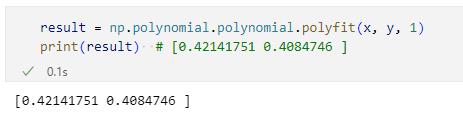 実行結果
実行結果



