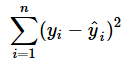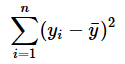［評価関数］決定係数（Coefficient of Determination）R2とは？：AI・機械学習の用語辞典

用語「決定係数R2（R二乗）」について説明。線形回帰モデルの評価関数の一つで、回帰式のモデルによる予測が観測データにどれくらい当てはまるかを表す。

» 2023年10月02日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

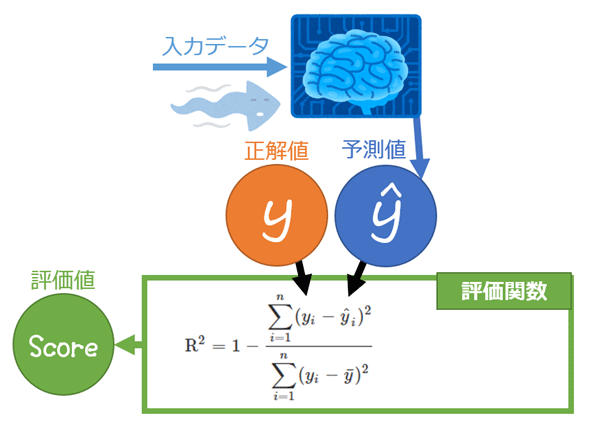
　統計学／機械学習における決定係数（Coefficient of Determination、寄与率）のR²（R squared）とは、主に単回帰分析／重回帰分析といった線形回帰（Linear Regression）*1における回帰式のモデルによる予測が「観測データ（正解データ）*2にどれくらい当てはまるか」の割合（通常は0～1.0＝100％、マイナスになることもある）を出力する関数である（図1）。

*1　統計学に基づく線形回帰モデルに入力する各種データは「説明変数」や「独立変数」と呼ばれ、これが機械学習での「入力データ」となる「特徴量」に相当する。また線形回帰モデルでは、モデルから出力される「予測値」は「目的変数」や「従属変数」と呼ばれる。本稿の趣旨から逸脱するのでごく簡略的に示すと、線形回帰のモデルは、説明変数（例えばx₁とx₂）と目的変数（例えばy）を用いてy＝ax₁＋bx₂＋cのような式で表現でき、最適化によってパラメーターa／b／cを決定する。

*2　機械学習で「（教師）ラベル」や「正解値」などと呼ぶものは、統計学においては「観測値（observed value）」や「実測値」「実際の測定値」などと呼ばれることが一般的である。

図1　「決定係数R2」のイメージ

定義と数式

　R²の値は一般的に、1（＝100％）から「残差平方和÷全平方和」（0以上）を引く計算式で算出される（※ちなみに詳細は割愛するが、この計算式以外にも微妙に異なるさまざまな計算式がある）。下に前述の計算式を示すが、今回は式が複雑そうに見えるのと見慣れない用語が幾つか出ていると思うので、式の部分ごとに分けてどういう意味かを以下で説明していく。

　残差変動とは、観測データ（正解データ）がモデルの予測からどれくらいズレているかを示す数値である（数値が大きいほどズレていることになる）。残差変動は、各データに対して「観測値と予測値の差（＝残差）」*3を二乗した値を総和する計算（＝残差平方和、「平均していない二乗誤差」と同じ計算式）で得られる。

*3　ここでいう「残差（residual）」とは、平均二乗誤差など他の評価関数では「正解値と予測値との差（＝誤差：error）」と説明したものと同じものである。

　この残差変動を全変動における割合値にするために、上記の数式では「残差平方和を全平方和で割って」いる。

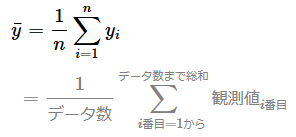
　全変動とは、観測データ（正解データ）自体の平均からのバラツキ具合を示す数値である。全変動は、各データに対して「観測値と全観測データの平均値との差」を二乗した値を総和する計算（＝全平方和、「平均していない分散」と同じ計算式）で得られる。

自由度調整済み決定係数について

　R²は説明変数（特徴量）の数が増えるほど、1.0に近づく性質がある。その問題を回避するために、自由度調整済み決定係数（Adjusted Coefficient of Determination、Adjusted R²）というR²の応用バージョンがある。この評価指標は、統計ツールの出力結果などでよく見るので、統計処理では広く使われていると考えられる。機械学習ライブラリのscikit-learnには、R²基本バージョンしか搭載されていないので、本稿でも以下に式を示すだけにとどめる。残差平方和がn－k－1で割られ、全平方和がn－1で割られるのがポイントである。kは説明変数の数で、（R²の式にもあった）nはデータ数（サンプルサイズ）である。