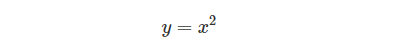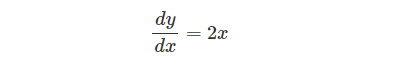第1回 難しくない! PyTorchでニューラルネットワークの基本:PyTorch入門
PyTorchの習得は、シンプルなニューラルネットワーク(NN)の、まずは1つだけのニューロンを実装することから始めてみよう。ニューロンのモデル定義から始め、フォワードプロパゲーションとバックプロパゲーションといった最低限必要な「核」となる基本機能に絞って解説。自動微分についても簡単に触れる。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
人気急上昇の「PyTorch」を使いたい。そう考えて、PyTorchの公式チュートリアルを開いて学習を始めてみた、という人は少なくないだろう。しかし、挫折してしまったり、なかなか進まなかったり、という人も少なくないのではないだろうか。
というのも、その公式チュートリアルの、最初の「テンソル」解説だけは(NumPyライクな直観的なAPIなので)難しくないとしても、次が「Autograd(自動微分)」、その次が「ニューラルネットワーク」……と言いつつも、いきなり「CNN(畳み込みニューラルネットワーク)」による説明になっているからだ。ニューラルネットワークやディープラーニングの経験が浅い初心者にとって、そういった少しハイレベルな視点からの解説は、PyTorch機能そのものを学ぶ際の「理解の妨げ」になりやすいだろう。そもそも公式チュートリアルやAPIドキュメントが英語版しか提供されていない、という障壁もある(※ただし最近は、Chromeブラウザーが持つ[日本語に翻訳]機能が優秀なので、機械翻訳すれば十分に読めるが)。
PyTorchはわざと「入門の壁」を高くして、ある程度の知識がある人だけが入って来られるように「門前払い」しているのではないか。筆書はそんなふうにすら感じている。
PyTorchだって難しくない
しかしPyTorchはしょせん“ツール”に過ぎない。あくまでツールとして捉えて「PyTorchを活用するのは難しくない」と本連載では主張したい。
本連載の目的と方針
PyTorchは世界的な人気のわりには、日本語の分かりやすいチュートリアルがまだほとんどない。そこで本連載は、日本語によるチュートリアル入門記事として、できるだけシンプルなニューラルネットワークを題材にして、PyTorchでニューラルネットワークを活用するための最重要かつ最低限の基礎知識を最短で説明していく(※基本中の基本を本連載の第1回〜第3回の3本にまとめた)。
読者に想定するゴールとしては、PyTorchの基本的な実装パターンを理解し、初歩的なニューラルネットワーク&ディープラーニングのコードが思い通りに書けるようになること、としたい。
本連載の読者対象は、「ニューラルネットワークの基本を学んだことがあるレベル」を想定している。具体的には、連載『TensorFlow 2+Keras(tf.keras)入門』のうち、下記の「仕組み理解×初実装」の前編・中編・後編の3本を読んで、内容を理解している状態とする。
例えば「ニューロン」「活性化関数」「正則化」「勾配」「確率的勾配降下法(SGD)」と聞いて、「その概念が分からない」といった場合には、先に上記3本の記事に目を通してほしい。この3本の記事では、ニューラルネットワークの挙動を図で示しながら、仕組み(とKerasによる実装方法)を分かりやすく説明しているのでお勧めである。
本連載では、Python(バージョン3.6)と、ディープラーニングのライブラリ「PyTorch」の最新版1.4を利用する。また、開発環境にGoogle Colaboratory(以下、Colab)を用いる。
さっそく説明を始めよう!
PyTorchとは?
PyTorch(パイトーチ)とは、Facebookが開発しているオープンソースの機械学習(特にディープラーニング)のライブラリである。その代表的な特徴を3つだけ挙げるとすれば、以下の通りだ。
- 人気急上昇中: 参考記事「PyTorch vs. TensorFlow、ディープラーニングフレームワークはどっちを使うべきか問題」
- Pythonic: Pythonのイディオムをうまく活用した自然なコーディングが可能
- 柔軟性や拡張性に優れる: 「動的」に計算グラフ(=ライブラリ内部で計算処理に使うデータフローなどのグラフ)を構築できる
3番目が特に重要で、例えばモデルのフォワードプロパゲーション(順伝播)時にif条件やforループなどの制御フローを書くなどして動的に計算グラフを変更するといったことが可能だ。とりわけNLP(Natural Language Processing:自然言語処理)の分野では、研究者はさまざまな長さの文を訓練する必要があるので、「動的な計算グラフ」機能が必要不可欠である(※実際に筆者が「PyTorchがデファクトスタンダードになっている」と初めて聞いたのは、NLPの分野だった)。
「動的な計算グラフ」はもちろんPyTorch以外のライブラリにも搭載されており、他のライブラリでは“Define-by-Run”(実行しながら定義する)やEager Execution(即時実行)などとも呼ばれている。例えばTensorFlow 2.0以降にはEager Executionが搭載されたが、「動的な計算グラフ」の細かな使い勝手はPyTorchに一日の長がある(と筆者は感じている)。
本連載の第3回までで説明する大まかな流れ
本連載では、PyTorchの基礎を一気呵成(かせい)に習得していく。具体的には、次の流れで説明する。
(1)ニューロンのモデル定義
(2)フォワードプロパゲーション(順伝播)
(3)バックプロパゲーション(逆伝播)と自動微分(Autograd)
(4)PyTorchの基礎: テンソルとデータ型
(5)データセットとデータローダー(DataLoader)
(6)ディープニューラルネットのモデル定義
(7)学習/最適化(オプティマイザ)
(8)評価/精度検証
(1)〜(3)が1セットで、1つのニューロンだけのネットワークを題材に、PyTorchの核となる部分を説明する。これが第1回(本稿)。
(4)は、より本格的にPyTorchによるディープラーニングの手順を学ぶに当たり、PyTorchの基礎部分(テンソルとデータ型)をチートシート形式でざっと確認していただく。これが第2回。
(5)〜(8)が再び1セットで、4層のディープニューラルネットワークを題材に、PyTorchによる基本的な実装と一連の流れを解説する。これが第3回である。
第3回までのタイトルは下記のようになっている。
- 第1回: 難しくない! PyTorchでニューラルネットワークの基本(今回)
- 第2回: PyTorchのテンソル&データ型のチートシート
- 第3回: PyTorchによるディープラーニング実装手順の基本
全部読み通すとかなりのボリュームになっているが、頑張って最後まで付いてきてほしい。
(1)ニューロンのモデル定義
それでは、「ニューロン」の入力と出力を行うコードをPyTorchで記述してみよう。
PyTorch 1.4のインストール
本連載では、PyTorchのバージョン1.4以上を必須とする(※Colabにインストール済みのPyTorchバージョンが分からない場合は、import torch; print('PyTorch', torch.__version__)を実行すれば、バージョンを確認できる)。
本連載が利用を前提とするColabにデフォルトでインストール済みのバージョンは、(2020年2月4日執筆時点で)PyTorch 1.4.0だった。バージョンが1.4以上ではない場合は、ライブラリ「torch」を最新版にアップグレードして使う必要がある。
そのためには、リスト1-0に示すいずれかのコードを実行して、アップグレード(もしくはインストール)する。実行後に、[RESTART RUNTIME]ボタンが表示されるので、クリックしてランタイムを再起動してほしい。
#!pip install torch # ライブラリ「PyTorch」をインストール
#!pip install torchvision # 画像/ビデオ処理のPyTorch用追加パッケージもインストール
# 最新バージョンにアップグレードする場合
!pip install --upgrade torch torchvision
# バージョンを明示してアップグレードする場合
#!pip install --upgrade torch===1.4.0 torchvision===0.5.0
# 最新バージョンをインストールする場合
#!pip install torch torchvision
# バージョンを明示してインストールする場合
#!pip install torch===1.4.0 torchvision===0.5.0
リスト1-0では、「torchvision」パッケージもアップグレード(もしくはインストール)しているが、本連載では使っていない。しかし同時にインストールしておかないと、パッケージ関係が不整合になるため、ここでインストールしておく必要がある。
ニューロンのモデル設計と活性化関数
PyTorchの利用環境が整ったとして話を進めよう。ここでは、2つの入力を受け付けて、それを使った計算結果を1つの出力として生成するニューロンを、モデル化(=モデル設計)する。
モデル設計のために、ライブラリ「PyTorch」のメインパッケージであるtorchをインポートし、その中で定義されているnnパッケージ(=NN:ニューラルネットワーク機能)を使って、torch.nn.Moduleクラスを継承した「独自の派生クラス」(今回の名前は「NeuralNetwork」)を作成する。なお、torch.nn.Moduleを「モジュール」と記載すると、Pythonの「モジュール」と紛らわしいので、本連載では「torch.nn.Module」で表記を統一する。
ちなみにPyTorchによるモデルの作成方法/書き方は幾つかあり、代表的なものを挙げるなら以下の3つである。
- torch.nn.Moduleクラスのサブクラス化: これから説明する。典型的な書き方なので、最もお勧めできる
- torch.nn.Sequentialクラス: 確かにKerasのようにシンプルに書けるが、PyTorchの良さがなくなる
- 低水準APIを使ってフルスクラッチ実装: 高水準APIのtorch.nn.Moduleを使う方が、効率がよい
モデル設計のコードは、リスト1-1のようになる。ちなみにPyTorchでは、インデントのタブ文字数は4となっているので、本連載ではそれに従うこととする。ここでは何らかの座標を入力すると(2つの入力値)、それが青色なのかオレンジ色なのか(1つの出力値)を推測するものとする(青:1.0〜オレンジ:-1.0の範囲)。
import torch # ライブラリ「PyTorch」のtorchパッケージをインポート
import torch.nn as nn # 「ニューラルネットワーク」モジュールの別名定義
# 定数(モデル定義時に必要となるもの)
INPUT_FEATURES = 2 # 入力(特徴)の数: 2
OUTPUT_NEURONS = 1 # ニューロンの数: 1
# 変数(モデル定義時に必要となるもの)
activation = torch.nn.Tanh() # 活性化関数: tanh関数
# 「torch.nn.Moduleクラスのサブクラス化」によるモデルの定義
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
# 層(layer:レイヤー)を定義
self.layer1 = nn.Linear( # Linearは「全結合層」を指す
INPUT_FEATURES, # データ(特徴)の入力ユニット数
OUTPUT_NEURONS) # 出力結果への出力ユニット数
def forward(self, input):
# フォワードパスを定義
output = activation(self.layer1(input)) # 活性化関数は変数として定義
# 「出力=活性化関数(第n層(入力))」の形式で記述する。
# 層(layer)を重ねる場合は、同様の記述を続ければよい(第3回)。
# 「出力(output)」は次の層(layer)への「入力(input)」に使う。
# 慣例では入力も出力も「x」と同じ変数名で記述する(よって以下では「x」と書く)
return output
# モデル(NeuralNetworkクラス)のインスタンス化
model = NeuralNetwork()
model # モデルの内容を出力
コード内にできるだけ多くの説明コメントを入れたので、本文ではポイントのみを示すこととしよう。
まずclass NeuralNetwork(nn.Module):が、「torch.nn.Moduleクラスのサブクラス化」の部分である。クラス内には、
- __init__関数: レイヤー(層)を定義する
- forward関数: フォワードパス(=活性化関数で変換しながらデータを流す処理)を実装する
の2つのメソッドが実装されている。NeuralNetworkクラスをインスタンス化すればモデルの作成は完了だ。
レイヤー(層)を定義しているtorch.nn.Linearクラスは、「入力データに対して線形変換を行うこと」を意味し、一般的には全結合層(Fully Connected Layer)と呼ばれており、ライブラリによっては「Dense層」(Kerasなど)や「Affine層」(Neural Network Consoleなど)とも呼ばれている。Linearクラスのコンストラクター(厳密には__init__関数)の第1引数と第2引数には、入力ユニット数と出力ユニット数を指定すればよい。
活性化関数は、activation変数に定義しているが、今回はtanh関数(図1-1)を使用する。
PyTorchでは、活性化関数としてtorch.nnパッケージ内に以下のものが用意されており、すぐに利用できる(※カッコ書きがあるものは特に有名なもの)。
- ELU
- Hardshrink
- Hardtanh
- LeakyReLU
- LogSigmoid
- MultiheadAttention
- PReLU
- ReLU(有名)
- ReLU6
- RReLU
- SELU
- CELU
- GELU
- Sigmoid(シグモイド)
- Softplus(ソフトプラス)
- Softshrink
- Softsign(ソフトサイン)
- Tanh(本連載で使用)
- Tanhshrink
- Threshold
- Softmin
- Softmax(ソフトマックス)
- Softmax2d
- LogSoftmax
- AdaptiveLogSoftmaxWithLoss
パラメーター(重みとバイアス)の初期値設定
「パラメーター(=重みとバイアス)を初期化したい」というニーズは高いだろう。例えば「0」や「一様分布のランダム値」で初期化するなどの方法がある。この方法については、第3回で掲載するリスト7-4の冒頭で示す。
ここでは「自動的な初期化」ではなく「任意の初期値の指定」を行う方法を説明する。初期値の例として、2つの入力(の接続線)にかかる重みに「0.6」と「-0.2」を、バイアスには「0.8」を設定することにしよう(リスト1-2)。
# パラメーター(ニューロンへの入力で必要となるもの)の定義
weight_array = nn.Parameter(
torch.tensor([[ 0.6,
-0.2]])) # 重み
bias_array = nn.Parameter(
torch.tensor([ 0.8 ])) # バイアス
# 重みとバイアスの初期値設定
model.layer1.weight = weight_array
model.layer1.bias = bias_array
# torch.nn.Module全体の状態を辞書形式で取得
params = model.state_dict()
#params = list(model.parameters()) # このように取得することも可能
params
# 出力例:
# OrderedDict([('layer1.weight', tensor([[ 0.6000, -0.2000]])),
# ('layer1.bias', tensor([0.8000]))])
リスト1-2もポイントを示しておこう。
モデルのパラメーターはtorch.nn.Parameterオブジェクトとして定義する必要がある。そのtorch.nn.Parameterクラスのコンストラクターには、torch.Tensorオブジェクト(以下、テンソル)を指定する(※テンソルの使い方の詳細は、第2回で説明する)。そのtorch.Tensorクラスのコンストラクターには、Pythonの多次元リストを指定できる。このクラスを活用して、重みとバイアスをweight_arrayとbias_arrayという変数に定義している。
定義した重みやバイアスをモデルに適用するには、
- <モデル名>.<レイヤー名>.weightプロパティ: 重みを指定可能
- <モデル名>.<レイヤー名>.biasプロパティ: バイアスを指定可能
を使用すればよい。
重みやバイアスといったパラメーターの情報を取得して表示したい場合には、<モデル名>.state_dict()メソッドが便利だ。このメソッドを使えば、パラメーターといったtorch.nn.Module全体の状態が取得できる。
ちなみに情報取得ではなく、最適化のために使う「実際のパラメーターのオブジェクト」を取得するには、<モデル名>.parameters()メソッドを呼び出せばよい。この方法については、第3回に掲載するリスト7-1で示す。
(2)フォワードプロパゲーション(順伝播)
以上でモデルの設計は完了だ。実際にサンプルデータを入力してフォワードプロパゲーションを実行し、その出力結果を確認してみよう。
フォワードプロパゲーションの実行と結果確認
フォワードプロパゲーション、つまりモデルによる推論/予測は、modelオブジェクトを関数のように呼び出すだけである(厳密には__call__メソッドの呼び出し)。この関数の引数には、(テンソルの)入力値を渡せばよい。戻り値として、出力結果(つまり予測値)がテンソル値で返される。
それを実際に行っているのがリスト2-1である。
X_data = torch.tensor([[1.0, 2.0]]) # 入力する座標データ(1.0、2.0)
print(X_data)
# tensor([[1., 2.]]) ……などと表示される
y_pred = model(X_data) # このモデルに、データを入力して、出力を得る(=予測:predict)
print(y_pred)
# tensor([[0.7616]], grad_fn=<TanhBackward>) ……などと表示される
リスト2-1のポイントを示す。
フォワードプロパゲーション(順伝播)により、座標データ「1.0、2.0」(X_data)の入力から、モデル(model)が推論した結果(y_pred)が出力されている。その結果の数値は、手動で計算した値(0.7616)と同じになることが確認できるはずだ(計算内容は、前述の記事「中編: ニューラルネットワーク最速入門」で説明しているので、本連載では割愛する)。
出力結果のテンソルに含まれるgrad_fn属性(この例では「TanhBackward」)には、勾配(gradient、=偏微分: partial derivative)を計算するための関数(fn: function)が自動作成されている。この関数はバックプロパゲーション(逆伝播)による学習の際に、モデル内部で暗黙的に利用される。
動的な計算グラフの可視化
以上で、ニューロンのモデルが正常に設計できていることが確認できた。ではその中の構造、つまり計算グラフがどのようになっているのかが気になるのではないだろうか。その内容を画像にして可視化することもできるので、やってみよう。
動的な計算グラフ(dynamic computation graph)を手軽に可視化するには、非公式のツールを使う必要がある。具体的には「torchviz」というツールが便利である。これをpipなどでインストールして使ってみたのが、リスト2-2である。
from torchviz import make_dot # 「torchviz」モジュールから「make_dot」関数をインポート
make_dot(y_pred, params=dict(model.named_parameters()))
# 引数「params」には、全パラメーターの「名前: テンソル」の辞書を指定する。
# 「dict(model.named_parameters())」はその辞書を取得している
リスト2-2を実行すると、図2-1のような画像が生成される。
図2-1の色分けの意味は以下の通り。矢印によりデータフローも分かるようになっている。
- 青色のボックス: 勾配を計算する必要があるパラメーター(重みやバイアスなど)。この例では(1, 2)が重みで、(1)がバイアス
- 灰色のボックス: 勾配(偏微分)などを計算するための関数。関数(この例では「TBackward」や「AddmmBackward」)は「テンソル」データのgrad_fn属性に自動作成されている
- 緑色のボックス: グラフ計算の開始点。backward()メソッド(後述)を呼び出すと、ここから逆順に計算していく。内容は灰色のボックスと同じ
(3)バックプロパゲーション(逆伝播)と自動微分(Autograd)
フォワードプロパゲーション(順伝播)の説明が終わった。可視化の説明でbackward()メソッドも登場したので、次にバックプロパゲーション(逆伝播)と、その内部で働く「自動微分」についても説明しておこう(※非常に簡単な話しか書かないので、心配しなくて大丈夫である)。
簡単な式で自動微分してみる
PyTorchでは、backward()メソッドを呼び出すと、バックプロパゲーション(Back-propagation:Backprop、誤差逆伝播)が行われる。ニューラルネットワークの誤差逆伝播では、「微分係数(derivative)の計算」という面倒くさい処理が待っている。ディープラーニングのライブラリは、この処理を自動化してくれるので大変便利である。この機能を「自動微分(AD: Automatic differentiation)」や「Autograd」(gradients computed automatically: 自動計算された勾配)などと呼ぶ*1。
*1 ちなみに詳細を知る必要はあまりないが、torch.autogradモジュールは、厳密には「リバースモードの自動微分」機能を提供しており、Vector-Jacobian Product(VJP: ベクトル-ヤコビアン積)と呼ばれる計算を行うエンジンである(参考「Autograd: Automatic Differentiation — PyTorch Tutorials 1.4.0 documentation」、論文「Automatic differentiation in PyTorch | OpenReview」)。
PyTorchの自動微分(Autograd)機能を、いったんニューロンのモデルから離れて、非常にシンプルな例で確認してみよう。
ここでは、
という計算式を微分することとする。yをxで微分する導関数(derivative function)は、
となる(「xの二乗」の導関数は、二乗から係数として「2」が前に出て、二乗の指数は「-1」されて「x」となる。その結果、2xが算出される)。
この導関数で計算した結果、つまり微分係数(derivative=接線の傾き)は、勾配(gradient)を意味する。よって、例えばxが1.0の地点の勾配は2.0となる。ちなみにバックプロパゲーション&最適化では、この勾配に学習率を掛けて、パラメーターの数値をちょっとずつ更新していくのである。
この微分計算を、PyTorchのbackward()メソッドを使って自動的に行うと、リスト3-1のようになる。
x = torch.tensor(1.0, requires_grad=True) # 今回は入力に勾配(gradient)を必要とする
# 「requires_grad」が「True」(デフォルト:False)の場合、
# torch.autogradが入力テンソルに関するパラメーター操作(勾配)を記録するようになる
#x.requires_grad_(True) # 「requires_grad_()」メソッドで後から変更することも可能
y = x ** 2 # 「yイコールxの二乗」という計算式の計算グラフを構築
print(y) # tensor(1., grad_fn=<PowBackward0>) ……などと表示される
y.backward() # 逆伝播の処理として、上記式から微分係数(=勾配)を計算(自動微分:Autograd)
g = x.grad # 与えられた入力(x)によって計算された勾配の値(grad)を取得
print(g) # tensor(2.) ……などと表示される
# 計算式の微分係数(=勾配)を計算するための導関数は「dy/dx=2x」なので、
#「x=1.0」地点の勾配(=接線の傾き)は「2.0」となり、出力結果は正しい。
# 例えば「x=0.0」地点の勾配は「0.0」、「x=10.0」地点の勾配は「20.0」である
リスト3-1の最終出力を見ると、2.0となっており、「自動微分」機能の実行が確認できたことになる。
入力xのテンソルの作成でrequires_grad=Trueという記述がある。通常の「torch.nn.Moduleクラスのサブクラス化」したモデルでは、各パラメーターのテンソルに勾配が保存(蓄積)される仕組みになっている(後述)。しかしこの例では、y = x ** 2という計算式がモデルであるため、変数となるテンソルxに勾配が保存されるように明示的に指定しなければならない、というわけだ。
出力されたテンソル(y)のbackward()メソッドで、バックプロパゲーション(逆伝播)を実行できる。ちなみにニューラルネットワークの場合は、損失(loss)を表すテンソルのbackward()メソッドを呼び出すことになる。
自動微分が行われた結果、計算された微分係数(=勾配)は、入力したテンソルのgradプロパティで取得できる。
ニューラルネットワークにおける各パラメーターの勾配
自動微分を手元で確認できた。再び、ニューロンのモデルに話を戻し、今度は損失を表すテンソル(loss)のbackward()メソッドを呼び出してみよう(リスト3-2)。
# 勾配計算の前に、各パラメーター(重みやバイアス)の勾配の値(grad)をリセットしておく
model.layer1.weight.grad = None # 重み
model.layer1.bias.grad = None # バイアス
#model.zero_grad() # これを呼び出しても上記と同じくリセットされる
X_data = torch.tensor([[1.0, 2.0]]) # 入力データ(※再掲)
y_pred = model(X_data) # 出力結果(※再掲)
y_true = torch.tensor([[1.0]]) # 正解ラベル
criterion = nn.MSELoss() # 誤差からの損失を測る「基準」=損失関数
loss = criterion(y_pred, y_true) # 誤差(出力結果と正解ラベルの差)から損失を取得
loss.backward() # 逆伝播の処理として、勾配を計算(自動微分:Autograd)
# 勾配の値(grad)は、各パラメーター(重みやバイアス)から取得できる
print(model.layer1.weight.grad) # tensor([[-0.2002, -0.4005]]) ……などと表示される
print(model.layer1.bias.grad) # tensor([-0.2002]) ……などと表示される
# ※パラメーターは「list(model.parameters())」で取得することも可能
「損失(loss)」は、まず出力結果と正解ラベルの「誤差(error)」を損失関数(この例では「平均二乗誤差:MSE」、詳細は第3回の「リスト7-2 損失関数の定義」を参照)で変換して算出する。
リスト3-2では、変数criterionに代入されたnn.MSELoss()がその損失関数である(※PyTorchで使える損失関数については第3回で説明する)。損失関数はcriterionという名前の変数に代入するのが定石となっている。
損失関数で計算された「損失(loss)」を使ってバックプロパゲーションを行うために、loss.backward()メソッドを呼び出している。
計算された勾配の値は、モデル内に存在する各パラメーター(weightやbias)に蓄積されており、そのgradプロパティから取得できる。
なお、この例では単純にするために1回しかバックプロパゲーションを実行していないが、本来はミニバッチのイテレーション単位(もしくは全体のエポック単位)で繰り返しバックプロパゲーションしながら、パラメーターの最適化を進めていく(第3回の『リスト7-3 1回分の「訓練(学習)」と「評価」の処理』と『リスト7-4 「訓練」と「評価」をバッチサイズ単位でエポック回繰り返す』で、より具体的に説明する)。
以上で、PyTorchの核となる部分の説明が終わった。まずはここまでを確実にマスターしてほしい。
次回は、PyTorchの基礎部分といえる「テンソルとデータ型」をチートシート形式で確認する。
Copyright© Digital Advantage Corp. All Rights Reserved.

 図0-1 あい博士「PyTorchだって難しくない!」、マナブくん「ホントに?」
図0-1 あい博士「PyTorchだって難しくない!」、マナブくん「ホントに?」

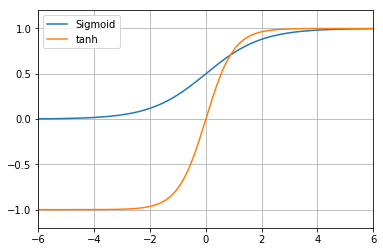 図1-1 tanh関数(参考比較対象:シグモイド関数)
図1-1 tanh関数(参考比較対象:シグモイド関数)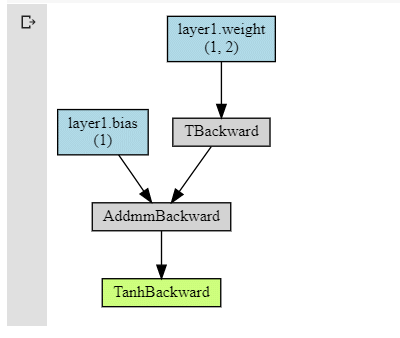 図2-1 動的な計算グラフの画像例
図2-1 動的な計算グラフの画像例